Autor: Lukáš Gáborik, [email protected]

Letná škola matematiky 2023

Teória

Hodnoty zachovávané zobrazeniami

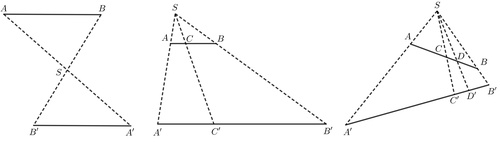
Určite viete, že stredová súmernosť zachováva dĺžky $-$ teda, ak sa úsečka $AB$ zobrazí v stredovej súmernosti na $A'B'$, tak $|AB|=|A'B'|$.

Stredová súmernosť je len špecifickým prípadom rovnoľahlosti (ide o rovnoľahlosť s koeficientom $-1$). Pri rovnoľahlosti sa síce nezachovávajú dĺžky, no zachováva sa ich pomer.

Uvedomte si, že vďaka orientovaným dĺžkam je deliaci pomer záporný, keď $C$ leží vnútri úsečky $AB$ a kladný, keď leží mimo tejto úsečky.

Aj rovnoľahlosť je však len špeciálnym prípadom iného typu zobrazení. Ide o takzvané projektívne zobrazenia, ktoré „premietajú“ body z jednej priamky na druhú (rovnoľahlosť má navyše podmienku, že tieto priamky musia byť rovnobežné). Mohlo by nás zaujímať, aká hodnota sa zachováva pri projekcii. No a tak, ako sme medzi stredovou súmernosťou prešli medzi absolútnymi hodnotami a relatívnym pomerom dĺžok, tak tu prejdeme medzi absolútnymi hodnotami a relatívnym pomerom deliaceho pomeru.

Uvedomte si, že dvojpomer nadobúda záporné hodnoty, keď jeden z bodov $C, D$ je vnútri úsečky $AB$ a druhý mimo nej. Kladné hodnoty nadobúda inak. Teraz by sme sa chceli naozaj presvedčiť, že projekcia zachováva dvojpomer. Poďme teda na to.

Veta

Nech $a, b, c, d$ sú priamky prechádzajúce jedným bodom $S$ a nech priamka $p$ ich pretína postupne v bodoch $A, B, C, D$. Potom hodnota dvojpomeru $(ABCD)$ nezávisí od voľby priamky $p$.

Dôkaz

Najskôr sa pozrieme na absolútne hodnoty a nebudeme riešiť znamienko. Potom sa zamyslíme, že aj znamienko zostane rovnaké.

Rozpíšme si dvojpomer ako $$(ABCD)=\frac{(ABC)}{(ABD)}=\frac{\frac{|AC|}{|BC|}}{\frac{|AD|}{|BD|}}=\frac{|AC|\cdot|BD|}{|BC|\cdot|AD|}.$$ Nech $[XYZ]$ značí obsah trojuholníka $XYZ$. Keby sme uvedené dĺžky vynásobili výškou $v$ a vydelili dvomi, dostali by sme obsahy nejakých trojuholníkov. Opačne preto ale $$(ABCD)=\frac{|AC|\cdot|BD|}{|BC|\cdot|AD|}=\frac{\frac{2[SAC]}{v}\cdot\frac{2[SBD]}{v}}{\frac{2[SBC]}{v}\cdot\frac{2[SAD]}{v}}=\frac{[SAC]\cdot[SBD]}{[SBC]\cdot[SAD]}.$$

Teraz už len využime vzťah, ktorý nám umožňuje vypočítať obsah trojuholníka cez dĺžky jeho dvoch strán a uhol nimi zovretý. Potom $$(ABCD)=\frac{[SAC]\cdot[SBD]}{[SBC]\cdot[SAD]}=\frac{\frac{|SA|\cdot|SC|\cdot\sin\alpha}{2}\cdot\frac{|SB|\cdot|SD|\cdot\sin\gamma}{2}}{\frac{|SB|\cdot|SC|\cdot\sin(\beta+\gamma)}{2}\cdot\frac{|SA|\cdot|SD|\cdot\sin(\alpha+\beta)}{2}}=\frac{\sin\alpha\sin\gamma}{\sin(\alpha+\beta)\sin(\beta+\gamma)}.$$ Dvojpomer $(ABCD)$ sa nám podarilo vyjadriť len vzhľadom na uhly medzi priamkami $a, b, c, d$, a preto absolútna hodnota dvojpomeru nezávisí od voľby priamky $p$.

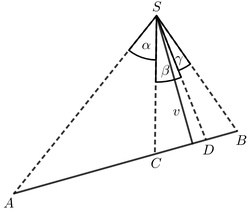
Pri voľbe inej priamky sa poradie bodov buď nezmení alebo cyklicky otočí. Môžete si premyslieť, že cyklickým otočením sa nezmení vlastnosť, či je jeden bod vnútri a druhý bod vonku, teda aj znamienko sa zachováva.

Harmonický štvorpomer

Ukazuje sa, že je zaujímavé skúmať niektoré konkrétne hodnoty dvojpomeru.

Základné konfigurácie

Os uhla a pravý uhol

Veta

Ak pre body $A,\ B,\ C,\ D$ na priamke a $P$ mimo nej platia dve z nasledovných vlastností, platí pre ne aj tá tretia:

1. $A,\ B,\ C,\ D$ sú v harmonickom štvorpomere,
2. $|\sphericalangle APB|=90^\circ$,
3. $|\sphericalangle CPB|=|\sphericalangle BPD|$.

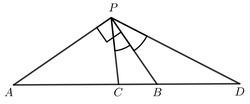
Dôkaz

Podobne ako v predošlom dôkaze vieme vyjadriť hodnotu absolútnej hodnoty dvojpomeru ako $$|(ABCD)| = \frac{\sin\sphericalangle APC\cdot\sin\sphericalangle BPD}{\sin\sphericalangle BPC\cdot\sin\sphericalangle APD}.$$ Štyri rôzne body nemôžu mať dvojpomer rovný plus jednej, preto môžeme tvrdiť, že štyri rôzne body ležia v harmonickom štvorpomere práve vtedy, keď absolútna hodnota štvorpomeru je rovná jednej.

2. + 3. $\Rightarrow$ 1.

Ak platí, že $|\sphericalangle APB|=90^\circ$ a $|\sphericalangle CPB|=|\sphericalangle BPD|$, potom sa hodnota dvojpomeru zjednoduší ako \begin{align} |(ABCD)| &= \frac{\sin\sphericalangle APC\cdot\sin\sphericalangle BPD}{\sin\sphericalangle BPC\cdot\sin\sphericalangle APD}=\frac{\sin\sphericalangle APC}{\sin\sphericalangle APD}=\frac{\sin\sphericalangle APC}{\sin(90^\circ+\sphericalangle BPD)}= \newline &=\frac{\sin\sphericalangle APC}{\sin(90^\circ-\sphericalangle BPD)}=\frac{\sin\sphericalangle APC}{\sin(90^\circ-\sphericalangle BPC)}=1. \end{align} Preto body $A, B, C, D$ ležia v harmonickom štvorpomere. Podobne sa dajú ukázať aj zvyšné dve implikácie.

Bod v nekonečne

Veta

Nech z bodu $P$ vychádza harmonický zväzok. Uvažujme priamku $a$ neprechádzajúcu bodom $P$ a jej priesečníky s troma priamkami harmonického zväzku označme postupne $A,\ B,\ C$. Potom $C$ je stredom úsečky $AB$ práve vtedy, keď štvrtá priamka harmonického zväzku je rovnobežná s priamkou $a$.

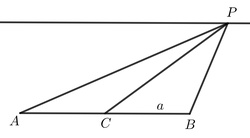
Dôkaz

Pre spor predpokladajme, že $C$ je stredom $AB$ a štvrtá priamka zväzku nie je rovnobežná s $a$. Potom existuje ich priesečník $D$. Keďže ide o harmonický zväzok, tento musí spĺňať $|AD|=|BD|$ a navyše $D$ musí byť mimo úsečky $AB$, aby sedelo znamienko. To je však spor. Opačná implikácia sa dá ukázať obdobne.

Tri priamky v jednom bode

Veta

Majme trojuholník $ABC$. Nech $A', B', C'$ sú body postupne na priamkach $BC, CA, AB$ také, že $AA',\ BB',\ CC'$ sú priamky pretínajúce sa v jednom bode (tiež známe ako Ceviány) a $|A'B|\neq|A'C|$. Označme $D=BC\cap B'C'$. Potom $B,\ C,\ A',\ D$ sú v harmonickom štvorpomere.

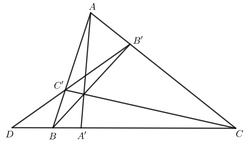
Dôkaz

Keďže $AA', BB', CC'$ sa pretínajú v jednom bode, z Cevovej vety vieme, že $$|BA'|\cdot|CB'|\cdot|AC'|=|CA'|\cdot|AB'|\cdot|BC'|.\tag{1}$$ Podobne, keďže $B', C', D$ ležia na priamke, z Menelaovej vety vyplýva, že $$|BD|\cdot|CB'|\cdot|AC'|=|CD|\cdot|AB'|\cdot|BC'|.\tag{2}$$ Spojením týchto dvoch tvrdení dostávame, že $$|(BCA')|=\frac{|BA'|}{|CA'|}\stackrel{(1)}{=}\frac{|AB'|\cdot|BC'|}{|CB'|\cdot|AC'|}\stackrel{(2)}{=}\frac{|BD|}{|CD|}=|(BCD)|,$$ a teda $|(BCA'D)|=1$, čo už vieme, že nám stačí.

Dve štvorice so spoločným bodom

Veta

Nech $A, C, B, D$ a $A, C', B', D'$ sú harmonické štvorice. Potom $BB'$, $CC'$, $DD'$ sú buď po dvoch rovnobežné, alebo sa pretínajú v jednom bode.

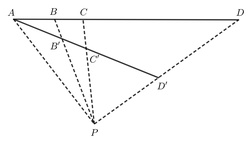
Dôkaz

Keď sú $BB', CC', DD'$ rovnobežné, tvrdenie platí. Preto uvažujme, že nejaká dvojica z nich (BUNV $BB'$, $CC'$) sú rôznobežné a pretínajú sa v bode $P$. Premietnime harmonickú štvoricu $ACBD$ cez $P$ na druhú z priamok. Dostaneme tak $AC'B'D''$, kde $D''$ je priesečník $DP$ a $AC'$. Avšak, keďže z troch bodov harmonickej štvorice je štvrtý jednoznačne určený, tak $D'=D''$. Preto aj $DD'$ prechádza $P$.

Úlohy

Úloha $1$

Majme trojuholník $ABC$, v ktorom si vyznačíme nasledovné body:

• stred vpísanej kružnice ako $I$,
• stred kružnice pripísanej ku strane $a$ ako $E_a$ a
• priesečník osi $\sphericalangle BAC$ a strany $a$ ako $D$.

Uistite sa, že $A, I, D, E_a$ ležia na jednej priamke. Následne dokážte, že tieto body ležia v harmonickom štvorpomere.

Úloha $2$

V trojuholníku $ABC$ označme päty výšok $A_0,\ B_0,\ C_0$. Bod $H$ je ortocentrum a $K=AA_0\cap B_0C_0$. Dokážte, že $A,\ K,\ H,\ A_0$ tvoria harmonickú štvoricu.

Táto úloha sa dá vyriešiť harmonickým štvorpomerom dvoma spôsobmi. Skúste nájsť oba.

Úloha $3$

Je daný rovnobežník $ABCD$ a bod $E$ tak, že $AE\parallel BD$. Dokážte, že $AB,\ AC,\ AD,\ AE$ tvoria harmonický zväzok.

Úloha $4$

Na kružnici $k$ sú dané body $A,\ B,\ E$ tak, že $|AE|\neq|BE|$ a ani jedna z priamok $AE, BE$ nie je kolmá na $AB$. Dokážte, že priesečníky osi $AB$ s kružnicou $k$ a priamkami $AE,\ BE$ tvoria harmonickú štvoricu.

Úloha $5$

Majme trojuholník $ABC$ a na jeho stranách $BC$, $AC$, $AB$ body $D$, $E$, $F$ také, že $BC\not\parallel EF$ a priamky $AD$, $BE$, $CF$ sa pretínajú v jednom bode. Označme tento priesečník $P$. Ďalej označme $Q=BC\cap EF$, $R=AD\cap EF$, $S=CF\cap BR$ a $T=DF\cap BR$. Ukážte, že $QREF$, $APDR$, $CSPF$ a $BSRT$ sú harmonické štvorice.

Úloha $6$ (Výberové sústredenie MO 2022)

Majme rovnoramenný trojuholník $ABC$ so základňou $BC$. Bod $K$ leží vnútri trojuholníka $ABC$ na jeho výške z vrchola $A$. Na priamke $BK$ leží bod $L$ taký, že $AL\parallel BC$. Dokážte, že ak $KC\perp CL$, tak potom $L$ leží na osi vonkajšieho uhla $\sphericalangle ACB$.

Úloha $7$ (Sharygin geometry olympiad 2013)

V trojuholníku $ABC$ označme $D$ pätu osi uhla pri vrchole $A$ a $I_b$, $I_c$ stredy kružníc vpísaných trojuholníkom $ABD$, $ACD$. Nech $I_bI_c\not\parallel BC$. Ak $Q=BC\cap I_bI_c$, ukážte, že $|\sphericalangle DAQ|=90^\circ$.

Rozšírenie

Označme priesečníky $I_bI_c$ s $AB, AC$ postupne $M, N$. Ukážte, že $AD, BN, CM$ prechádzajú jedným bodom.

Úloha $8$ (Blanchet's Theorem)

Majme trojuholník $ABC$. Označme pätu výšky na stranu $BC$ ako $D$. Na úsečke $AD$ je daný bod $P$. Nech $X=BP\cap AC$, $Y=CP\cap AB$. Dokážte, že $|\sphericalangle XDA|=|\sphericalangle YDA|$.

Úloha $9$

Na priamke $p$ sú dané body $B,\ D,\ C$ (v tomto poradí), pričom $D$ nie je stredom úsečky $BC$. Dokážte, že všetky body $X$ také, že $XD$ je os uhla $BXC$, ležia na fixnej kružnici.

Úloha $10$

Majme trojuholník $ABC$ a na jeho stranách $BC$, $AC$, $AB$ body $D$, $E$, $F$ také, že $AD$, $BE$, $CF$ sa pretínajú v jednom bode. Označme tento priesečník $K$. Priamka $FD$ pretína priamku $BE$ v bode $X$, $P$ je stred úsečky $AK$ a $EP$ pretína priamku $AB$ v bode $Y$. Ukážte, že $XY\parallel AD$.

Úloha $11$ (KMS 42/L2/10)

Máme trojuholník $ABC$, v ktorom $|AC|\neq|BC|$. Kružnica jemu vpísaná má stred v bode $I$ a dotýka sa strán $BC,\ CA,\ AB$ postupne v bodoch $D,\ E,\ F$. Stred strany $AB$ je $M$. Kolmica z bodu $I$ na ťažnicu $CM$ sa pretína s priamkou $DE$ v bode $K$. Dokážte, že $CK$ a $AB$ sú rovnobežné.

Úloha $12$

Je daná kružnica $\omega$ so stredom $O$ a tetivou $AB$ neprechádzajúcou stredom. Bod $C$ leží na $\omega$ tak, že $AC$ rozpoľuje úsečku $OB$. Označme $D=AB\cap OC$ a $F=BC\cap AO$. Dokážte, že $|AF|=|CD|$.

Úloha $13$

Majme ostrouhlý trojuholník $ABC$ s ortocentrom $H$. Kružnica nad priemerom $AB$ pretína priamku $CH$ v bodoch $X, Y$ a kružnica nad priemerom $AC$ pretína priamku $BH$ v bodoch $Z,W$. Ukážte, že priamky $XZ$ a $WY$ sa pretínajú na priamke $BC$.

Úloha $14$ (IMO Shortlist 1995, úloha G3)

Je daný trojuholník $ABC$. Body dotyku kružnice vpísanej so stranami $BC$, $AC$, $AB$ označme postupne $D$, $E$, $F$. Nech $X$ je bod vnútri trojuholníka taký, že kružnica vpísaná trojuholníku $XBC$ sa dotýka jeho strán v bodoch $D$, $Y$ a $Z$. Ukážte, že $E$, $F$, $Y$ a $Z$ ležia na jednej kružnici.