2. úloha vzorové riešenie

Zadanie

V New Yorkskej letiskovej hale treba vymeniť dlaždice. Hala má tvar trojuholníka \( ABC\) a vnútri neho sa nachádza bod \(P\). Bodom \(P\) sú vedené tri priamky rovnobežné so stranami trojuholníka, ktoré rozdeľujú podlahu haly na menšie časti (ako na obrázku). Robotníci už odmerali plochy troch menších trojuholníkov: \(S_1 = 4\, \mathrm{cm}^2,\, S_2 = 9\, \mathrm{cm}^2\) a \(S_3 = 16\, \mathrm{cm}^2\). Zistite, aký je obsah celej podlahy \(ABC\), ktorú treba vydláždiť.

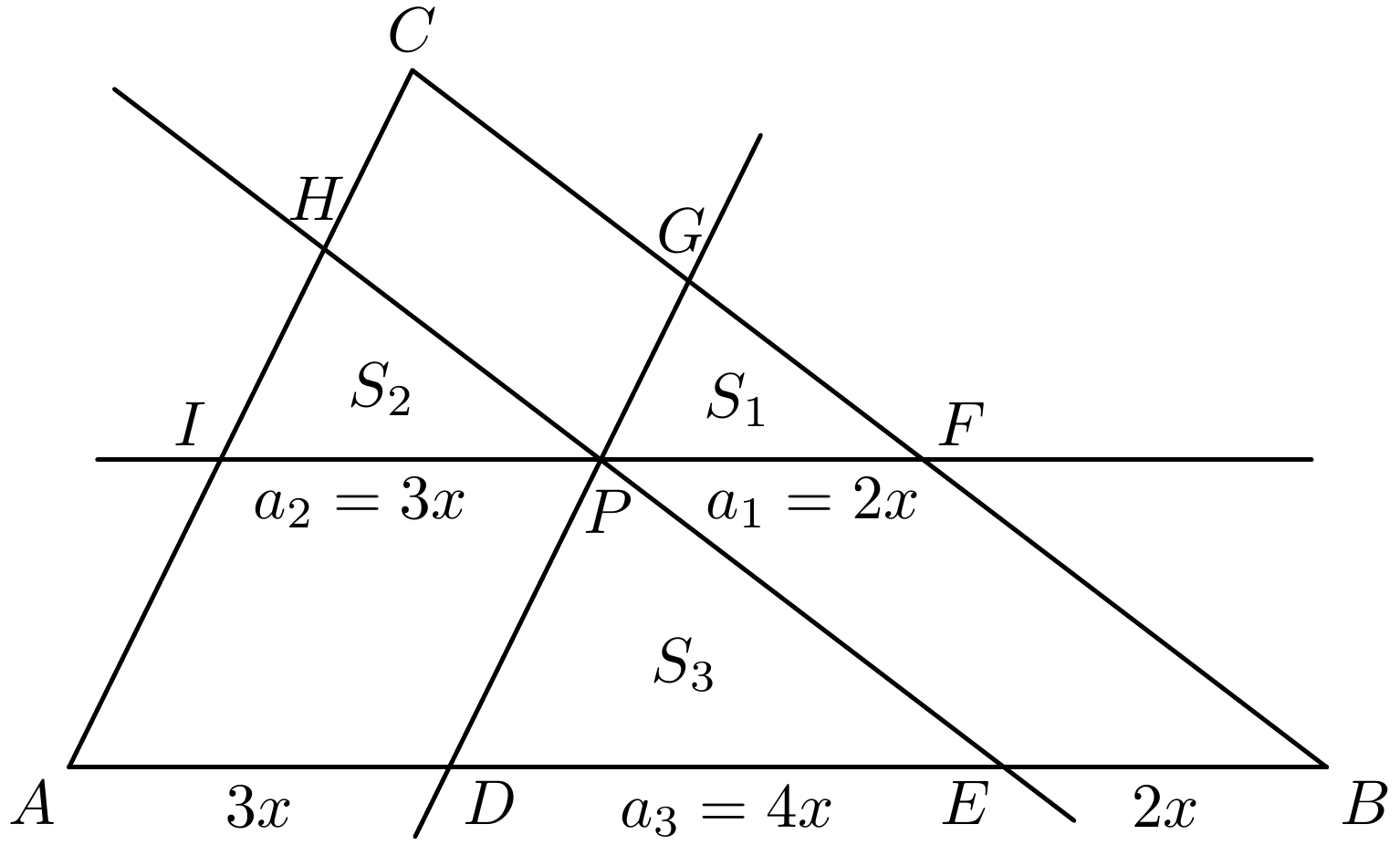
Ako prvé si všimneme, že všetky tri malé trojuholníky sú si navzájom podobné a zároveň sú podobné aj s veľkým trojuholníkom \(ABC\). Sú si podobné, pretože ich vnútorné uhly sú totožné s uhlami trojuholníka \(ABC\). Táto zhoda uhlov nie je náhodou, keď si zoberieme rovnobežku k ramenu uhla, tak vidíme, že uhol medzi druhým ramenom uhla a rovnobežkou je rovnaký ako pôvodný uhol.

Teraz dajme do vzťahu pomery obsahov a pomery strán trojuholníkov. Ak \(a\) a \(b\) sú strany podobných trojuholníkov, \(v_a\) a \(v_b\) sú výšky a \(k\) je koeficient podobnosti daných trojuholníkov tak platí:

\[k=\frac{a}{b}=\frac{v_a}{v_b}\] \[k^2=\frac{a\cdot v_a}{b \cdot v_b}=\frac{\frac{a \cdot v_a} {2}}{\frac{b\cdot v_b}{2}}=\frac{S_a}{S_b}\]

Z toho vyplýva, že ak je pomer strán trojuholníkov \(k\), potom pomer ich obsahov je \(k^2\). V našom príklade to použijeme na tri trojuholníky zo zadania:

\[S_1:S_2:S_3 = 4:9:16\] \[a_1:a_2:a_3 = 2:3:4\]

Z pomeru vieme, že dĺžky strán \(a_1\), \(a_2\) a \(a_3\) vieme nahradiť nejakým násobkom čísla \(x\) takto: \(a_1=2x\), \(a_2=3x\) a \(a_3 = 4x\). Zo zadania vyplýva, že štvoruholníky \(ADPI\), \(EBFP\) a \(HPGC\) sú rovnobežníky, preto \(|IP| = |AD|=3x\) a \(|PF|=|EB|=2x\). Potom \(|AB|=|AD|+|DE|+|EB|=3x+4x+2x=9x\).

Keďže trojuholníky \(ABC\) a \(DEP\) sú podobné a \(|AB|:|DE|=9:4\), z vyššie odvodeného vzťahu vyplýva: \[S:S_3= 9^2:4^2= 81:16.\] Príklad je teraz už takmer vyriešený, stačí nám z predchádzajúcej rovnice vyjadriť obsah celého trojuholníka: \[S=\frac{81}{16} S_3=\frac{81}{16}\cdot 16=81.\] Obsah celej trojuholníkovej podlahy \(ABC\) je \(81\, \text{cm}^2\).