9. Krásy Malebného Slovenska vzorové riešenie

Najprv spravme zopár dôležitých pozorovaní, ktoré budeme môcť využiť a vďaka ktorým nebudeme musieť skúšať blbosti.

• Nerovnosti sú homogénne – t.j. môžeme všetky premenné predeliť alebo vynásobiť ľubovoľným kladným číslom (pre všetky tri rovnakým) a nezmení to hodnotu výrazu. Tento poznatok je dôležitý vďaka tomu, že nám to umožňuje spraviť predpoklad \(a+b+c=1\) alebo \(abc=1\).

• Nerovnosti sú symetrické. To znamená, že pre ľubovoľnú trojicu \(a\), \(b\), \(c\) nadobúda výraz v strede rovnakú hodnotu pre všetky jej permutácie. Vďaka tomu môžeme urobiť predpoklad \(a \ge b \ge c\).

• Po vyskúšaní pár hodnôt (trebárs keď s \(c\) ideme k nule a \(a\) a \(b\) sa nám v dôsledku trojuholníkovej nerovnosti takmer rovnajú) zisťujeme, že ľavá nerovnosť je naším výrazom „limitne“ (t.j. ľubovoľne tesne) dosiahnuteľná. Naopak, o pravej nerovnosti sa to povedať nedá – po vyskúšaní mnohých dosadení \(a\), \(b\), \(c\) sú hodnoty výrazu od \(\sqrt{6}\) nezanedbateľne ďaleko. Čo z toho vyplýva? Že pri tej ľavej strane musíme byť opatrnejší pri odhadoch – čím bližšie je hodnota nášho výrazu k \(2\), tým tesnejší náš odhad musí byť. Naopak, pri pravej nerovnosti si môžeme dovoliť aj odhady, ktoré nezanedbateľne zväčšujú hodnotu výrazu pre ľubovoľné dosadenie – ak nebudú príliš hrubé, máme stále záruku ostrej nerovnosti.

• Zároveň sa dá všimnúť, že tá ľavá nerovnosť platí bez ohľadu na to, či máme strany trojuholníka alebo nie, zatiaľ čo tá pravá je od tohto predpokladu závislá – voľbou obrovského \(a\) a malých \(b\), \(c\) by náš výraz \(\sqrt{a/(b+c)}\) presiahol ľubovoľnú konštantu. Z toho vyplýva, že pri dokazovaní pravej nerovnosti tento predpoklad určite využijeme (avšak pomôcť nám, samozrejme, môže aj pri dokazovaní ľavej, keďže ju musíme dokázať pre výrazne menšie množstvo hodnôt \(a\), \(b\), \(c\)).

Dosť bolo filozofovania, pozrime sa na pravú nerovnosť. Chceme teda dokázať, že pre všetky \(a\), \(b\), \(c\), ktoré tvoria strany trojuholníka platí: \[\sqrt{\frac{\vphantom{b}a}{b+c}}+\sqrt{\frac{b}{a+c}}+\sqrt{\frac{\vphantom{b}c}{a+b}} < \sqrt{6}.\] Predpokladajme, že \(a \ge b \ge c\). Vidíme tu súčet troch odmocnín na strane menšieho výrazu a aj na pravej strane vidíme odmocninu. Čo nám napadne? No predsa Cauchyho-Schwarzova nerovnosť v odmocninovom tvare¹. Pripomeňme si ju:

\[\sqrt{a_1b_1}+\sqrt{a_2b_2}+ \dots + \sqrt{a_nb_n} < \sqrt{(a_1+a_2+\dots +a_n)(b_1+b_2+\dots +b_n)}\]

Toto platí pre všetky \(a, b, c\) nezáporné. To, že je to dôsledkom klasického tvaru Cauchyho-Schwarzovej (CS) nerovnosti, si môžete dokázať.

Jej priamym využitím by úloha vyriešiť išla, ukážeme si však riešenie, vďaka ktorému po použití CS nerovnosti nebudeme musieť robiť žiadne ďalšie odhady či úpravy. Potrebujeme nejako zjednodušiť výraz na ľavej strane. Všimnime si, že za \(b\)-čka v našej CS nerovnosti budeme musieť zvoliť zlomky. Pri zlomkoch s rôznymi menovateľmi by nám v čitateľoch vznikali veci, ktoré by sa nedali dobre „škrtať“, resp. celkovo by sa nám s nimi zle pracovalo, lebo by to boli rôzne zmiešaniny písmen druhého stupňa. To nás môže naviesť na myšlienku, že chceme ešte pred použitím CS nerovnosti poodhadovať náš výraz tak, aby sme mali rovnaké menovatele. Po tejto myšlienke už nemáme veľa roboty – potrebujeme menovatele zmenšiť (aby sme zväčšili náš výraz, čo je pri tejto nerovnosti smer odhadovania). Teda takmer jediná rozumná myšlienka je nahradiť \(a\) v menovateľoch \(\sqrt{b/(a+c)}\) a \(\sqrt{c/(a+b)}\) \(b\)-čkom a \(c\)-čkom (v danom poradí). Dostávame takýto výraz: \[\sqrt{\frac{\vphantom{b}a}{b+c}}+\sqrt{\frac{b}{b+c}}+\sqrt{\frac{\vphantom{b}c}{b+c}}.\]

Nie je ťažké uhádnuť, že to \(a\) v prvom sčítanci bude teraz problematické, keďže je momentálne vo výraze samo. Ako sa ho zbaviť? Tentoraz je v čitateli, teda ho potrebujeme nahradiť väčším výrazom. Tu sa priam na zlatom podnose núka možnosť využiť trojuholníkovú nerovnosť \(a<b+c\). Nielenže sa zbavíme \(a\)-čka, navyše aj konečne spravíme ostrý odhad, ktorý k našej nerovnosti potrebujeme. Keď to spravíme, dostávame \[\sqrt{\frac{\vphantom{b}a}{b+c}}+\sqrt{\frac{\vphantom{b}b}{a+c}}+\sqrt{\frac{\vphantom{b}c}{a+b}} \le \sqrt{\frac{\vphantom{b}a}{b+c}}+\sqrt{\frac{\vphantom{b}b}{b+c}}+\sqrt{\frac{\vphantom{b}c}{b+c}} < \sqrt{\frac{\vphantom{b}b+c}{b+c}}+\sqrt{\vphantom{b}\frac{b}{b+c}}+\sqrt{\frac{\vphantom{b}c}{b+c}}.\] To už je podstatne krajšie, a v tomto momente vám odporúčam prestať čítať túto polovicu vzoráku a skúsiť úlohu dopočítať.

Pre tých lenivších to spravím ja. Na tento výraz už stačí iba priamo aplikovať CS nerovnosť v odmocninovom tvare. Voľbou \(a\)-čiek čitateľov a \(b\)-čiek menovateľov (áno, dochádza tu k písmenkovej duplicite) dostávame:

\[\sqrt{\frac{b+c}{b+c}}+\sqrt{\frac{b}{b+c}}+\sqrt{\frac{\vphantom{b}c}{b+c}} \le \sqrt{(b+c+b+c)(\frac{3\vphantom{b}}{b+c})} = \sqrt{6},\] čo je presne to, čo sme chceli dokázať.

Pozrime sa teraz na druhú našu nerovnosť. Chceme ukázať: \[2 < \sqrt{\frac{a\vphantom{b}}{b+c}}+\sqrt{\frac{b\vphantom{b}}{a+c}}+\sqrt{\frac{c\vphantom{b}}{a+b}}.\] Spravme pre zmenu predpoklad \(a+b+c=1\). Na zjavné zjednodušenie výrazu by nám teraz pomohlo, keby sme súčty v menovateľoch postupne nahradili výrazmi \(1-a\), \(1-b\), \(1-c\). Vidíme tu tri rovnaké funkcie s inými argumentami. Pri takomto čomsi by nám mohla napadnúť Jensenová nerovnosť. Žiaľ, skúsil som a nič dobré mi nevyšlo.

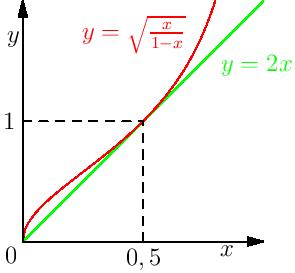
Okrem toho by sme sa ale mohli pokúsiť odhadnúť tieto výrazy samostatne. Nahradiť ich nejakou vhodnou, menšou funkciou. Čo od takejto funkcie očakávame? V provom rade, všetky tri písmenká teraz patria do intervalu \((0;0,5)\), pretože ich súčet je 1 a zároveň stále platí trojuholníková nerovnosť (tak predsa sme ju využili, hoci po dočítaní sa môžete zamyslieť, že sme ju v skutočnosti využiť nemuseli), teda žiadne číslo nemôže byť väčšie rovné \(0,5\). Zároveň, pri hodnotách blízkych nule by mala mať naša funkcia tiež hodnoty blízke nule, pretože iba tak môže byť menšia rovná ako naša \(\sqrt{a/(1-a)}\). Takisto pri hodnotách blízkych \(0,5\) by naša funkcia mala mať hodnoty blízke \(1\), pretože náš výraz je v \(0,5\) rovný jednej a už sme si povedali, že pri týchto hodnotách dosahuje náš celkový výraz hodnoty nebezpečne blízke \(2\), teda náš odhad musí byť pri týchto hodnotách veľmi tesný.

Vhodnou funkciou spĺňajúcou tieto nesmierne náročné požiadavky sa ukazuje byť funkcia \(f(a)=2a\). Tá je v nule rovná nule a v polovici je rovná jednej, navyše pre všetky \(a\) patriace do intervalu \((0;0,5)\) platí: \(\sqrt{a/(1-a)} > 2a\). Toto tvrdenie si môžeme potvrdiť (v zmysle vnútorne sa o ňom presvedčiť) obrázkom. Dokázať ho môžeme veľmi jednoduchými úpravami (skúste si, je to naozaj prístupné). Po urobení tohto odhadu pre všetky tri sčítance nášho výrazu dostávame \[\sqrt{\frac{\vphantom{b}a}{1-a}}+\sqrt{\frac{\vphantom{b}b}{1-b}}+\sqrt{\frac{\vphantom{b}c}{1-c}} > 2a+2b+2c=2\] vďaka nášmu predpokladu \(a+b+c=1\).

Komentár k riešeniam

Musím vás pochváliť sa neuveriteľnú vynaliezavosť. Až pri čítaní vašich riešení som zistil, že mnohé cesty, ktoré som považoval za slepé, naozaj viedli k cieľu. Zároveň chcem pochváliť vaše vedomosti nerovností, keďže niektorí z vás využívali ozaj exotické alebo vysokoškolské nerovnosti.