Zadanie
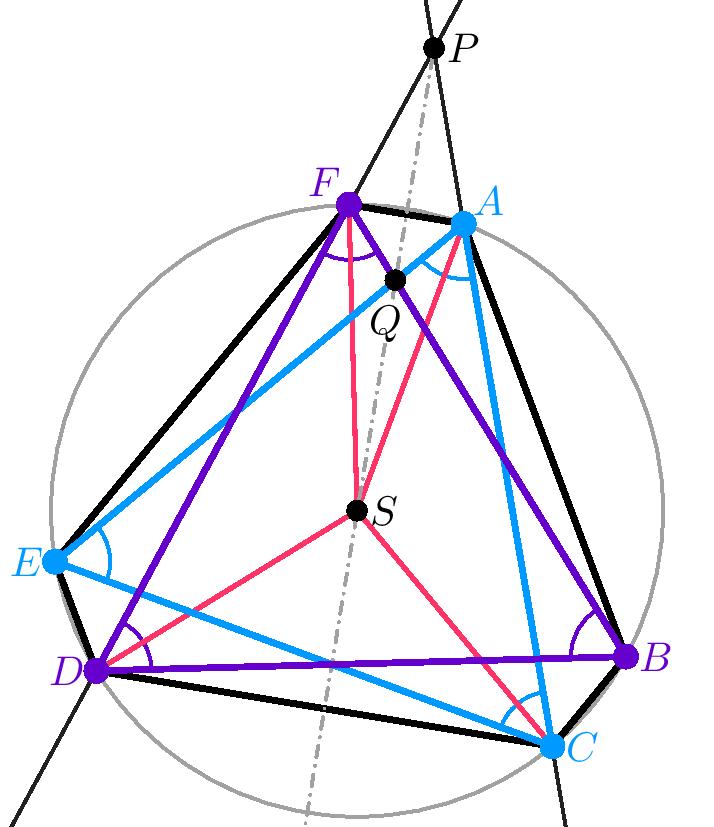
Jurkovi nechutilo soté, čo mal na obed, tak namiesto jedenia obdivoval svoju tácku. Tácka má tvar šesťuholníka \(ABCDEF\) a je položená na kruhovom obruse tak, že všetky vrcholy šesťuholníka \(ABCDEF\) ležia na jeho obvode. Jurko si začal po tácke a po stole kresliť a označil si priesečník priamok \(AC\) a \(FD\) ako \(P\) a priesečník priamok \(AE\) a \(BF\) ako \(Q\). Potom si všimol, že platí \(|BF|=|BD|\), \(|AC|=|CE|\), \(|PA|=|PF|\) a že priamka \(PQ\) je osou uhla \(APF\). Zistite pomer obsahov trojuholníkov \(ACE\) a \(BDF\).
Naším prvým krokom bude spísanie si všetkých daných vecí:
- body \(A\), \(B\), \(C\), \(D\), \(E\), \(F\) ležia na kružnici;
- bod \(P\) je priesečníkom priamok \(AC\) a \(DF\), pričom \(|AP|=|FP|\);
- bod \(Q\) je priesečníkom priamok \(AE\) a \(BF\);
- priamka \(PQ\) je osou uhla \(APF\);
- \(|BF|=|BD|\);
- \(|AC|=|CE|\).
Našou úlohou je zistiť pomer obsahov trojuholníkov \(ACE\) a \(BDF\). Poďme teda na to.
Už pri prvom (dobrom) náčrte si môžeme všimnúť, že ide o symetrickú úlohu. Úsečky \(AP\) a \(FP\) sú rovnako dlhé, takže trojuholník \(APF\) je rovnoramenný. Zjavne os základne rovnoramenného trojuholníka prechádza vrcholom oproti nej a je zhodná s osou uhla medzi ramenami. Keď tento fakt aplikujeme na našu úlohu, zistíme, že body \(P\) a \(Q\) ležia na osi úsečky \(AF\). To znamená, že táto os je totožná s priamkou \(PQ\). O nej zas vieme, že je osou uhla \(APF\). Ľubovoľný bod na osi úsečky je rovnako vzdialený od jej krajných bodov. Ak teda \(Q\) leží na osi úsečky \(AF\), musí platiť, že \(|AQ|=|FQ|\).
Teraz presuňme našu pozornosť na uhly. Zo zadania vieme, že trojuholníky \(BDF\) a \(ACE\) sú tiež rovnoramenné. Preto uhly pri ich základniach sú rovnaké, teda \(|∢EAC|=|∢CEA|\) a \(|∢DFB|=|CDF|\).
Vieme, že \(|∢PFA|=|∢PAF|\) a taktiež \(|∢AFQ|=|∢FAQ|\) (pretože \(|AQ|=|FQ|\)). Potom uhol \(DFQ\), resp. \(DFB\) vieme vyjadriť ako \(180\si{\degree}-|∢PFA|-|∢AFQ|\). Podobne vieme uhol \(CAQ\), resp. \(CAE\) vyjadriť ako \(180\si{\degree}-|∢PAF|-|∢FAQ|\). Z toho vidíme, že uhly \(DFB\) a \(CAE\) sú rovnaké.
Trojuholníky, ktoré máme porovnávať majú teda rovnaké vnútorné uhly – sú podobné. Pozor! To však ešte neznamená, že sú zhodné. Aby sme mohli povedať, že majú rovnako dlhé strany potrebujeme kružnicu. Každému trojuholníku vieme jednoznačne opísať kružnicu. Pre trojuholníky \(ACE\) a \(BDF\) je to tá istá kružnica. Označme si \(S\) jej stred. Bod \(S\) leží na osi strany \(AF\) (úsečke \(PQ\)), pretože je rovnako vzdialený od oboch týchto bodov. Keď bod \(S\) spojíme s ľubovoľnými dvoma bodmi z množiny \(\{A,B,C,D,E,F\}\), tak vytvoríme rovnoramenný trojuholník, nakoľko bod \(S\) je rovnako vzdialený od všetkých. Na základe toho vieme jednoducho dokázať, že aj \(|∢FBD|=|∢ACE|=|∢BDF|=|∢CEA|=|∢DFB|=|∢EAC|\). Teda trojuholníky \(ACE\) a \(BDF\) sú rovnostranné. Majú tú istú opísanú kružnicu, z čoho vyplýva, že sú zhodné. Ak nevidíte prečo, tak si porátame dĺžku strany, ktorú si označíme \(a\). Konkrétne ju vyjadríme pomocou polomeru kružnice.
V rovnostrannom trojuholníku je stred opísanej kružnice aj ťažiskom. Ťažnice sú súčasne výškami. Polomer tvorí \(\frac{2}{3}\) výšky. Teda \(\frac{3}{2}r=v\). Výšku vieme vypočítať z Pytagorovej vety. Tá nám v tomto prípade tvrdí \(a^2=v^2+(a/2)^2\), z čoho keď vyjadríme \(a\) dostávame: \[a=\dfrac{2}{\sqrt3}v=\sqrt3 r.\] Polomer je v oboch trojuholníkoch rovnaký, pretože majú tú istú opísanú kružnicu. Potom majú teda aj rovnaké strany. Tým je dokázané, že trojuholníky \(ACE\) a \(BDF\) sú zhodné a teda: \[ \dfrac{S_{ACE}}{S_{BDF}}=1. \] Taktiež si môžete premyslieť, že trojuholník \(BDF\) je vlastne otočením trojuholníka \(ACE\) alebo naopak.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.