9. Kuchárky Montujú Svetlá vzorové riešenie

Toto je jedna z úloh, kde prísť na správny výsledok je jednoduché. Stačí si nakresliť zopár jedální a pohrať sa s lampami. Podstatne zložitejšie je ukázať, prečo menej lámp nestačí. Preto rovno na začiatok odbavíme tú ľahšiu časť. Uvedieme najmenší počet lámp potrebný na osvetlenie jedálne a ukážeme, akým rozmiestnením lámp ho môžeme dosiahnuť.

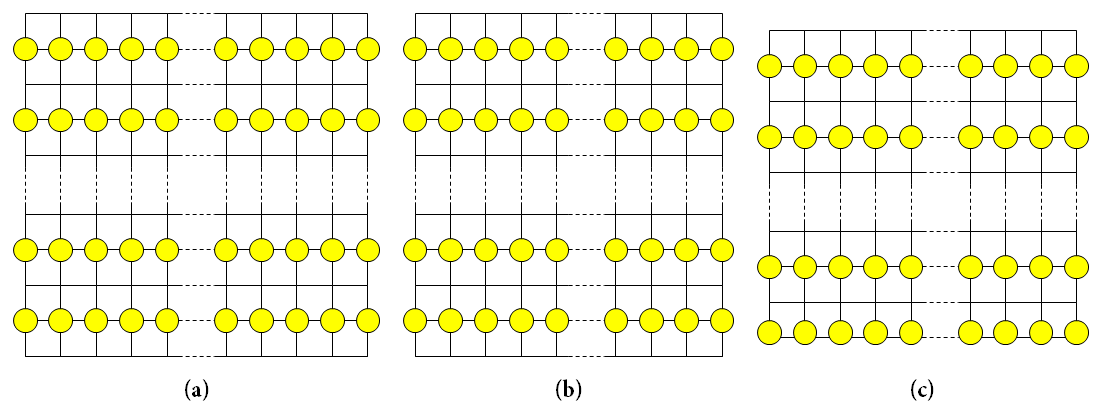
• Ak sú \(m\), \(n\) párne, pričom \(m \le n\), tak nám stačí \(m(n + 1)/2\) lámp. Lamy umiestnime ako na obrázku a.
• Ak je \(m\) párne a \(n\) nepárne, tak nám stačí \(m(n+1)/2\) lámp. Umiestnime ich ako na obrázku b.
• Ak sú \(m\), \(n\) nepárne, tak nám stačí \((m+1)(n+1)/2\) lámp. Umiestnime ich ako na obrázku c.

Teraz sa môžeme pustiť do dokazovania, prečo sú toto najmenšie počty lámp. Budeme sa snažiť ukázať, že na osvetlenie jedálne potrebujeme aspoň \(x\) lámp, t. j. hľadať dolný odhad počtu lámp. Keď sa s dolným odhadom dostaneme k spomenutým počtom lámp, ukážeme, že spomenuté počty sú najmenšie možné. Pre lepšie vyjadrovanie si očíslujeme riadky číslami \(1\) až \(m\) a stĺpce číslami \(1\) až \(n\). Políčko, ktoré sa nachádza v \(r\)-tom riadku a \(s\)-tom stĺpci, budeme označovať ako políčko \((r, s)\). Rozmyslite si, ako by ste opísali vyššie spomenuté rozmiestnenia lámp pomocou týchto označení, bez použitia obrázkov.

Ak sa pozrieme na jedno políčko, tak aby sme ho osvetlili, potrebujeme aspoň dve lampy. Koľko lámp potrebujeme na osvetlenie dvoch políčok? Ak majú spoločnú stranu, tak stále to sú dve lampy. Ak si však zoberieme dve políčka, ktoré nemajú žiaden spoločný vrchol, tak na ne potrebujeme až štyri lampy. Tu vidíme, že pomocou takýchto nesusedných políčok vieme získať celkom pekné dolné odhady. Koľko najviac takých políčok vieme v jedálni \(m \times n\) políčok nájsť?

Zoberme si políčka, ktoré sa nachádzajú v nepárnom riadku a zároveň nepárnom stĺpci (pozri obrázok). Takýchto políčok je \(\lceil m/2 \rceil \lceil n/2 \rceil\).¹ Každá lampa osvetlí najviac jedno z vybraných políčok. Preto na osvetlenie vybraných políčok potrebujeme aspoň \(2\lceil m/2 \rceil \lceil n/2 \rceil\). Ak sa pozrieme na naše výsledky, tak v prípade, keď aspoň jedno z čísel \(m\), \(n\) je nepárne, tak tento počet lámp vieme dosiahnuť. Ostáva nám teda prípad, kedy sú \(m\) aj \(n\) párne.

Užitočným spôsobom dokazovania (a teda aj dokazovania dolných odhadov) je matematická indukcia. Jej princípom je, že jedáleň zmenšíme a z indukčného predpokladu budeme vedieť minimálny počet lámp potrebný na osvetlenie menšej časti. Kľúčovou vecou je určiť, ako máme jedáleň zmenšiť. Totiž priamočiare nápady, ako napr. odstrániť jeden či dva rady stolov, nefungujú. Potrebujeme vymyslieť rafinovanejší spôsob. Tým bude, že odrežeme dva riadky aj dva stĺpce.

Čo však s tým, že máme dve premenné? V matematickej indukcii môžeme využívať len jednu. S tým sa dá popasovať rôznymi spôsobmi. Prvou možnosťou je robiť indukciu podľa jednej premennej, napr. \(m\), a na druhú premennú \(n\) sa dívať ako na parameter, ktorý môže nadobúdať ľubovoľnú hodnotu. Druhou možnosťou, je použiť novú premennú, do ktorej tieto dve premenné \(m\), \(n\) zabalíme. Štandardný spôsob je robiť indukciu podľa \(s = m + n\). Okrem toho sa dá vymyslieť ešte plno ďalších nápadov. Podstatou je nejako si zoradiť jedálne podľa veľkosti a výsledok pre väčšiu jedáleň odvodiť z výsledkov pre menšie jedálne. My použijeme prvý spôsob. Poďme teda našu indukciu riadne zapísať.

Dokážeme, že na osvetlenie jedálne rozmerov \(m \times n\), kde \(m\), \(n\) sú ľubovoľné nezáporné párne čísla také, že \(m \le n\), potrebujeme aspoň \(m(n+1)/2\) lámp. To ukážeme matematickou indukciou podľa \(m\).

Ak \(m = 0\) a \(n\) je ľubovoľné nezáporné celé číslo, tak potrebujeme aspoň \(0\) lámp, teda pre \(m = 0\) dokazované tvrdenie platí.

Predpokladajme, že pre \(m = k\), kde \(k\) je nezáporné párne číslo, a ľubovoľné nezáporné celé párne číslo \(l\) potrebujeme na osvetlenie jedálne rozmerov \(k \times l\) aspoň \(k(l+1)/2\) lámp. Uvažujme teraz jedáleň rozmerov \((k+2) \times n\) (pre ľubovoľné párne \(n\ge k+2\)). Teraz potrebujeme ukázať, že na osvetlenie takejto jedálne potrebujeme aspoň \((k+2)(n+1)/2\) lámp.

V posledom riadku jedálne zafarbíme políčko v každom nepárnom stĺpci a v poslednom stĺpci zafarbíme políčko v každom nepárnom riadku (pozri obrázok). Takto sme zafarbili \((k + 2)/2 + n/2\) políčok. Iba jedna lampa osvetlí dve zafarbené políčka, a to lampa na spoločnom rohu políčok \((k + 2, n - 1)\) a \((k+1,n)\). Okrem nej každá lampa osvetlí najviac jedno zafarbené políčko. Preto na osvetlenie zafarbených políčok potrebujeme aspoň \(2((k + 2)/2 + n/2) - 1 = k + n + 1\) lámp.

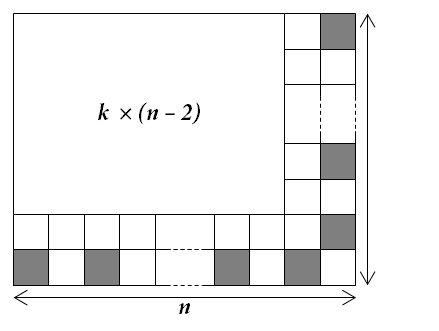
Zoberme si časť jedálne tvorenú celou jedálňou bez posledných dvoch riadkov a bez posledných dvoch stĺpcov. Ide teda o časť jedálne rozmerov \(k \times (n - 2)\). Preto podľa nášho indukčného predpokladu na osvetlenie tejto časti potrebujeme aspoň \(k(n - 2 + 1)/2\) lámp. Položili sme pritom \(l = n - 2\), čo je vďaka tomu, že \(n \ge m = k + 2 \ge 2\) naozaj nezáporné celé párne číslo. Žiadna z týchto lámp neosvetlí zafarbené políčko. Preto na osvetlenie celej jedálne \((k + 2) \times n\) potrebujeme aspoň \[\frac{k(n - 1)}{2} + \frac{2k + 2n}{2} = \frac{kn - k + 2k + 2n}{2} + 1 = \frac{k(n + 1) + 2(n + 1)}{2} = \frac{(k+2)(n+1)}{2}\] lámp. To je presne to, čo sme chceli ukázať. Náš dôkaz matematickou indukciou je hotový. Teda na osvetlenie jedálne párnych rozmerov \(m \times n\) potrebujeme aspoň \(m(n+1)/2\) lámp. Tým sme dokázali všetky potrebné dolné odhady.

Na záver tohto riešenia ešte poukážeme na pre niekoho neštandardný spôsob prvého kroku indukcie. Človek by typicky čakal za prvý krok zobrať jedáleň rozmerov \(2 \times n\). To, samozrejme, kľudne môžeme spraviť a následne nahradiť všade nezáporné čísla kladnými. Avšak matematici sú lenivé tvory a robili by tým prácu navyše. Ukázať dokazované tvrdenie pre \(m = 2\) sa dá tak isto, ako opisujeme dôkaz pre jedáleň \((k + 2) \times n\). Preto nie je potrebné to písať dvakrát a vieme to takto elegantne obísť. Ak však máte problémy sa s tým zmieriť, odporúčame vám vo svojich riešeniach neexperimentovať a radšej za prvý krok zobrať \(m = 2\).