Zadanie
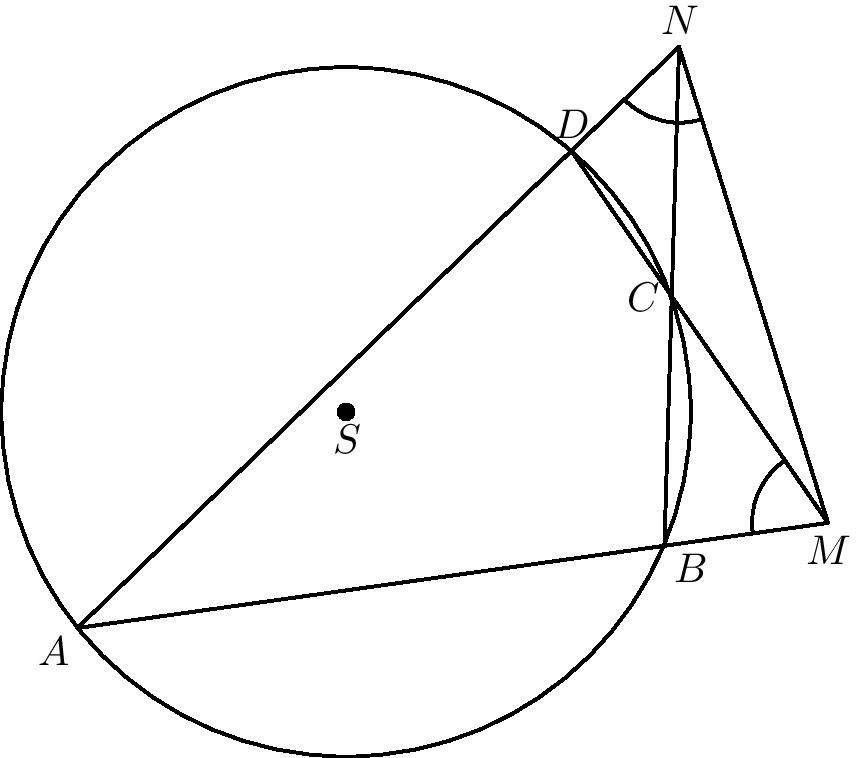
Ku správnej štedrej večeri patrí adventný veniec. Najlepšie taký, ktorý má tvar kružnice \(k\), na ktorej ležia sviečky v štyroch rôznych bodoch \(A\), \(B\), \(C\), \(D\) v tomto poradí. Ďalej polpriamky \(AB\) a \(DC\) sa pretínajú v bode \(M\) a polpriamky \(BC\) a \(AD\) sa pretínajú v bode \(N\). Navyše platí, že \(|\sphericalangle BMC|=|\sphericalangle ANM|\) a \(|BC|=|CN|\). Prečo je takýto veniec najlepší? Lebo body \(M\), \(N\) sú rovnako vzdialené od stredu kružnice \(k\). Dokážte to!
Hlavná myšlienka, ktorá sa používa pri zisťovaní vzdialenosti bodu od kružnice je mocnosť. Ak majú dva body rovnakú mocnosť ku kružnici, tak sú rovnako vzdialené od jej stredu1. Preto budeme dokazovať, že \(|NB| \cdot |NC| = |MA| \cdot |MB|\).
Prvé zistenie je, že trojuholník \(BMN\) je rovnostranný so základňou \(BM\). Toto sa dalo dokázať napríklad obyčajným vyuhlením, cez podobnosti trojuholníkov a mnoho inými metódami.
Najjednoduchšia sa nám zdala táto: trojuholníky \(ADM\) a \(AMN\) majú zo zadania rovnaký jeden uhol a pri vrchole \(A\) majú druhý rovnaký, preto sú podobné. Potom ale \(|\sphericalangle NMA|=| \sphericalangle ADM|\) Vidíme, že štvoruholník \(ABCD\) je tetivový, preto majú protiľahlé uhly súčet \(180^\circ\) , a teda \(|\sphericalangle ADC|=|\sphericalangle MBC|\). Získavame tak \(|\sphericalangle NMA|=|\sphericalangle ADM|=|\sphericalangle ADC|=|\sphericalangle MBC|\). Teda trojuholník \(BMN\) je rovnoramenný.
Trojuholníky \(AMN\) a \(CBM\) sú podobné, keďže \(|\sphericalangle AMN| = |\sphericalangle CBM|\) z rovnoramennosti, a \(|\sphericalangle ANM| = |\sphericalangle CMB|\). Už to skoro ale máme, stačí využiť ich pomery. Platí teda \(|CB|/|MB| = |AM|/|NM|\) , resp. \(|CB| \cdot |NM|=|AM|\cdot|MB|\).
Použijeme poslednú vec zo zadania, a to rovnosť \(|NC|=|CB|\). Z rovnoramennosti platí aj \(|NB|=|NM|\). Platí teda \(|NC|\cdot|NB| = |CB|\cdot|NM| = |MA|\cdot|MB|\), čo sme chceli dokázať.
Ak neviete čo je mocnosť, určite si o nej prečítajte, napríklad v zbierke KMS na strane 37.↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.