Zadanie
Kúzelník predvádza nasledovné kúzlo. Ukáže publiku štvorčekovú tabuľku \(n\times n\) políčok, ktorej dve políčka v protiľahlých rohoch sú zafarbené načierno a zvyšné políčka sú biele. Kúzelník si vie vyberať buď jeden riadok, alebo jeden stĺpec tabuľky a mávnutím paličky zmeniť farbu všetkým políčkam v ňom. V závislosti od celého čísla \(n \ge 2\) určte, koľko najmenej ďalších políčok (t. j. okrem dvoch protiľahlých rohových, ktoré už sú zafarbené) musí kúzelník pred začiatkom kúzlenia zafarbiť načierno, aby potom mohol svojim kúzlením zafarbiť celú tabuľku nabielo.
Celé riešenie bude spočívať v tom, že nájdeme taký spôsob používania kúziel, aby počet políčok, ktoré sa zmenia, bol minimálny. Teda do zmenených políčok budeme rátať aj tie dve, ktoré sú od začiatku čierne (ktoré musíme potom na konci odpočítať). Samozrejme, musíme tieto dve zafarbené políčka nejako zapojiť do našich úvah, aby sme vylúčili nulu ako minimálny počet zmenených políčok. Ak ukážeme, že najmenší počet políčok, ktoré kúzelník dokáže zmeniť, je \(m\), tak budeme vedieť, že na začiatku potrebuje zafarbiť aspoň \(m - 2\) ďalších políčok načierno. Potom nám už len bude stačiť ukázať, že tabuľka s vhodnými \(m-2\) dofarbenými políčkami ide vybieliť.
Na začiatku si všimnime, že ak použijeme kúzlo na ten istý riadok alebo stĺpec dvakrát, tak to má rovnaký efekt, ako keby sme ho ani nepoužili. Čiže môžeme to zúžiť na situáciu, kedy kúzlo použijeme na každý riadok maximálne raz.
Ak použijeme kúzlo na nejaké políčko dvakrát, tak ostane nezmenené. Z hľadiska počtu zmenených políčok nezáleží, či kúzlo použijeme na štvrtý alebo tretí riadok. Počet bude rovnaký, len ich pozícia bude iná. Čiže záleží akurát iba na počte zmenených riadkov (ktorý budeme označovať \(a\)) a stĺpcov (\(b\)).
Teraz využijeme, že na začiatku máme už dve políčka tabuľky čierne. Bez ujmy na všeobecnosti nech sú to ľavé horné a pravé dolné rohové políčko. Keďže ľavé horné políčko musíme zmeniť, tak vieme povedať, že z dvojice najvyšší riadok a najľavejší stĺpec musí byť použitý pravé jeden. To isté platí aj pre pravý dolný roh, z čoho vyplýva \(2\le a+b \le 2n-2\).
V každom z \(a\) zmenených riadkov \(b\) políčok nezmenilo farbu a \(n-b\) zmenilo farbu. Analogicky to platí aj pre stĺpce. Čiže počet zmenených políčok môžeme vyjadriť pomocou výrazu \(a(n-b)+b(n-a)\). A tento výraz musíme minimalizovať za podmienky \(2\le a+b \le 2n-2\).
Ak si to upravíme do tvaru \(n(a+b)-2ab\), tak môžeme jednoducho pozorovať, čo sa stane s počtom zmenených políčok. Ak \(a\) zväčšíme o jedna, tak počet sa zväčší o \([n(a+1+b)-2(a+1)b] - [n(a+b)-2ab]\), čo sa rovná \(n-2b\) . Podľa tohto úlohu prirodzene rozdelíme na 3 možnosti \(b<n/2\), \(b=n/2\) (len pre párne n), \(b>n/2\). Ak \(b<n/2\), tak zväčšovaním \(a\) sa celkový počet zväčšuje. Ak \(b=n/2\), tak na \(a\) nezáleží, a ak \(b>n/2\), tak sa zväčšením \(a\) sa počet zmenšuje. Z toho vyplýva, že chceme :
| \(b\): | \(b<n/2\) | \(b=n/2\) | \(b>n/2\) |
|---|---|---|---|
| \(a\): | minimálne | nezáleží | maximálne |
A keď opäť použijeme tú istú úvahu pre \(b\), tak dostaneme ďalší riadok tabuľky :
| \(b\): | \(b<n/2\) | \(b=n/2\) | \(b>n/2\) |
|---|---|---|---|
| a: | minimálne | nezáleží | maximálne |
| b: | minimálne | n/2 | maximálne |
Čo presne znamená, že \(a\) a \(b\) majú byť minimálne? Hovorí nám to to, že ak vieme jedno z nich zmenšiť, tak dostaneme menší počet zmenených políčok. Preto sa určite najmenší počet zmenených políčok nacházdza v takých prípadoch, kde \(a\) ani \(b\) nevieme zmenšiť. Podobný význam má aj slovíčko maximálne. Teraz sa pozrime na prípady, ktoré sme dostali:
\(b\) aj \(a\) sú minimálne. Keďže \(2 \le a+b\), tak máme dve možnosti: \(b=2\), \(a=0\) kedy celkový počet prefarbených políčok bude \(2n\) alebo \(b=1\), \(a=1\) celkový počet bude \(2n-2\).
\(b=n/2\) a \(0 \le a \le n\). Počet v tomto prípade bude \(n^2 /2\).
\(b\) aj \(a\) sú maximálne. Keďže \(a+b \le 2n-2\), tak máme opäť dve možnosti: \(b=n\), \(a=n-2\), kedy celkový počet prefarbených bude \(2n\) alebo \(b=n-1\), \(a=n-1\) celkový počet bude \(2n-2\).
Čiže celkovo sme dostali, že môžeme zmeniť minimálne \(2n-2\) políčok. A túto situáciu vieme naozaj dosiahnuť. Napríklad tak, že zafarbíme všetky políčka v prvom riadku a poslednom stĺpci okrem ľavého dolného rohu. A keďže dve políčka už sú zafarbené, tak kúzelník musel ofarbiť ešte minimálne \(2n-4\) políčok.
Iné riešenie
Prísť na spôsob, ako tabuľku vybieliť s dofarbením \(2n - 4\) políčok na čierno je celkom jednoduché. Ukážeme si ešte iný spôsob, ako možno ukázať, že s menším počtom dofarbených políčok to nie je možné. Nebudeme pracovať so žiadnymi výrazmi (veď toto je úloha z kombinatoriky a nie algebry ;)), ale použijeme úvahy, ktoré sa často používajú pri úohách s tabuľkami (a aj inde). Tabuľku sa pokúsime rozdeliť na niekoľko častí tak, aby sme o každej časti vedeli povedať, že v nej musíme ešte zafarbiť aspoň jedno políčko. Potom pre všetky oblasti sčítame naše odhady (musíme si dať pozor na prekrývanie) a dostaneme dolný odhad na počet zafarbených políčok. Naše úvahy budú fungovať len pre \(n \ge 4\). Pre \(n \le 3\) ľahko zvládneme získať sprvány dolný odhad (napr. vyskúšaním všetkých možností).
Políčko v \(r\)-tom riadku a \(s\)-tom stĺpci označíme ako \((r,s)\). Uvažujme nasledovných \(2n - 4\) štvoríc políčok:
- pre každé \(i \in \{2,3,\dots,n-1\}\) štvoricu \((1,1)\), \((i,1)\), \((i,i)\), \((1,i)\) (\(n-2\) štvoríc);
- pre každé \(j \in \{2,3,\dots,n-2\}\) štvoricu \((j+1,j)\), \((n,j)\), \((n,n)\), \((j+1,n)\) (\(n-3\) štvoríc)
- a štvoricu \((2,n-1)\), \((n,n-1)\), \((n,n)\), \((2,n)\).
Rozdelenie políčok do štvoríc pre \(n=7\) ilustruje nasledovný obrázok.
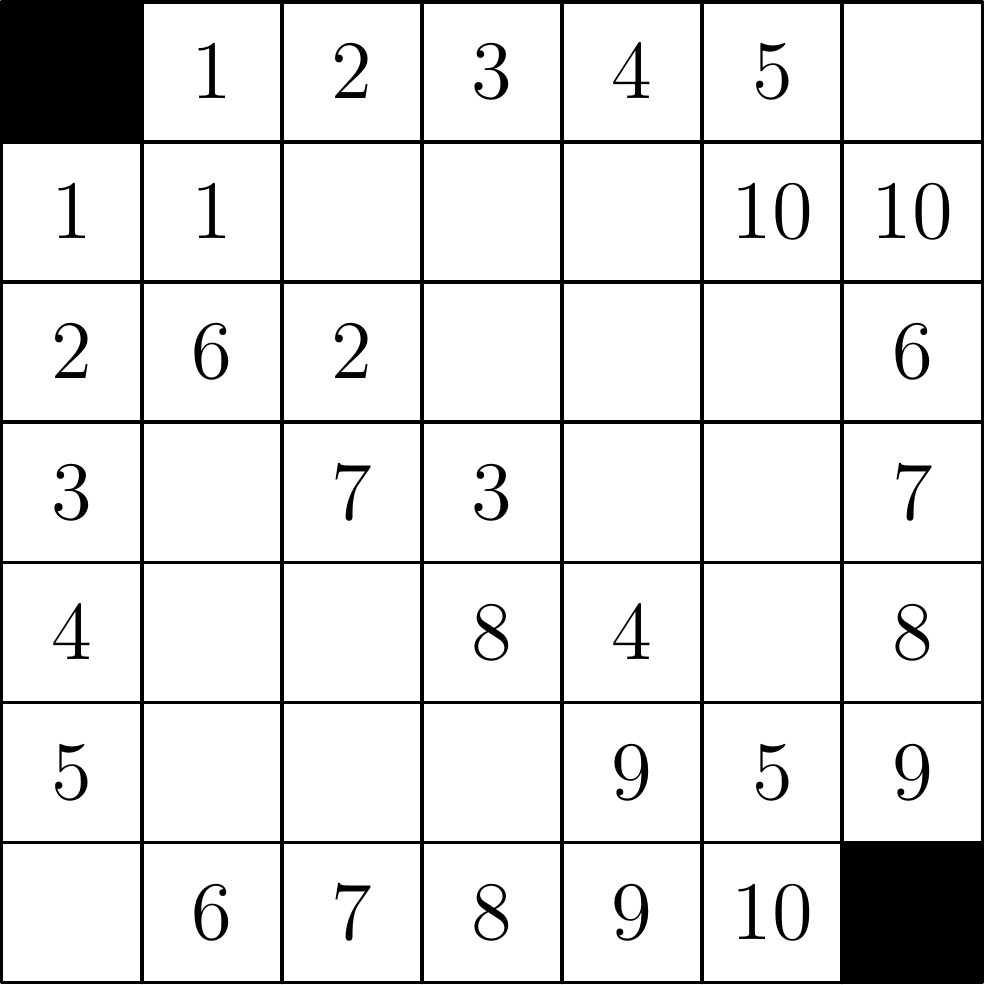
Keďže \(n \ge 4\), okrem políčok \((1,1)\) a \((n,n)\) nemajú tieto štvorice žiadne spoločné políčka. Každá štvorica pozostáva zo štyroch políčok tvoriacich prienik dvoch riadkov a dvoch stĺpcov. Každé mávnutie paličkou mení práve dve políčka z tejto štvorice alebo žiadne. Preto v každej tejto štvorici políčok sa partia počtu čiernych políčok nemení (premyslite si to). Na konci, v bielej tabuľke, má byť v každej štvorici nula čiernych políčok, čo je párny počet. Preto aj na začiatku musí byť v každej štvorici párny počet čiernych políčok. Avšak na začiatku sa v každej štvorici nachádza práve jedno čierne políčko. Teda kúzelník musí v každej štvorici zafarbiť ešte aspoň jedno políčko načierno. Vzhľadom na to, že okrem čiernych políčok \((1,1)\) a \((n,n)\) už štvorice nemajú ďalšie spoločné políčka, potrebuje kúzelník zafarbiť ešte aspoň \(2n-4\) políčok.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.