2. Klábosenie Medzi Spolupasažiermi (κ ≤ 2) vzorové riešenie

Úvod do problematiky

Celkom ťažké na tejto úlohe, obzvlášť pre nových riešiteľov, mohlo byť uvedomiť si, čo nám vlastne hovorí zadanie a čo vlastne máme v tejto úlohe spraviť. Pri ďalšom riešení KMS sa so zložitejšími zadaniami úloh ešte niekoľkokrát stretnete. Preto si ukážeme, ako sa s takýmto zadaním popasovať.

Zadanie nám opisuje nejakú situáciu, konkrétne ako sa pasažieri v lietadle poznajú. Dobrým začiatkom je si situáciu nakresliť. Pasažierov si môžeme zakresliť ako body. Keď sa nejaká dvojica pasažierov pozná, znázorníme to tak, že príslušné body spojíme čiarou.¹ Avšak, ako nám zadanie ďalej opisuje, medzi pasažiermi to nevyzerá len tak hocijako. Kika zistila nejaké vlastnosti toho, ako sa pasažieri poznajú. Prvou vlastnosťou je, že každý sa cez niekoľko známostí pozná s ľubovoľným iným pasažierom. Aby sme sa takto dlho už ďalej nerozpisovali, nazveme si túto vlastnosť tak, že pasažieri sú súvislí. Túto vlastnosť pekne vidno na obrázkoch – sú proste súvislé ;). Ďalšou vlastnosťou je, že nech akokoľvek rozdelíme pasažierov na dve nepráznde skupiny, tak v aspoň jednej skupine bude dvojica, čo sa pozná. Túto vlastnosť budeme nazývať nerozdeliteľnosť. Takže zadanie nám opisuje nejakých pasažierov, ktorí sú súvislí a nerozdeliteľní. Tak poďme si nakresliť niekoľko príkladov takejto situácie.

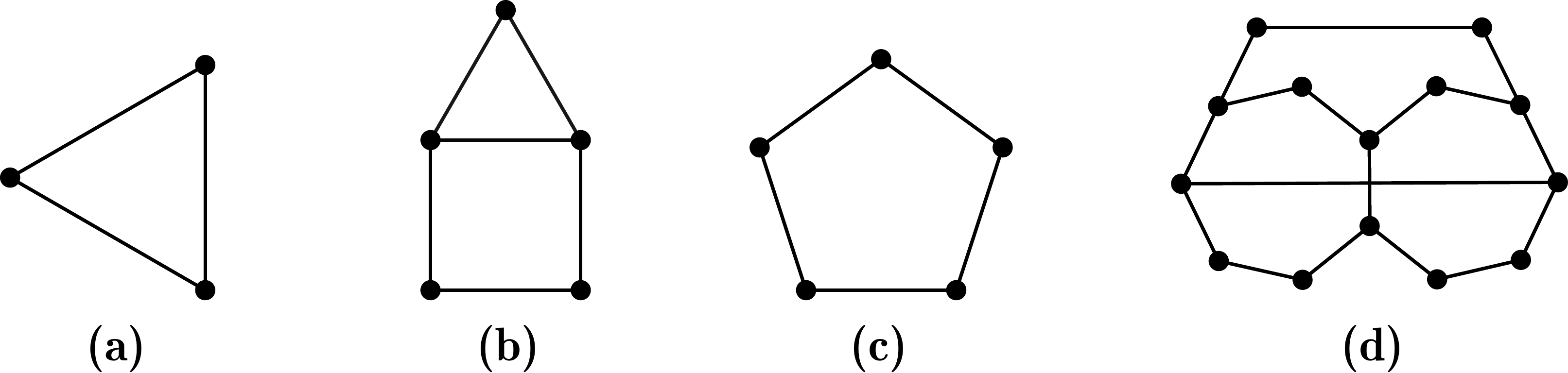
Pri nachádzaní toho, ako sa pasažieri môžu poznať, narazíme na problém s nerozdeliteľnosťou. Nie je to totiž vlastnosť, ktorá by bola vidno z obrázku. Aby sme skontrovali, či naši pasažieri sú skutočne nerozdeliteľní, tak jedna možnosť je vyskúšať všetky možné rozdelenia na dve skupiny a overiť, že v každom rozdelení sa niekto v rámci jednej skupiny pozná. Môže nás ale napadnúť aj iných spôsob, ako nerozdeliteľnosť zaručiť. Napríklad, ak máme trojicu pasažierov, v rámci ktorej sa pozná každý s každým. Také trojice sa nachádzajú na obrázkoch (a) a (b). Taktiež to môžeme dosiahnuť tým, že medzi pasažiermi sa bude nachádzať skupina nepárneho počtu pasažierov, ktorej členovia sa poznajú do kolečka. Obrázok (c) je tvorený práve takouto \(5\)-člennou skupinou. Na obrázku (d) sa nachádzajú viaceré \(7\)-členné a aj \(11\)-členné „kolečko“.

Tým sa dostávame k našej úlohe. Máme totiž ukázať, že existuje skupina aspoň troch ľudí, ktorých možno postaviť do kruhu tak, že každý pozná svojich dvoch susedov. To sú presne tie naše „kolečká“, o ktorých sme nedávno písali. Takéto skupiny ľudí budeme nazývať ako cykly. Našou úlohou teda je ukázať, že medzi pasažiermi existuje cyklus. Môžeme si všimnúť, že situácie, ktoré sme si načrtli, cykly obsahujú. Čo je ale potrebné si uvedomiť, našou úlohou nie je vyriešiť zopár konkrétnych prípadov, ale všetky. Inými slovami, máme ukázať, že ak dostaneme hocikoľko pasažierov, ktorí sa hocijako poznajú tak, že sú súvislí a nerozdeliteľní, tak je medzi nimi cyklus. Možností, ako sa pasažieri môžu poznať je strašne (dokonca nekonečne) veľa a my musíme ukázať, že v každej je cyklus.

Samotné riešenie

Keď sa snažíme nájsť nerozdeliteľných pasažierov, tak to vyzerá tak, že to bez cyklov nejde. Ak si skúsime nakresliť nejakých pasažierov bez cyklu, tak zistíme, že ich možno rozdeliť na dve skupiny, v rámci ktorých sa nikto nebude poznať, teda sa nám pokazí nerozdeliteľnosť. Od týchto našich úvah sa odrazíme a pokúsime sa ich zovšeobecniť. Keď chceme skúšať nájsť pasažierov bez cyklu, tak vlastne skúšame dôkaz sporom. To presne aj spravíme. To znamená, že budeme predpokladať, že máme pasažierov, ktorí sú nerozdeliteľní, súvislí a bez cyklu. A ako naše úvahy naznačili, pokúsime sa dopracovať ku sporu s nerozdeliteľnosťou.

Poďme teda skúsiť pasažierov rozdeliť na dve skupiny. Na začiatok vyberme jedného človeka, nazvime ho Jano a dajme mu číslo \(1\). Všetkých jeho známych očíslujeme číslom \(2\). Všetkých známych dvojok očíslujeme jednotkami, opäť zas všetkých známych jednotiek očíslujeme dvojkami a takto to striedame ďalej, až kým neočíslujeme všetkých.

Teraz máme pasažierov rozdelených na dve skupiny: na tých s číslom \(1\) a tých s číslom \(2\). Čo by sa stalo, ak by sa poznali dvaja ľudia, nazvime si ich \(A\) a \(B\), z tej istej skupiny? Pritom, ako sme pasažierov číslovali, sme sa dostali od Jana k pasažierovi \(A\) po nejakej postupnosti pasažierov a po nejakej inej sme sa dostali k pasažierovi \(B\). V oboch postupnostiach sme používali známosti, v ktorých sa poznali dvaja ľudia z iných skupín. Preto známosť medzi \(A\) a \(B\) sme nemohli použiť. Poďme teraz späť po týchto postupnostiach smerom k Janovi, kým sa nestrenú v nejakom pasažierovi \(C\) (môže to byť aj Jano). Ak by sa \(A\) a \(B\) poznali, tak vieme nájsť cyklus: vyberieme sa od pasažiera \(A\) po známostiach smerom k \(C\), potom od \(C\) k \(B\) a zakončíme to známosťou medzi \(A\) a \(B\). Teda nemôže sa stať, žeby sa dvaja ľudia v rámci jednej skupiny poznali. To ale dostávame spor s tým, že pasažieri sú nerozdeliteľní. Preto musí medzi nimi existovať cyklus.