1. Keď Miluješ Spomienky (κ ≤ 1) vzorové riešenie

Zadanie

Jožovi bolo v Belgicku smutno a tak si pospomínal na časy, keď išiel vedúcovať svoje prvé sústredenie. Organizoval tam hru, ktorá sa hrala v ôsmich miestnostiach. Na začiatku hry sa družinka šiestich účastníkov rozdelila do miestností, každý účastník do inej. Po každom kole sa každý účastník presunie do inej miestnosti. Pritom presúvať sa medzi miestnosťami sa dá len tak, ako je naznačené na obrázku. Dokážte, že bez ohľadu na to, ako sa družinka na začiatku rozdelí, nikdy sa nestretnú všetci jej účastníci v jednej miestnosti.¹

---

1. Bolo by blbé, keby sa takáto hra hrala na sústredení, obzvlášť ak by pre výhru bolo potrebné stretnúť sa jednej miestnosti. Našťastie si vedúci pomáhajú a Viťo pomohol odhaliť Jožovi túto chybičku.↩

Uvedieme dva spôsoby riešenia.

1. spôsob riešenia

V schéme sa nachádza \(8\) miestností a každá je spojená cestou s práve \(3\) ďalšími. Pre lepšiu orientáciu v obrázku si vyfarbime miestnosti dvoma farbami ako je znázornené na obrázku:

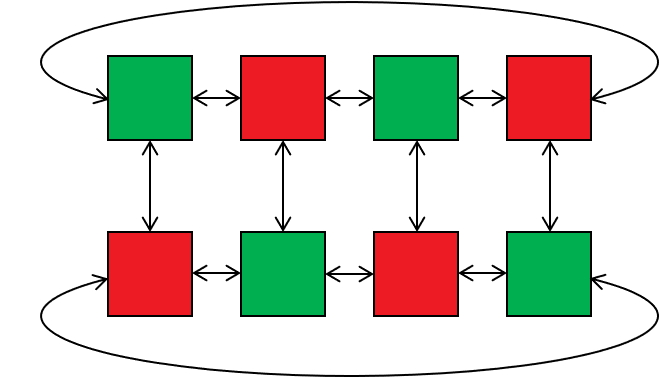
Pre toto ofarbenie platí, že každá miestnosť je cestičkami spojená s práve troma miestnosťami opačnej farby. Máme \(4\) miestnosti zelenej farby a \(4\) miestnosti červenej farby, do nich chceme umiestniť \(6\) účastníkov. Môžeme si všimnúť, že ich na začiatku nevieme všetkých umiestniť do miestností s rovnakou farbou (vždy budú aspoň \(2\) v miestnostiach s opačnou farbou). Po každom kole sa účastníci premiestnia do niektorej z iných miestností, ktoré sú s ich pôvodnou spojené cestičkou. Podľa spôsobu, akým sme miestnosti ofarbovali, vieme, že sa v nasledujúcom kole každý účastník ocitne v miestnosti s opačnou farbou ako v kole predtým. Preto sa v každom kole ocitnú aspoň \(2\) účastníci v miestnosti s opačnou farbou ako zvyšní, a teda vieme zaručiť, že sa ani v jednom kole nestretnú v jednej a tej istej miestnosti všetci \(6\) (keďže sa nestretnú ani len v miestnostiach s rovnakou farbou).

2. spôsob riešenia

Na úlohu sa však môžeme pozrieť aj inak. Máme \(8\) miestností a z každej vedú práve \(3\) cesty. Situáciu teda vieme premeniť na pohyb medzi vrcholmi kocky (pre jednoduchosť nech má dĺžku strán rovnú \(1\)). Vrcholy kocky budú predstavovať dané miestnosti a hrany nám budú určovať cesty medzi miestnosťami. Vrcholy si označíme pomocou súradnicového systému ako je na obrázku:

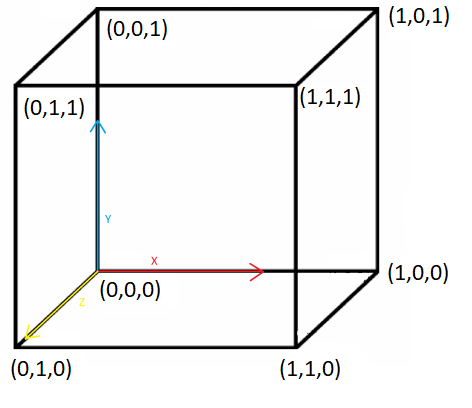
Vďaka tejto reprezentácii si vieme charakterizovať každý vrchol na základe súčtu jeho súradníc. Keď máme situáciu takto prekreslenú, poďme si ju lepšie rozobrať. Z každej miestnosti sa vieme dostať do práve \(3\) ďalších a to pohybom po jednej z osí. Teda pri presune z miestnosti do miestnosti sa vždy zmení práve jedna súradnica z \(0\) na \(1\) alebo naopak. Čiže sa súčtu zmení parita. Toto sa stane pri každom presune každého účastníka. Keď si vrcholy označíme pomocou súčtov, dostávame \(4\) vrcholy s párnym súčtom a \(4\) s nepárnym. Účastníkov máme v úlohe \(6\). To znamená, že ich nemôžeme umiestniť všetkých do vrcholov s rovnakou paritou ale aspoň dvaja budú v miestnostiach s opačnou paritou ako zvyšní. Po každom kroku sa bude parita miestnosti každého účastníka meniť a teda sa nikdy nemôže stať, že budú všetci účastníci naraz v miestnostiach s rovnakou paritou. Z toho dostávame, že sa nemôžu naraz nachádzať ani v rovnakej miestnosti.