Zadanie
Maťko a Vodička sa vydali do lokálneho múzea hornín. Tam našli mramorovú dosku so štvorčekovou sieťou. Maťko s Vodkom sa začali hrať následujúcu hru na štvorčekovom mramore1. Maťko otvorí hru tým, že nakreslí krížik do ľubovoľného štvorčeka. V každom svojom ďalšom ťahu musí nakresliť krížik do voľného štovrčeka, ktorý aspoň vrcholom susedí so štvorčekom, v ktorom je krížik. Vodka môže v jednom ťahu nakresliť tri koliečka do ľubovoľných voľných políčok. Ak Maťko môže nakresliť siedmy krížik, vyhráva. Inak vyhráva Vodička. Zistite, či existuje stratégia pre Vodičku taká, že Maťko zaručene nevie vyhrať.
Keďže ani Maťko ani Vodička nie sú vagabundi, celú hru odohrali v hlavách, na nekonečnej štvorčekovej sieti.↩
Zahráme si pár hier a zistíme, že ak nie je Vodka veľmi hlúpy, tak vie obkľúčiť Maťka tak, aby dal najviac \(6\) \(X\)-iek.
Aká bude Vodkova stratégia? Po Maťkovom prvom \(X\), si nakreslí okolo tohoto \(X\) štvorec veľkosti \(3\times 3\) ako na obrázku (\(X\) je v ňom hore v strede) a nad \(X\) dá svoje tri \(O\). Označíme si políčka, tak ako na obrázku. Vodka teraz dokáže Maťka “zatarasiť” a nechať ho hrať iba v tomto štvorci. Ako? Nech dá Maťko na hociktoré zo zvyšných \(7\) okrajových políčok svoje \(X\), má na dosah iba tri políčka mimo štvorca. Prečo? Pretože jediné dve políčka v celom štvorci, ktoré susedia s viac ako tromi políčkami mimo štvorca, sú dolné rohové políčka \(C_1\) a \(C_3\). S nimi ale musí nejaké \(X\)-ko najprv susediť. To sa môže stať iba cez jedno z políčok \(A_2\), \(S\) a \(B_2\). Ak dá Maťko svoje \(X\) do stredu štvorca \(S\), niekedy v priebehu hry (okrem siedmeho ťahu), tak môže Vodka dať všetky tri svoje \(O\) dovnútra štvorca. Ak nie sú zabraté rohové políčka \(C_1\) a \(C_3\), tak svoje \(O\) dá práve na ne.
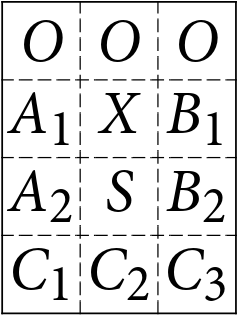
Ostáva teda iba začať na \(A_2\) (\(B_2\)). Ak ale najprv dáme \(X\) na \(A_2\) (\(B_2\)), Vodkova stratégia, bude dať tri \(O\) na tie vonkajšie políčka, s ktorými susedí. Potom, ale rohovému políčku už skutočne ostanú iba tri vonkajšie políčka, s ktorými susedí. Preto nech robí Maťko čokoľvek, Vodka ho vie udržať vo štvorci.
Výborne, už nám stačí dokázať, že Vodka je vždy schopný okrem toho, že Maťka udrží vo štvorci, dostať aspoň tri svoje \(O\) dovnútra štvorca. Ako sme videli vyššie, Maťko nesmie nikdy dať svoje \(X\) (okrem \(7\)meho) do stredu, lebo Vodka potom dá tri \(O\) dovnútra štvorca a vyhral.
Teraz trochu počítania. Za \(6\) kôl, v ktorých musí Vodka úplne zablokovať Maťka, stihne položiť \(18\) svojich \(O\)-čiek. Aby Maťko nemal kam dať siedme \(X\), musia byť \(3\) z toho vo vnútri štvorca. Ostáva nám teda \(15\) \(O\)-čiek, na obkolesenie štvorca. Niečo tu však nesedí. Okolo štvorca je \(16\) políčok a my máme len \(15\) \(O\)-čiek. To však vôbec nevadí, keď si uvedomíme, že jeden z rohov sa nám určite podarí zablokovať priamo, a teda ho už nemusíme blokovať z vonka. Na obkľúčenie nám potom bude stačiť \(15\) \(O\)-čiek a všetko zrazu do seba zapadne.
Teraz už naozaj na záver, ukážeme, že Vodkovi ostane jeden “voľný” ťah pri obkolesovaní skôr, ako sa Maťkovi podarí zablokovať všetky rohy. Na zablokovanie troch rohov potrebuje Maťko aspoň \(4\) ťahy. Jednoduchou analýzou všetkých možností, ktorú prenecháme čitateľovi, však zistíme, že po štvrtom Maťkovom ťahu už Vodka určite nepotrebuje položiť všetky tri \(O\)-čka, lebo niektoré z vonkajších políčok už skôr zablokoval.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.