9. Korporátna Mestská Stabilita vzorové riešenie

Úvod a obsah vzoráku

Na začiatok by sme sa chceli ospravedlniť za to, že zadanie tejto úlohy nebolo dobre sformulované, čo malo za následok, že ste ho pochopili rôzne, väčšina z vás inak, ako sme ho mysleli my. Takže na začiatok si ujasníme zadanie.

Pre lepšiu názornosť nazveme ekonomickou rovnováhou stupňa \(k\), kde \(k\) je kladné celé číslo, stav v krajine, ktorý spĺňa tri podmienky ako sú v odrážkach v zadaní (teda mestá si platia navzájom v hodnotách \(1,\, 2,\, \dots,\, k - 1\) a každé dostáva rovnako veľa ako platí). Chceli sme od vás nájsť pre dané celé číslo \(n \ge 2\) najmenšie také celé číslo \(k\), pre ktoré sa dá v Nemecku s \(2n\) mestami zaviesť ekonomická rovnováha stupňa \(k\) bez ohľadu na to, ako sú jeho mestá pospájané.

To, že máte určiť \(k\) bez ohľadu na pospájanie miest, nebolo v zadní napísané, a tak, celkom pochopiteľne, ste si mnohí mysleli, že sa pýtame na najmenšie \(k\), pre ktoré sa dá pri nejakom pospájaní miest Nemecka zaviesť ekonomická rovnováha stupňa \(k\).

Pre lepšiu názornosť sa pozrieme na prípad, kedy \(n = 3\), teda keď máme \(6\) miest. Mestá budeme znázorňovať ako body a cesty medzi nimi spojnicami. Ak cestu z mesta \(A\) do mesta \(B\) bude vlastniť mesto \(B\), ktorému bude mesto \(A\) platiť denne \(x\) eur, tak to budeme na našich obrázkoch znázorňovať tak, že na spojnicu z mesta \(A\) do mesta \(B\) pridáme v tomto smere šípku a k nej napíšme číslo \(x\). Na obrázku nižšie sú ilustrované dva spôsoby, ako môžu byť mestá poprepájané. V prvom prípade sme našli ekonomickú rovnováhu stupňa \(3\) a pre druhú krajinu stupňa \(4\). Podľa nami mysleného zadania je pre \(n = 3\) hľadané najmenšie \(k = 4\), podľa druhej interpretácie je to \(k = 3\).

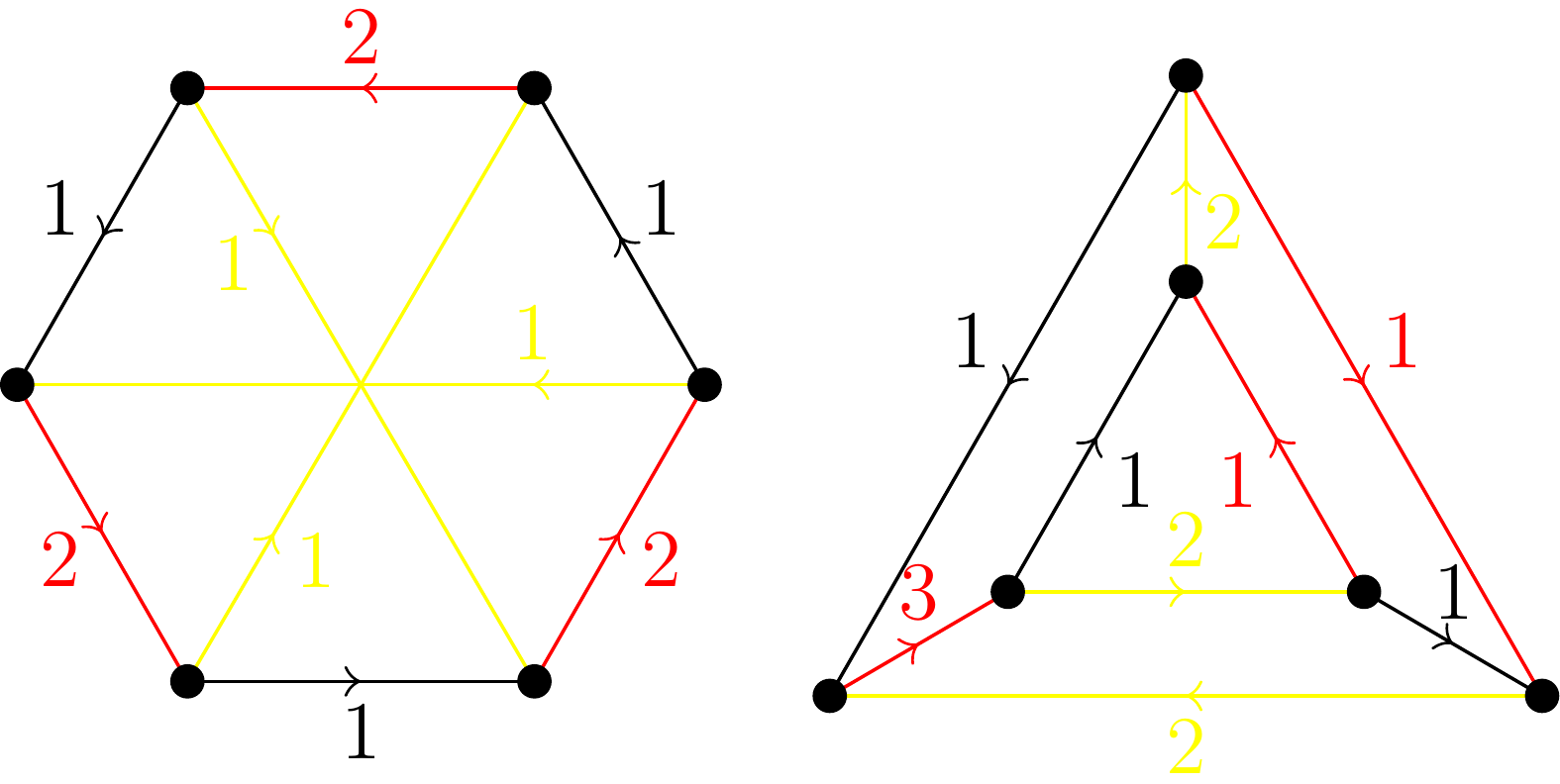
Vzhľadom na túto situáciu si ukážeme riešenie oboch častí. Tento vzorák teda obsahuje:

• Vzorák 1, v ktorom si ukážeme riešenie úlohy, ako sme ju mysleli my.

• Vzorák 2, v ktorom si ukážeme riešenie úlohy, ako ste ju pochopili mnohí z vás.

• Ukážeme si ešte ďalšiu interpretáciu zadania vo vzoráku 3.

• Na záver si povieme ešte niečo o zovšeobecneniach a zaujímavostiach ohľadom tejto úlohy.

Riešenie každej z týchto troch úloh je niečim poučné. Hlavne chceme dať do pozornosti posledný vzorák, nakoľko sa túto interpretáciu úlohy nepodarilo vyriešiť žiadnemu z dvoch riešiteľov.

Vzorák 1

Keď si skúsime úlohu vyriešiť pre malé hodnoty \(n\), isto objavíme situácie, kde je potrebné \(k \ge 4\). Ide napríklad o také poprepájanie miest, v ktorom je trojuholník, teda nejaké tri mestá \(A\), \(B\), \(C\), z ktorých sú každé dve spojené cestou. V takejto krajine musí byť \(k \ge 4\). Ak by išla nastoliť ekonomická rovnováha len s platením \(1\) a \(2\) eur, tak za niektorú cestu medzi mestami \(A\), \(B\), \(C\) by sa museli platiť \(2\) eurá, bez ujmy na všeobecnosti nech mesto \(A\) platí mestu \(B\) \(2\) eurá. Potom \(C\) musí platiť mestu \(A\) \(1\) euro a \(B\) musí platiť mestu \(C\) \(1\) euro. Dostávame tak, že mesto \(C\) dostáva \(1\) euro a platí \(1\) euro, teda tretia cesta túto rovnováhu musí porušiť (rozmyslite si to, celý tento dôkaz je len prebratie niekoľkých prípadov). Pre každé \(n \ge 2\) vieme nájsť krajinu s takýmito tromi navzájom poprepájanými mestami, teda pre každé \(n \ge 2\) určite platí \(k \ge 4\).

Potrebujeme nájsť nejaký systém, ako nájsť pre ľubovoľné poprepájanie \(2n\) miest ekonomickú rovnováhu. Začneme s tým, že máme mestá, ktoré sú ľubovoľne poprepájané cestami. Istá rovnováha je už medzi nimi aj teraz: každé mesto dostáva \(0\) eur a platí tiež \(0\) eur. Akurát sa žiadne peniaze v krajine nehýbu. Ekonomickú rovnováhu budeme hľadať tak, že budeme postupne rozhýbavať peniaze po cestách, pričom budeme zachovávať, aby každé mesto platilo rovnako veľa ako dostáva.

Pri tom nám pekne prídu vhod farebné cesty. Odmyslime si žlté cesty a pozrime sa len na čierne a červené cesty. Z každého mesta teda vychádzajú práve dve cesty. Ak sa z jedného mesta vyberieme po týchto cestách, tak stále máme kam pokračovať – jednou cestou prídeme a druhou odídeme. Raz sa však musíme vrátiť do mesta, v ktorom sme už boli, lebo miest je konečne veľa. Musíme sa vrátiť do mesta, kde sme začali. Totiž, to je jediné mesto, v ktorom sme boli a má ešte nepoužitú cestu. Budeme chodiť teda do kolečka po nejakých mestách. Takéto kolečko budeme nazývať cyklus. Tento červeno-čierny cyklus nemusí prechádzať cez všetky mestá. Ak to tak nie je, tak červeno-čierne cesty vytvárajú viacero cyklov.

Teraz zoberieme tieto červeno-čierne cykly a v každom cykle si mestá budú jedným smerom platiť \(1\) euro. Peniaze nám už začínajú prúdiť, ale stále sú ešte cesty (žlté), za ktoré ešte nikto neplatí. Preto zoberieme podobne červeno-žlté cykly a v každom z nich si budú mestá jedným smerom platiť \(2\) eurá. Peniaze sú už rozprúdené. Za čierne cesty sa platí \(1\) euro a za žlté \(2\) eurá. Pri červených cestách sa mieša platenie jedného a dvoch eur. Ak obe platby idú tomu istému mestu, tak je to rovnaké, ako by to mesto dostávalo \(3\) eurá. Ak mesto \(A\) platí mestu \(B\) \(1\) euro a mesto \(B\) mestu \(A\) \(2\) eurá, tak je to to isté, ako by mesto \(B\) platilo mestu \(A\) \(1\) euro. Teda dostávame, že každá cesta je vlastnená nejakým mestom a že sa za ňu platia \(1\), \(2\) alebo \(3\) eurá. Z toho, ako sme tieto dane určovali, vyplýva, že každé mesto dostáva rovako veľa, ako aj platí. Teda sme našli ekonomickú rovnováhu stupňa \(4\). Keďže sme ukázali, že ekonomická rovnováha nižšieho stupňa ako \(4\) nejde zaviesť vždy, tak hľadané najmenšie \(k\) je rovné \(4\) pre každé celé \(n \ge 2\).

Vzorák 2

V zadaní ešte nebolo úplne jasné, či medzi dvomi mestami môže viesť viac ako jedna cesta. Ako si môžete rozmyslieť, riešenie našej interpretácie úlohy to neovplyvňuje. No pri tejto interpretácii to môže riešenie výrazne zľahčiť. Preto budeme predpokladať, že medzi každými dvoma mestami vedie najviac jedna cesta. Ak máme \(4\) mestá, tak musí cesta viesť medzi každými dvomi mestami. Takéto prepojenie obsahuje trojuholník, a teda pre \(n = 2\) musí byť \(k \ge 4\). Ako sme ukázali v predchádzajúcom riešení, ekonomická rovnováha stupňa \(4\) ide v takejto krajine zavrieť.

Čo sa týka \(n \ge 3\), tak ekonomickú rovnováhu stupňa 2 nemožno zaviesť. Z troch jednoeurových daní totiž nevieme dostať pomocou sčítania a odčítania nulu. Vieme už však nájsť krajiny, v ktorých pôjde zaviesť ekonomická rovnováha stupňa \(3\). Poďme teda opísať, ako vyzerajú. Aby sa nám lepšie opisovali, označíme si mestá v krajine ako \(M_1,\ M_2,\ \dots,\ M_{2n}\). Začneme tým, že si mestá budú do kruhu na striedačku posielať \(1\) a \(2\) eurá. Presnejšie, mesto \(M_{2i}\) bude vlastniť čiernu cestu z mesta \(M_{2i - 1}\), ktoré mu bude platiť denne \(1\) euro. Podobne, mesto \(M_{2i + 1}\) bude vlastniť červenú cestu z mesta \(M_{2i}\), ktoré mu bude platiť \(2\) eurá denne. V oboch prípadoch berieme \(i\) spomedzi čísel \(1,\, 2,\, \dots,\, n\) a \(M_{2n + 1} = M_1\).

Takto má každé mesto s párnym číslom stratu \(1\) euro a každé mesto s nepárnym číslo zisk \(1\) euro. To napravíme tým, že tieto mestá pospájame žltými cestami. Potrebujeme však opísať, ako presne. Pre nepárne \(n\) majú pre každé \(i\in \{1,2,\dots,n\}\) čísla \(i\) a \(n + i\) rôzne parity, preto môžeme spojiť mestá \(M_i\) a \(M_{n + i}\) žltou cestou, za ktorú bude mesto s nepárnym číslom platiť \(1\) euro mestu s párnym číslom. Takto poprepájané mestá spĺňajú všetky podmienky zo zadania (z každého mesta vychádzajú tri cesty rôznych farieb) a zaviedli sme takto na nich ekonomickú rovnováhu stupňa \(3\).

Pre párne \(n\) ide tiež mestá popárovať, no opísať popárovanie je trošičku zložitejšie. Môžeme to napríklad spraviť takto: Pre \(i \in \{2,3,\dots,n - 1\}\) spojíme mesto \(M_{i}\) žltou cestou s mestom \(M_{n - i + 1}\). Okrem toho ešte spojíme žltými cestami mestá \(M_1\) s \(M_{n}\) a \(M_{2n}\) s \(M_{n + 1}\). Čísla miest spojených žltou cestou majú vždy rôznu paritu, tak opäť mesto s nepárnym číslo bude platiť za túto cestu \(1\) euro. Takto sme opäť našli krajinu s ekonomickou rovnováhou stupňa \(3\).

Vzorák 3

Dvaja riešitelia pochopilo úlohu ešte tak, že máme nájsť najmenšie celé \(k\), pre ktoré ide zaviesť ekonomická rovnováha stupňa \(k\) pre každé poprepájanie \(2n\) miest a taktiež aj pre každé rozdelenie toho, komu patria cesty. Musí však platiť, že každé mesto vlastní jednu alebo dve cesty, inak by ekonomická rovnováha triviálne zaviesť nešla. Naznačíme tu stručne jedno z riešení. Budeme predpokladať, že krajina súvislá, teda medzi každými dvoma mestami sa dá prepraviť po niekoľkých cestách.

Ukážeme, že najmenšie je \(k = n + 1\). To je potrebné napr. v krajine ako na obrázku. Cesta, za ktorú sa tam platí \(5\) eur nemôže mať menšiu daň, nakoľko sa jej peniaze na daň piatich ďalších ciest. Zovšeobecnenie pre \(2n\) miest ponechávame na vás.

Teraz ukážeme, že ekonomickú rovnováhu stupňa \(n + 1\) možno vždy zaviesť. Predpokladajme, že tomu tak nie je. Zoberme si krajinu, ktorá to kazí, a nech \(k\) (\(k > n + 1\)) je najmenší stupeň ekonomickej rovnováhy, ktorú možno v nej zaviesť. Potom musí v tejto krajine existovať aspoň \(k - 1\) ciest (teda aspoň \(n + 1\)), ktoré keď odstránime, tak budú existovať dve mestá také, že sa nevieme dostať z jedného do druhého chodením po cestách iba v rovnakom smere, ako po nich idú peniaze. To ale však nie je možné, ak máme len \(2n\) miest. Dôkaz prenecháme vám. To tvrdenie naozaj platí, ale aj napriek tomu je takéto riešenie úlohy nesprávne. Zamyslite sa nad tým prečo. Chyba sa nachádza v samotnej štruktúre dôkazu, nie v nejakých detailoch.

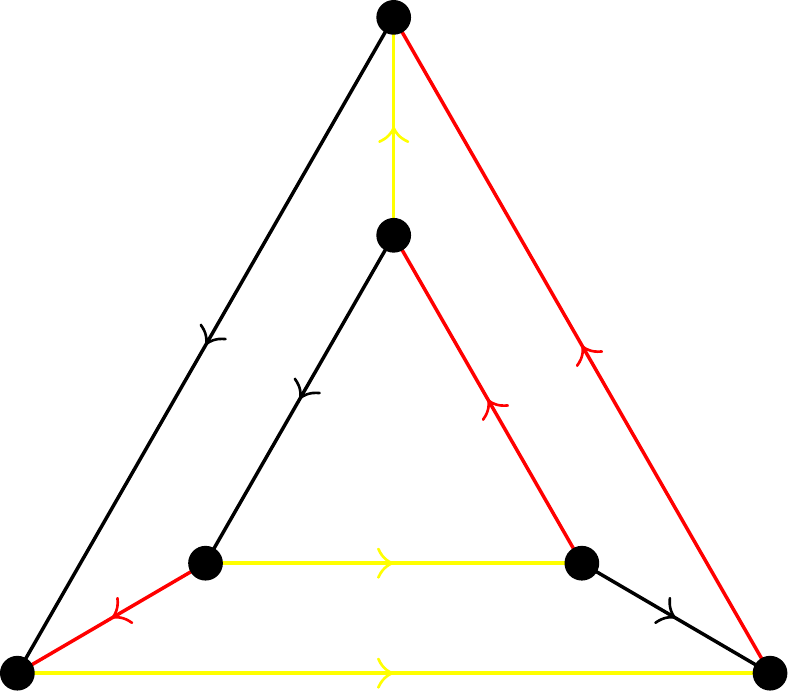
Pokiaľ potrebujete pomoc, tak skúste nájsť ekonomickú rovnováhu v krajine na nasledujúcom obrázku.

Zjavne tu ekonomická rovnováha vôbec nejde zaviesť, nakoľko mestá z vnútorného trojuholníka iba platia zvyšným mestám krajiny a tieto peniaze sa nemajú ako vrátiť späť pôvodným mestám. Teda riešenie tejto verzie úlohy pre \(n \ge 3\) je, že sa vo všeobecnosti ekonomická rovnováha nedá zaviesť, teda hľadané najmenšie \(k\) neexistuje. Nájsť príklady krajín pre \(n \ge 4\) prenechávame vám.

Keď si berieme najmenšie číslo, pre ktoré niečo ide, tak si musíme dať pozor, či tá vec vôbec ide – aby sme nevyberali najmenšie číslo z prázdnej množiny. Vo väčšine takýchto optimalizačných úlohách je zjavné, že nejaké riešenie existuje. No, ekonomická rovnováha je celkom komplikovaný pojem a pri tejto úlohe to až tak jasné nebolo.

Zaujímavosti o úlohe a zovšeobecnenia

Vrátime sa k našej verzii úlohy a povieme si o nej niečo viac. Skúsení riešitelia si isto všimli, že situáciu v zdaní možno opísať pomocou grafov. V teórii grafov dokonca existuje aj pojem, ktorý opisuje v grafe. Týmto pojmom je tok, ktorý priraďuje každej hrane číslo a orientáciu tak, aby pre každý vrchol grafu platilo, že súčet čísel na doňho vstupujúcich hranách je rovný súčtu čísel na vystupujúcich hranách. V samotnom toku môžu byť hranám priradené aj nuly. Pokiaľ je však každej hrane priradené nenulové číslo, hovoríme, že ide o nikde nulový tok. Ak navyše platí, že hranám sú priradené čísla z množiny \(\{1, 2, \dots, k-1\}\), tak hovoríme, že ide o nikde nulový \(k\)-tok (angl. nowhere-zero \(k\)-flow). Takže v reči teórie grafov bola táto úloha o hľadaní nikde nulového \(k\)-toku.

Pojem tok možno poznáte aj v inej súvislosti, asi hlavne z informatiky. Aby sme boli presný, ide o tok v sieti. Sieť je graf, ktorý má dva význačné vrcholy zdroj a stok a každá hrana má maximálnu kapacitu. Tok v sieti je potom podobné priradenie čísel a orientácií hranám s tým, že rovnosť súčtov na vchádzajúcich a vychádzajúcich hranách nemusí platiť pre zdroj a stok. Typickým problémom je nájsť taký tok, ktorý prepraví čo najväčšiu hodnotu od zdroja k toku. Toky v sietiach majú veľké uplatnenie v praxi. No my sa tu zaoberáme tokmi v grafoch. Tie majú síce ďalej od praxe, no ide o krajšiu kombinatorickú vlastnosť grafov. Závisia totiž iba od grafu samotného a nie od dvoch vrcholov navyše a kapacít hrán (čo je celkom dosť informácií).

Pozrime sa na to, čo sa stane, ak niektorú z podmienok v zadaní vypustíme. Začnime s tým, že odstránime predpoklad o zafarbení ciest. Takto však dostaneme, že pre väčšinu \(n\) nikde nulový tok nemusí vôbec existovať. Príkladom takých grafov sú grafy s mostom, čo je hrana grafu, ktorú keď z neho odstránime, tak sa rozpadne na dva komponenty, medzi ktorými sa nedá po hranách dostať. Takže, aby to bolo zaujímavé, tak budeme uvažovať len grafy, ktoré nemajú most. Stále však ostaneme pri grafoch, v ktorých z každého vrchola vychádzajú práve tri hrany. Takéto grafy sa nazývajú skrátene kubické.

Z toho už dostávame dosť zaujímavú úlohu, hľadať najmenšie \(k\), pre ktoré v kubickom grafe bez mostu existuje nikde nulový \(k\)-tok. Ukázali sme, že ak sa hrany kubického grafu dajú ofarbiť tromi farbami, tak obsahuje nikde nulový \(4\)-tok. Táto implikácia platí aj naopak: v kubickom grafe s nikde nulovým \(4\)-tokom sa dajú hrany ofarbiť tromi farbami tak, aby z každého vrchola vychádzali hrany rôznych farieb. Dôkaz vám prenechávame za cvičenie. Taktiež sa dá ľahko ukázať, kedy kubický bezmostový graf obsahuje nikde nulový \(3\)-tok. Je to práve vtedy, keď je bipartitný, teda keď sa dajú jeho vrcholy rozdeliť na dve časti tak, že každá hrana spája vrcholy z rôznych častí. Tiež si toto tvrdenie môžete skúsiť dokázať.

Ako teda s kubickými grafmi bez mostov, ktorých hrany sa nedajú zafarbiť tromi farbami? O existencii takýchto grafov sa dlho ani nevedelo. Prvý takýto graf bol bol objavený v roku 1898 Júliusom Petersenom a nesie po ňom názov Petersenov graf. Jeho objavenie vyvrátilo vtedajší nesprávny dôkaz (vtedy ešte) hypotéze o štyroch farbách. Nájdete ho na obrázku spolu s nikde nulovým \(5\)-tokom.

Dá sa v každom kubickom grafe bez mostu nájsť nikde nulový \(5\)-tok? Žiaľ, na túto otázku nie je známa odpoveď, ide o otvorený problém. Podarilo sa ukázať, že každý kubický graf bez mostu obsahuje nikde nulový \(6\)-tok, ale nie je známy žiaden kubický graf bez mostu, v ktorom by neexistoval \(5\)-tok.

A čo sa stane, ak upustíme od toho, že máme kubický graf? Nič až tak zaujímavé. Ak každý kubický graf bez mostu má nikde nulový \(k\)-tok, tak nikde nulový \(k\)-tok má aj ľubovoľný graf bez mostu. Toto si tiež môžete dokázať sami. Stačí si daný graf vhodne prerobiť na kubický tak, aby ste tok z kubického grafu vedeli prerobiť na tok v pôvodnom grafe.

Teda vidíme, že tento otvorený problém sa týka všetkých grafov bez mostov a pýta sa, či každý taký graf má nikde nulový \(5\)-tok. Prvý krát ho formuloval W. T. Tutte v roku 1954. Vidíme, že pri riešení tohto problému nám stačí uvažovať len kubické grafy. Tento otvorený problém sa radí medzi jedny z n