5. Päť minút romantiky vzorové riešenie

Táto úloha sa dala riešiť viacero možnými spôsobmi. Tu uvediem dva z nich. V prvom nájdeme trajektóriu Slnka po nebeskej sfére, a s využitím sférickej trigonometrie nájdeme uhol, pod akým Slnko zachádza za horizont. V druhom sa pozrieme na to, ako lokalita pozorovateľa prechádza cez pás polotieňa na Zemi.

Postup 1

V tomto postupe na zistenie toho, koľko bude slniečku trvať zapadanie, potrebujeme určiť tri veci:

1. Aké veľké je slniečko na oblohe,
2. Ako rýchlo ide po oblohe,
3. Pod akým uhlom bude zachádzať za horizont.

Trvanie západu potom bude čas, za aký slniečko na oblohe prejde vertikálnu vzdialenosť rovnú svojmu zdanlivému polomeru. Zachádzanie slnka za horizont je ilustrované na obrázku slniecko-zapada .

Pozrime sa teda na všetky tri záležitosti. Najprv ale ešte chcem pripomenúť, že všetky vzdialenosti aj rýchlosti, s ktorými tu budeme pracovať, nebudú dĺžkové vzdialenosti a rýchlosti, ale uhlové. To je preto, lebo Slnko, tak ako aj všetky ostatné objekty na oblohe, sa z pohľadu Zeme pohybuje po guli, ktorá sa v astronómii nazýva nebeská sféra, pričom Zem leží v strede tejto gule. No ale táto guľa je len imaginárna, a polohy objektov na nej sú len projekcie, takže vzdialenosti na nej nemá význam merať v dĺžkových jednotkách, význam majú len zlomky z celého obvodu gule, čo sú vlastne uhly. Inak povedané, guli môžete priradiť ľubovoľný polomer, vo výsledku sa aj tak vykráti.

Oboznámení s touto skutočnosťou sa môžeme pozrieť na pohyb Slnka po nebeskej sfére. Vieme, že zemská os je k rovine obehu naklonená. Na prvý pohľad sa vám preto možno zdá, že dráha Slnka po oblohe bude nejaká strašne komplikovaná. Pomocou malého triku ale uvidíte, že to tak vôbec nie je. Jediné, čo treba spraviť, je vrátiť sa do starých čias a prehlásiť Zem za nehybnú, a Slnko za jej obežnicu. Prejdeme teda do takej sústavy, v ktorej os Zeme smeruje kolmo nahor a ktorá sa otáča spolu so Zemou. Takýto prechod je znázornený na obrázku zmena-sustavy .

No a v tejto novej sústave je predsa pozorovateľ nehybný! To znamená, že na obrázku zmena-sustavy vidíme rovno dráhu, akú bude na oblohe opisovať Slnko. Už ju stačí iba nakloniť, keďže pozorovateľ stojí na obrázku naklonený.

Výsledok z prejdenia do novej sústavy teda je, že Slnko na oblohe opisuje kružnicu, ktorej stred je v smere severného pólu, ktorej uhlový polomer je \(\ang{90}-\delta\), a ktorá je naklonená o \(\phi\) voči horizontu. Teraz musíte veľmi silno zapojiť svoju predstavivosť. Výsledkom zapojenia vašej predstavivosti by mala byť situácia, ako znázornená na obrázku sfera-nebeska .

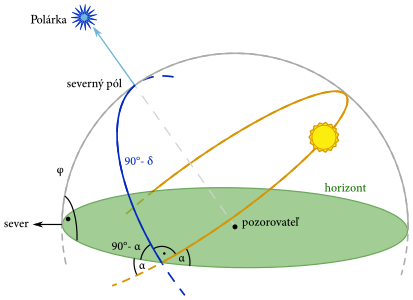
Naozaj, pokiaľ vám nebude jasná každá vec na tom obrázku, tak nečítajte ďalej. Čo sme na obrázku sfera-nebeska dostali, je demonštrácia geometrie na sfére. Čo to je zač? Rovnako ako v rovine existujú nejaké množiny bodov (kružnice, priamky,… ) a dajú sa nájsť pravidlá, ktoré musia útvary skonštruované z týchto množín spĺňať, to isté sa dá urobiť aj na povrchu gule. Napríklad jedno veľké odvetvie, sférická trigonometria, rieši trojuholníky na povrchu gule. A rovnako ako v rovine existuje Pytagorova veta, sínusová veta, atď., aj na guli existujú vzorčeky, ktoré mi zo znalosti nejakých parametrov trojuholníka umožnia vypočítať tie zvyšné. Nič viac, nič menej. Stačí si nalistovať na Wikipédii.

Najprv ale treba vlastne určiť, čo je trojuholník na guli. V rovine je trojuholník tvorený troma rovnými čiarami. Na guli ale nie sú rovné čiary. Ale skoro. Na guli sa považuje za rovnú čiaru to, čo človek dostane, keď nasadne do auta a ide stále rovno bez zatáčania volantom. Po čase sa samozrejme vráti na miesto, kde začal, takže zjavne nemohol ísť po rovnej čiare, ale je to to najrovnejšie, čo sa dá na guli dosiahnuť. Taká čiara sa volá hlavná kružnica.

Kontrolná otázka: Ktoré z čiar na obrázku sfera-nebeska sú rovné?

Odpoveď: Modrá, horizont, a obrys znázorňujúci oblohu. Dráha slnka nejde po hlavnej kružnici.

Nechce už veľa ďalšej námahy uvedomiť si, že rovnú čiaru na guli tvorí vždy kružnica so stredom v strede gule. Nám sa teda ponúka nejaký ten trojuholníček. Napríklad trojuholník sever – severný pól – bod západu Slnka. Už zostáva len nalistovať si v nejakej múdrej internetovej stránke. Jedna z prvých vecí, čo tam na vás vyskočí, je asi sínusová veta. Táto veta je skoro úplne rovnaká ako pre rovinné trojuholníky, len treba brať aj sínusy dĺžok strán.¹ Pre náš prípad teda bude \[ \frac{\sin\phi}{\sin\left(\ang{90} - \alpha\right)} = \frac{\sin\left(\ang{90} - \delta\right)}{\sin \ang{90}}, \]

a keďže \(\sin\left(\ang{90} - x\right) = \cos x\), tak máme \[ \cos\alpha = \frac{\sin\phi}{\cos\delta}. \qquad(1)\]

Bod číslo 3 hotový! Teraz bod číslo 2. Je jasné, že Slnko musí celú svoju dráhu na oblohe opísať za 24 hodín. Ak je uhlový priemer kružnice \(\ang{90} - \delta\), pri pohľade na obrázok zmena-sustavy je zrejmé, že jeho polomer je \(\sin\left(\ang{90} - \delta\right) = \cos\delta\), a teda dĺžka \(2\pi\cos\delta\). Tak dostávame uhlovú rýchlosť slniečka na oblohe \[ \omega = \frac{2\pi \cos\delta}{\SI{24}{\hour}}. \qquad(2)\]

Už zostáva len bod číslo jedna – nájsť uhlovú veľkosť Slnka. Tu nie je nad čím rozmýšľať, len pozrieť sa na internet, kde sa dočítame, že je rovný približne 32 uhlových minút \(=2\pi\cdot\frac{32}{360 \cdot 60} = \SI[parse-numbers = false]{\frac{2\pi}{675}}{\radian}\).² Ďalej ho označím \(d\). A už len stačí to všetko dať dokopy – podľa obrázku slniecko-zapada potrebujeme, aby Slnko prešlo vzdialenosť \[ x = \frac{d}{\sin\alpha}. \qquad(3)\]

Teraz už môžete buď do vzorcov 1, 2 a 3 podosádzať čísla a tak dostať výsledok, alebo ich skombinovať a vyjadriť výsledok vo všeobecnosti. Všeobecný výsledok pre trvanie západu slnka je \[ t = \frac{x}{\omega} = \SI{24}{\hour}\cdot\frac{d}{2\pi\sin\left(\arccos\left(\frac{\sin\phi}{\cos\delta}\right)\right)\cos\delta} = \frac{\SI{24}{\hour}}{675}\cdot\frac{1}{\sqrt{\cos^{2}\delta-\sin^{2}\phi}} = \SI{128}{\second}\cdot\frac{1}{\sqrt{\cos^{2}\delta-\sin^{2}\phi}}, \] kde sme využili, že \(\sin=\sqrt{1-\cos^{2}x}\).

Aký utešený výsledok! Pamätajte, že \(\delta\) je uhol dopadajúcich lúčov voči zemskej osi a \(\phi\) je zemepisná šírka pozorovateľa na Zemi. Čo sa týka rovnodennosti, vtedy je uhol \(\delta\) rovný nule a náš vzorček nám dá výsledok \(\num{191.29}\) sekundy = 3 min. 11 s. Čo sa týka slnovratov, počas zimného aj letného je uhol \(\delta\) rovný náklonu zemskej osi voči rovine obehu, a to je \(\ang{23.44}\), a náš vzorček dá výsledok \(\num{237.90}\) sekundy = 3 min. 58 s. Vidíme teda, že počas rovnodenností je západ Slnka najkratší a počas slnovratov najdlhší, a v iných časoch roka osciluje medzi nimi.

Ny záver si treba uvedomiť, že v riešení sme urobili jednu aproximáciu – predpokladali sme z obrázka slniecko-zapada , že slnko sa počas zapadania pohybuje po priamke, čo ale nie je pravda, keďže Slnko sa na oblohe pohybuje po kružniciach, čo sme si tak krvopotne uvedomovali, a teda dráha na obrázku slniecko-zapada je v skutočnosti len malý úsek kružnice. Ten ale môžeme považovať za priamku, keďže uhlový priemer Slnka je oveľa menší, ako dĺžka celej jeho dráhy po oblohe. Akurát v polárnych krajoch by bol náš výsledok značne nepresný a museli by sme to počítať inak.

Už len dodám, že obrázok sfera-nebeska je kľúčom k pochopeniu všetkých javov súvisiacich s pohybom slnka počas roka na oblohe. Skúste si napríklad premyslieť, ako by sa tento obrázok vyvíjal v čase pre nejaké fixné miesto na zemi (fixné \(\phi\), premenlivé \(\delta\)), alebo ako by vyzeral pre miesto, kde práve prebieha polárny deň alebo noc.

Postup 2

V tomto postupe bude kľúčové uvedomiť si, že počas zapadania slnka prechádzjú Vladko s Katkou cez rozhranie medzi dennou a nočnou stranou zeme. To je pás čiastočného tieňa, ktorý sa tiahne okolo celej Zeme, a miesta ktoré sa v ňom práve nachádzajú, práve zažívajú západ/východ Slnka. Krátke zamyslenie nás privedie k záveru, že šírka tohoto pásu musí byť rovná uhlovému priemeru Slnka. Ďalej sa na celú situáciu môžeme pozerať v projekcii z boku, tak že pás polotieňa je vertikálny a dráha Vladka s Katkou ide vzhľadom na polotieň pod uhlom \(\delta\). Celý pohyb sa takto efektívne odohráva v rovine, nám stačí zobrať len správne zložky rýchlostí a vzdialeností, a určiť, koľko potrvá cesta Vladka s Katkou cez pás polotieňa. Všetko je znázornené na obrázku pohlad-z-boku .

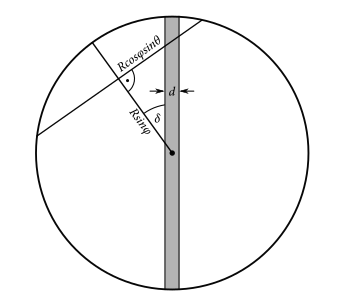
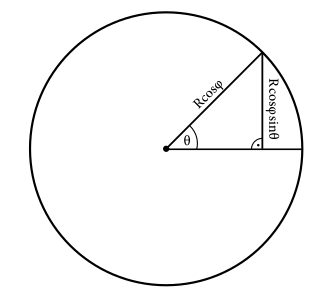
Dôležité pozorovanie ešte je, že rýchlosť Vladka s Katkou premietnutá do roviny je úmerná kosínusu uhla \(\theta\) medzi nimi a smerom kolmým na rovinu projekcie. Ak idú Vladko s Katkou po rovnobežke so zemepisnou šírkou \(\phi\), tak ich skutočná obežná rýchlosť je \(\omega\cos\phi\) a teda zložka v smere roviny je \[ \omega\cos\phi\cos\theta, \] kde \(\omega\) je uhlová rýchlosť otáčania Zeme. Nás teda zaujíma uhol \(\theta\) v momente, keď Vladko s Katkou prechádzajú cez pás. Na to, aby sme pochopili, kde sa na obrázku pohlad-z-boku vzala dĺžka \(R\cos\phi\sin\theta\), nám pomôže, ako inak, obrázok rovnobezka-z-hora . Ten ilustruje pohľad zhora na rovnobežku, po ktorej sa dvojica pohybuje.

Teraz z geometrie pravouhlého trojuholníka na obrázku pohlad-z-boku vyplýva \[ \tan\delta=\frac{R\cos\phi\sin\theta}{R\sin\phi}, \] odkiaľ vyjadríme uhol \(\theta\)

\[ \theta=\arcsin\left(\tan\delta\tan\phi\right). \] A už to stačí len dať dokopy. Podľa obrázka pohlad-z-boku musia Vladko s Katkou cez pás prejsť vzdialenosť \[ \frac{d}{\cos\delta} \] a to rýchlosťou \[ \omega\cos\phi\cos\left(\arcsin\left(\tan\delta\tan\phi\right)\right). \] Teda čas, ktorý na to potrebujú, je \[ T=\frac{d}{\omega\cos\delta\cos\phi\cos\left(\arcsin\left(\tan\delta\tan\phi\right)\right)}. \] Opäť využijeme že \(\cos x=\sqrt{1-\sin^{2}x}\) a dostaneme \[ T=\frac{d}{\omega\sqrt{\cos^{2}\delta\cos^{2}\phi-\sin^{2}\delta\sin^{2}\phi}}. \] Teraz už len stačí znova napísať \(\cos^{2}\phi\) v prvom člene ako \(1-\sin^{2}\phi\) a \(\sin^{2}\delta\) v druhom ako \(1-\cos^{2}\delta\), a dostávame \[ T=\frac{d}{\omega\sqrt{\cos^{2}\delta-\sin^{2}\phi}}, \] čo je rovnaký výsledok, ako predchádzajúcou metódou :)