Zadanie
Zakiaľ, čo sa uhorský princ Ákos zabával Jakubovými slávnymi číslami, potajme vyvíjal jeho úhlavný nepriateľ Kazisvet Matúš Strašný všemohúci trebuchet. Takýto katapult by navždy rozmetal kráľovské mestské steny a vyhnal Kiku z Uhorského kráľovstva. Problém však nastal, keď sa zistilo, že takýto mocný katapult možno postaviť iba na špeciálnej \(n\)-uholníkovej podstave.
Nájdite všetky celé čísla \(n \ge 3\), pre ktoré existuje \(n\)-uholník, ktorý:
má celočíselné dĺžky strán;
každé jeho dve susedné strany sú na seba kolmé;
nedá sa celý pokryť neprekrývajúcimi sa dlaždicami rozmeru \(1 \times 2\), ktorých strany sú rovnobežné so stranami \(n\)-uholníka (otáčať ich možno).
Najprv sa zamyslime koľko-uholníky spĺňajú prvé dve vlastnosti. Pre súčet vnútorných uhlov \(n\)-uholníka platí, že je rovný \((n-2) \cdot 180^\circ\). 1 Strany \(n\)-uholníkovej podstavy katapultu majú byť na seba kolmé. Teda každý vnútorný uhol podstavy katapultu musí byť buď \(90^\circ\) alebo \(270^\circ\). Majme \(k\) vnútorných uhlov s veľkosťou \(270^\circ\) a \((n-k)\) vnútorných uhlov s veľkosťou \(90^\circ\) (pretože spolu máme \(n\) vnútorných uhlov). Ak takýto \(n\)-uholník existuje, tak musí platiť rovnosť: \((n-2) \cdot 180^\circ = k\cdot 270^\circ + (n-k)\cdot90^\circ\). To vieme jednoducho upraviť na tvar \(2n - 4 = n + 2k\). Môžeme si všimnúť, že výraz na ľavej strane je vždy párny. Výraz na pravej strane je párny práve vtedy, keď \(n\) je párne. Teda táto rovnosť môže platiť len pre párne \(n\), čo znamená, že podstava katapultu môže mať len párny počet strán.
Teraz skúsme hľadať konkrétne \(n\)-uholníkové podstavy, ktoré spĺňajú aj tretiu vlastnosť. Ak \(n=4\), tak si môžeme zobrať štvorec veľkosti \(1 \times 1\) a ten rozhodne nejde pokryť dlaždicami s rozmermi \(1 \times 2\). Ďalej môžeme hľadať \(6\), \(8\), \(10\) a viac uholníky a podarí sa nám nájsť napr. takéto „schodíkové podstavy“:
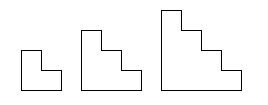
Po troške skúšania a ukladania dlaždičiek nadobudneme dojem, že keď je najmenšia strana dĺžky \(1\), tak to naozaj nepôjde vydláždiť. Už to len treba dokázať. Pri úlohách s dláždením sa nám mnohokrát oplatí vyfarbiť si políčka. Bude tomu tak aj v tejto úlohe. Vyfarbime štvorčeky ako políčka šachovnice, teda striedavo na bielo a na čierno. Môžeme to vidieť aj na obrázku.
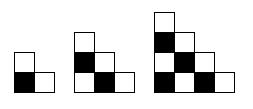
Dlaždica rozmerov \(1 \times 2\) zakryje dva susedné štvorce, teda jeden biely a jeden čierny. Vidíme, že všetky pravé horné štvorčeky (štvorčeky, ktoré tvoria najdlhšiu diagonálu) sú biele. Štvorčeky, ktoré s nimi susedia (štvorčeky pod nimi) sú všetky čierne. Každá dlaždička, ktorá nám zakryje horný biely štvorček musí zakryť, ešte susediaci čierny štvorček. Tých je však o \(1\) menej. Z toho vyplýva, že takéto schodíky sa nedajú pokryť dlaždicami \(1 \times 2\). Takéto podstavy spĺňajú všetky tri vlastnosti. Hľadané \(n\) sú všetky párne čísla, až na číslo \(2\). Mohli by sme aj zamyslieť nad počtom bielych a čiernych štvorčekov. Čiernych je vždy menej. (Rozmyslite si.) Z toho znova vyplýva, že takéto schodíky sa nedajú pokryť dlaždicami \(1 \times 2\) a hľadanými \(n\) sú všetky párne čísla okrem čísla \(2\).
Skúste si rozmyslieť, že toto naozaj platí aj pre nekonvexné mnohouholníky.↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.