Zadanie
Templár Slavomír, vracajúci sa zo zemí saracénskych domov, si nemohol nevšimnúť krivosť mestských stien. Ako povinnosť káže, ihneď o tom upovedomil svoju kráľovnú Kiku. Tú to tak vyviedlo z miery, až prikázala svojmu najlepšiemu architektovi Mirovi, aby hradby zdemoloval (v tom je on expert) a nahradil ich najnovším typom trojcípich hradieb stojacich na špeciálnej trojuholníkovej sieti.
Rovnostranný trojuholník so stranou dĺžky \(n\) je rozdelený na \(n^2\) rovnostranných trojuholníkov so stranou dĺžky \(1\). Miro si vyberie niekoľko z týchto trojuholníkov tak, aby sa po stranách vybraných trojuholníkov dalo prejsť medzi ľubovoľnými dvoma z nich. Následne postaví hradby na úsečkách medzi vybranými a nevybranými trojuholníkmi a tiež medzi vybranými trojuholníkmi a obvodom veľkého trojuholníka. Koľko rôznych počtov trojuholníkov si môže vybrať, ak celková dĺžka hradieb musí byť presne \(3n\)? Na obrázku môžete vidieť príklad možného výberu trojuholníkov, ktorý vyhovuje podmienkam.
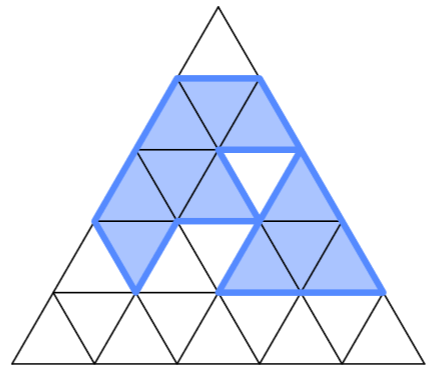
Riešenie takejto úlohy sa delí na dve časti. Najskôr dokážeme, že to nejde pre nejaké počty trojuholníkov a potom ukážeme, že všetky ostatné počty trojuholníkov vyhovujú, teda že existuje vhodný výber trojuholníkov.
Najskôr si môžeme všimnúť, že potrebujeme aspoň \(n\) trojuholníkov. Každý trojuholník môže prispieť najviac tromi hradbami. Teda aby sme mali \(3n\) hradieb, potrebujeme aspoň \(n\) trojuholníkov. Najviac ich môžeme mať \(n^2\), čo je počet malých trojuholníkov v celom veľkom trojuholníku.
Ukážeme, že všetky možné počty ktoré si Miro môže vybrať, sú presne tie, pre ktoré platí :
počet trojuholníkov je väčší alebo rovný \(n\)
počet trojuholníkov je menší alebo rovný \(n^2\)
počet trojuholníkov má tú istú paritu ako \(n\) a \(n^2\)
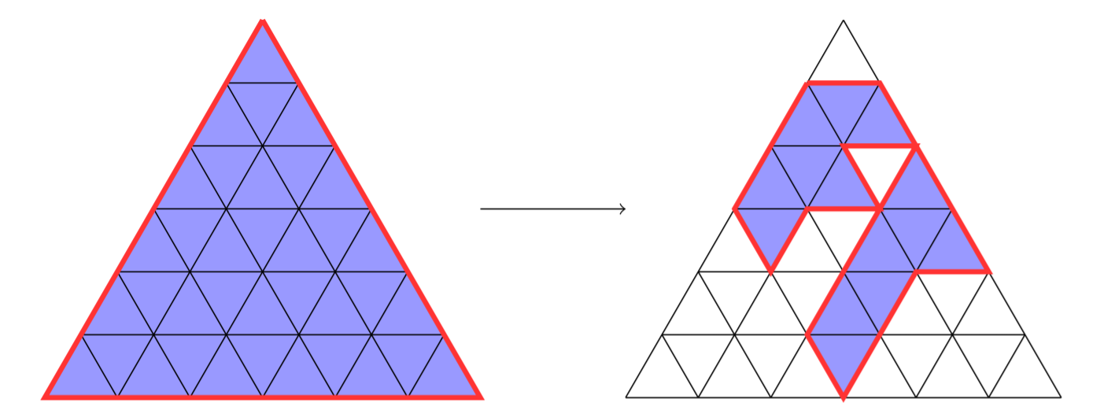
Tu máme jednu možnosť pre \(n=6\) ako si môžeme vybrať \(14\) trojuholníkov tak aby sme mali \(18\) hradieb.
Predstavme si, že nazačiatku sú vybraté všetky trojuholníky a my ich postupne budeme odoberať tak, aby ostali vybraté tie, ktoré chceme. Na predchádzajúcom obrázku sme odobrali všetky trojuholníky, ktoré už nie sú vyfarbené. Toto odoberanie trojuholníkov môžeme robiť postupne, vždy po jednom trojuholníku. V každom kroku tohto odoberania trojuholníkov máme 4 možnosti ako sa celkový počet hradieb môže zmeniť:
Ak odobratý trojuholník (na obrázku vždy stredný trojuholník) má všetky \(3\) strany spoločné s vybranými trojuholníkmi, keď odoberieme tento trojuholník, budeme mať o \(3\) hradby viac.
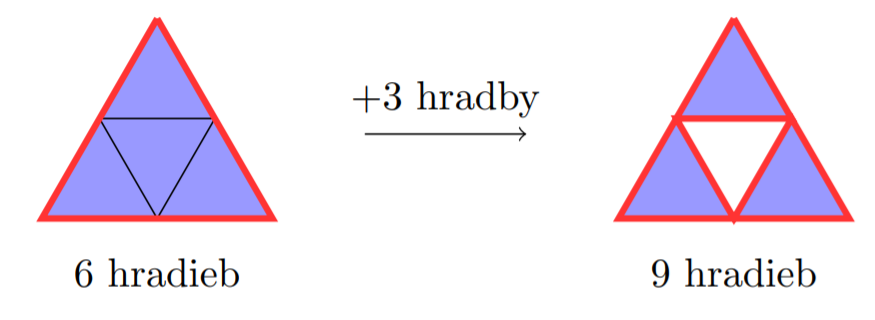
Ak odobratý trojuholník má \(2\) strany spoločné s vybranými trojuholníkmi, keď odoberieme tento trojuholník, budeme mať o \(1\) hradbu viac.
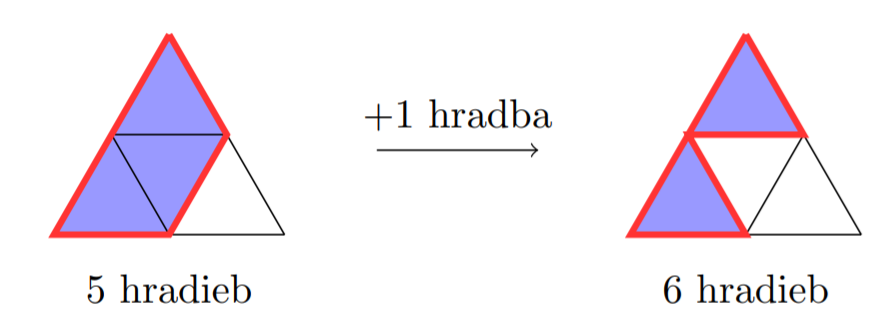
Ak odobratý trojuholník má \(1\) stranu spoločnú s iným vybraným trojuholníkom, keď odoberieme tento trojuholník, budeme mať o \(1\) hradbu menej.
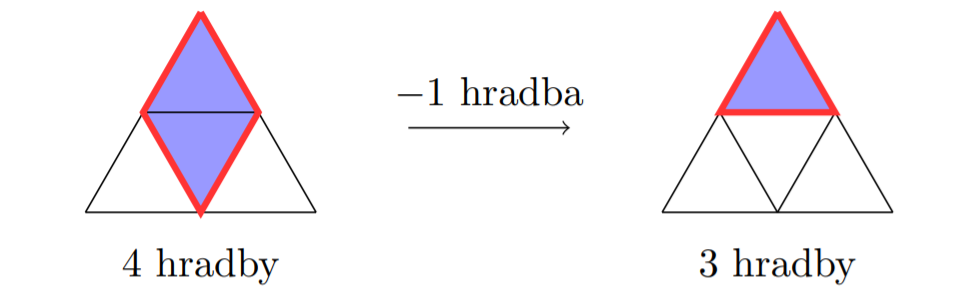
Ak odobratý trojuholník nemá žiadnu stranu spoločnú s iným vybraným trojuholníkom, keď odoberieme tento trojuholník, budeme mať o \(3\) hradby menej.
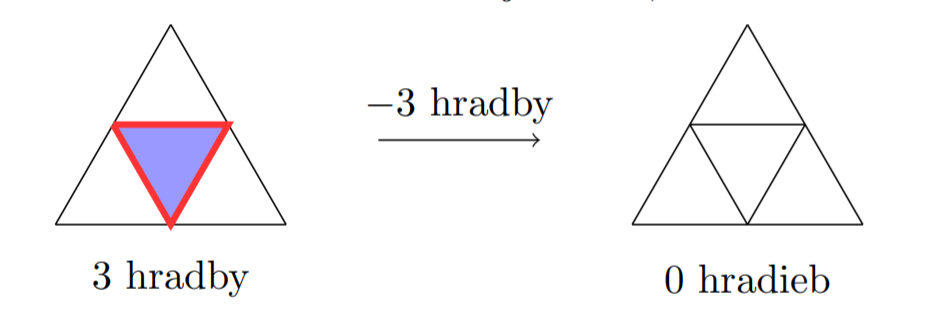
Poznamenajme, že aj keď odoberáme malý trojuholník na kraji alebo v rohu veľkého trojuholníka, počet hradieb sa bude meniť rovnako ako na predchádzajúcich obrázkoch. Podľa toho s koľkými vybranými trojuholníkmi odoberaný trojuholník susedil.
Všimnime si, že vždy zmeníme počet hradieb o nepárne číslo, takže parita počtu hradieb sa zmení zakaždým ako odoberieme jeden trojuholník. Teda aby sme sa vrátili k \(3n\) hradbám rovnako ako sme mali nazačiatku procesu, musíme meniť paritu párny počet krát, teda odobrať párny počet trojuholníkov. Môžu nám teda ostať len tie počty trojuholníkov, ktoré sú medzi \(n\) a \(n^2\) a majú tú istú paritu ako \(n^2\). Ešte treba dokázať, že môžeme dosiahnuť všetky tieto počty.
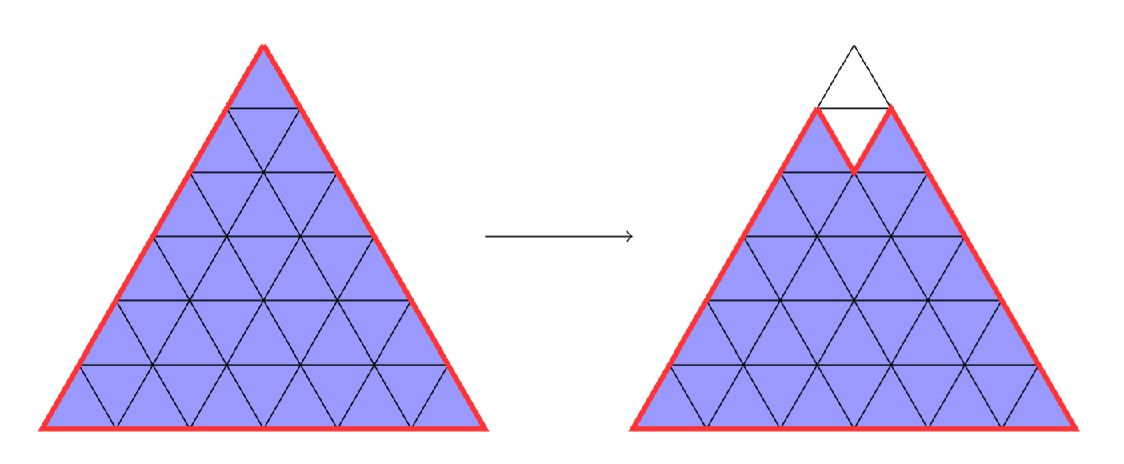
Na to stačí nájsť nejaký postup ktorým dostaneme všetky tieto možnosti. Začneme s \(n^2\) trojuholníkmi. V prvom kroku odoberieme \(2\) horné trojuholníky a zostane nám stále \(3n\) hradieb.
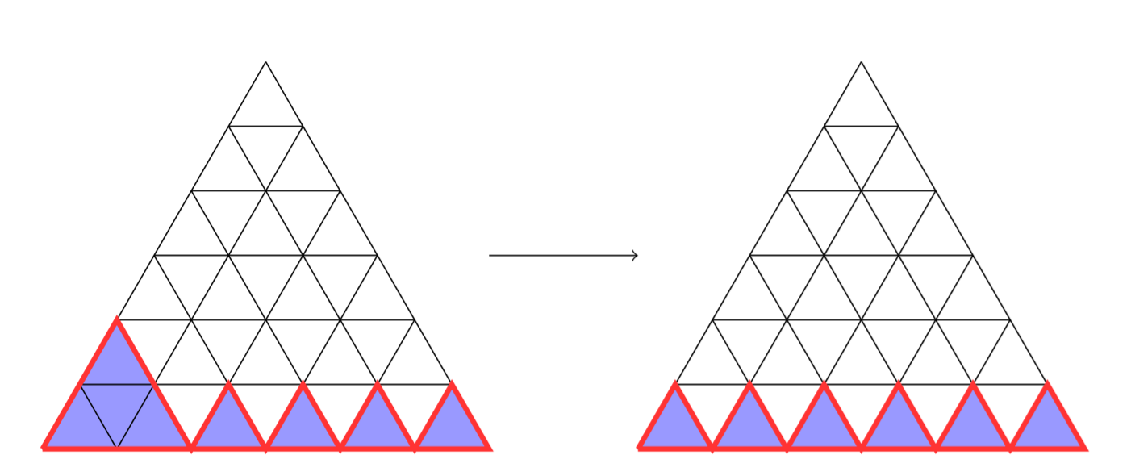
Pokračujeme tým istým spôsobom, budeme odoberať \(2\) trojuholníky v tvare kosoštvorca a zostane nám \(3n\) hradieb po každom kroku. Tento proces sa skončí, keď nám zostane \(n\) trojuholníkov. Posledný krok bude vyzerať takto :
Všetky možné počty trojuholníkov ktoré si Miro môže vybrať sú teda všetky počty tej istej parity ako je \(n\) a \(n^2\) medzi \(n\) a \(n^2\).
To je \(\displaystyle \frac{n^2-n}{2} + 1\) možných počtov trojuholníkov.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.