Zadanie
Po vojne je každý generálom. O to horšie, keď nemáte generála ani pred bitkou. To bol nakoniec i dôvod neslávneho konca tureckej armády, ktorá nedokázala odolávať nájazdom uhorských koníkov. Na počesť tohto veľkolepého víťazstva sa Uhori rozhodli na bojisku vztýčiť víťazný stĺp, ktorý by bol symbolom tohto veľkolepého víťazstva pre mnohé generácie. Ukázalo sa však, že vztýčiť víťazný stĺp len tak uprostred bojiska je omnoho ťažšie, ako sa predpokladalo a na jeho vztýčenie bude potrebných kopec obskúrnych prerekvizít. Veď usúďte sami:
Nech \(ABCD\) je lichobežník, kde \(AB \parallel CD\), \(|AB| > |CD|\) a \(|BC| = |CD| = |DA|\). Body \(E\) a \(F\) delia stranu \(AB\) na tri rovnako dlhé časti s tým, že bod \(E\) je medzi bodmi \(A\) a \(F\). Priamky \(CF\) a \(DE\) sa pretínajú v bode \(P\). Dokážte, že \(|\sphericalangle APB| = |\sphericalangle DAB|\).
Hneď na prvý pohľad nám môže byť podozrivé (keď si zakreslíme všetky priamky a uhly spomínané v zadaní), že bod \(P\) je spojený \(4\)-mi úsečkami so všetkými zadanými bodmi. Dokonca na dvoch z nich je tých bodov viac. Zároveň všetky tieto body ležia na dvoch rovnobežných priamkach. Vďaka tomu máme podobné trojuholníky \(PEF\) a \(PDC\), o ktorých navyše vieme, že strana \(CD\) je rovnobežná so stranou \(EF\) a zároveň \(|EF|=|AE|=|FB|\). Skúsenejším by to už mohlo napovedať, že narazili na rovnoľahlosť z bodu \(P\).
Tak si skúsme predĺžiť aj úsečky \(PA\) a \(PB\) tak, aby sa preťali s priamkou \(CD\). Ich priesečníky označme postupne \(G\) a \(H\). Tým dostaneme niekoľko dvojíc podobných (rovnoľahlých) trojuholníkov, medzi nimi aj dvojice trojuholníkov \(PAE\), \(PGD\) a \(PBF\), \(PHC\). Ľahko ukážeme, že koeficient podobnosti všetkých troch spomínaných dvojíc je rovnaký. Preto keď platí \(|AE|=|EF|=|FB|\), tak potom aj \(|GD|=|DC|=|CH|\).
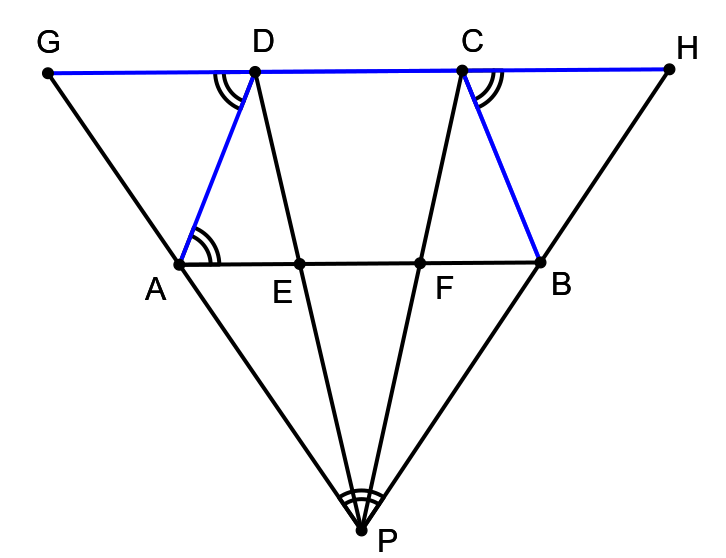
Vďaka tomu sú trojuholníky \(ADG\) a \(BCH\) rovnoramenné. Keďže lichobežník je tiež rovnoramenný, máme \(|\sphericalangle ADC|=|\sphericalangle BCD|\), preto platí aj \(|\sphericalangle ADG|=|\sphericalangle BCH|\). Vďaka tomu vieme, že trojuholníky \(ADG\), \(BCH\) sú zhodné.
To nám zároveň hovorí, že \(|\sphericalangle AGD|=|\sphericalangle BHC|\), preto trojuholník \(GPH\) je tiež rovnoramenný a podobný s trojuholníkmi \(ADG\) a \(BCH\). Z podobnosti máme \(|\sphericalangle ADG|=|\sphericalangle GPH|\). Už iba posledný krok, uhly \(ADG\) a \(DAB\) sú striedavé, preto \(|\sphericalangle DAB|=|\sphericalangle ADG|=|\sphericalangle APB|\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.
Samuel Stanek
Nejak neviem, ako z toho, že uhol AGD = BHC vyplýva, že trojuholník GPH je podobný s ADG a BCH?
Štefánia Glevitzká
Ukázali sme, že trojuholníky $ADG$ a $BCH$ sú zhodné a rovnoramenné. Preto $|\sphericalangle GAD|=|\sphericalangle AGD|=|\sphericalangle BHC|$. Oba trojuholníky majú po dva uhly tejto veľkosti. No uhly $AGD$ a $BHC$ sú aj vnútornými uhlami trojuholníka $GPH$, preto je trojuholník $GPH$ podobný s trojuholníkmi $ADG$ a $BCH$ podľa vety uu.