Zadanie
Mesto odolalo obliehaniu. Matúš pokušeniu vyhodiť svojich neschopných generálov zo skupiny. A Ákos nutkaniu zastaviť sa cestou z bojiska v najbližšom mäsiarstve po klobásku. Tak sa stalo, že všetko toto sa stretlo na jednej kope a všetci žili v obliehaní, síce nie šťastní, ale aspoň dokým nepomreli. Mesto obkľúčili Mirove hradby, ktoré obkľúčil Matúš, ktorého obkľúčila Ákosova armáda. A pletky s kružnicami sa mohli začať.
Dané sú kružnice \(k_1\) a \(k_2\), ktoré majú stredy \(O_1\) a \(O_2\) a ktoré sa pretínajú v bodoch \(A\) a \(B\). Priamka \(O_1A\) pretína \(k_2\) v bodoch \(A\) a \(C\) a priamka \(O_2A\) pretína \(k_1\) v bodoch \(A\) a \(D\), pričom \(A\) je vnútorným bodom úsečiek \(O_1C\) aj \(O_2D\). Priamka rovnobežná s priamkou \(AD\), ktorá prechádza cez bod \(B\) pretína \(k_1\) v bodoch \(B\) a \(E\). Predpokladajme, že priamky \(AC\) a \(DE\) sú navzájom rovnobežné. Dokážte, že priamka \(CD\) je kolmá na priamku \(CO_2\).
Príprava pred úlohou. Plán útoku na túto úlohu bude nasledovný, dokážeme, že \(O_1,O_2,C,D\) ležia na kružnici. Potom dokážeme, že \(|\sphericalangle DCO_1| + |\sphericalangle O_1CO_2| = 90^\circ\). Na to však využijeme niektoré poznatky z geometrie, ktoré bez dôkazov sformulujeme do Lemy 1 a Lemy 2. Dôkazy si môžete skúsiť spraviť na domácu úlohu. :)
Lema 1. Majme kružnicu \(k\) a v nej dve rovnobežné tetivy \(t_1\) a \(t_2\), potom body \(A,B \in k \cap t_1; A\neq B\) a \(C,D \in k\cap t_2; C\neq D\) tvoria rovnoramenný lichobežník.
Lema 2. Predpokladajme, že body \(Y, Z\) ležia v tej istej polrovine danej priamkou \(WX\). Potom body \(W,X,Y,Z\) ležia na kružnici práve vtedy, keď platí \(|\sphericalangle WYX|=|\sphericalangle WZX|\).
Riešenie. Označme \(|\sphericalangle ACO_2| = \alpha\). Keďže trojuholník \(ACO_2\) je rovnoramenný, tak aj \(|\sphericalangle O_2AC| = \alpha\). Potom aj \(|\sphericalangle DAO_1| = \alpha\), pretože, sa jedná o vrcholové uhly. Taktiež vieme, že trojuholník \(O_1AD\) je rovnoramenný s ramenami \(O_1A\) a \(O_1D\). Teda aj \(|\sphericalangle O_1DA|= \alpha\) a z rovnosti \(|\sphericalangle ACO_2| = \alpha = |\sphericalangle O_1DA|\) vidíme, že body \(O_1,O_2,C,D\) vďaka Leme 2 ležia na kružnici. Ešte podotkneme, že body \(C,D\) vskutku ležia v tej istej polrovine danej priamkou \(O_1,O_2\).
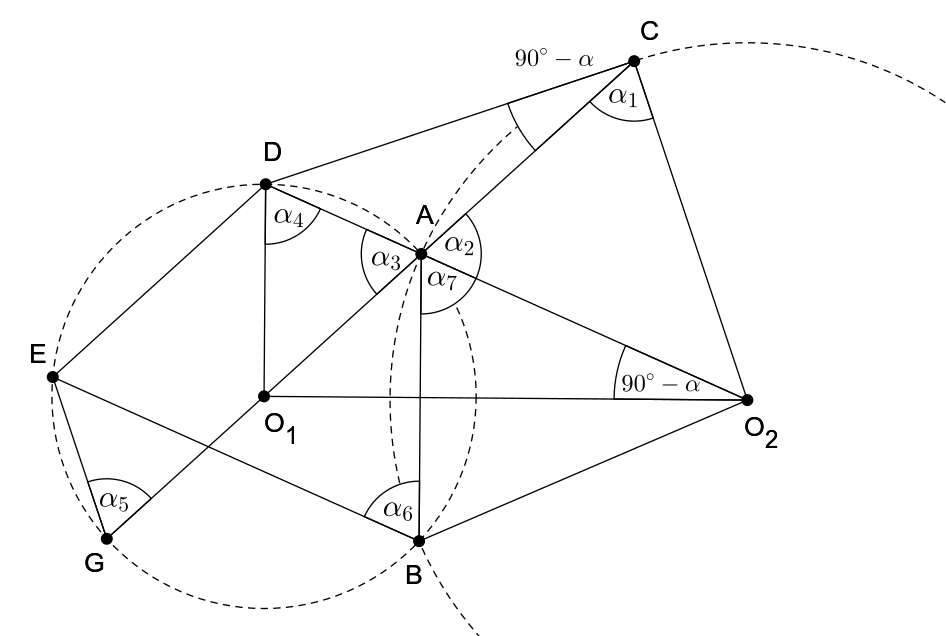
Dodefinujme bod \(G\) ako druhý priesečník priamky \(AO_1\) s kružnicou \(k_1\). Keďže tetivy \(GA\) a \(ED\) sú rovnobežné tak podľa Lemy 1 je \(GADE\) rovnoramenný lichobežník, a preto platí pre uhly \(|\sphericalangle DAG|=|\sphericalangle AGE|=\alpha\). Ďalej, keďže body \(AEGB\) ležia na kružnici tak musí taktiež platiť, že \(|\sphericalangle AGE|=|\sphericalangle ABE|=\alpha\). Keďže priamky \(O_2D\) a \(BE\) sú rovnobežné (zo zadania), tak uhly \(|\sphericalangle ABE|=|\sphericalangle BAO_2|=\alpha\). A nakoniec, keďže \(AO_2B\) je rovnoramenný trojuholník tak \(|\sphericalangle AO_2B|= 180^\circ -2\alpha\).
Je známe, že spojnica \(AB\) je rozpolená spojnicou stredov kružníc \(O_1O_2\) a preto uhol \(|\sphericalangle AO_2O_1|=90^\circ - \alpha\). No ale z tetivovosti \(O_1O_2CD\) je jasné, že aj \(|\sphericalangle O_1CD|=90^\circ -\alpha\). A teraz si spomenieme, že na začiatku sme si povedali, že \(|\sphericalangle ACO_2| = \alpha\), takže dokopy, \(|\sphericalangle O_1CD| + |\sphericalangle ACO_2| = 90^\circ - \alpha + \alpha = 90^\circ\). Čo je to, čo sme chceli dokázať.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.