Zadanie
S doplnenými zásobami sa hneď plaví lepšie. Niet preto divu, že Magalhães svižne oboplával Patagóniu, až sa dostal k zvláštnemu lichobežníkovému súostroviu. Pomôžte mu zistiť, pod akým uhlom sa má teraz vydať, aby bezpečne preplával medzi ostrovmi.
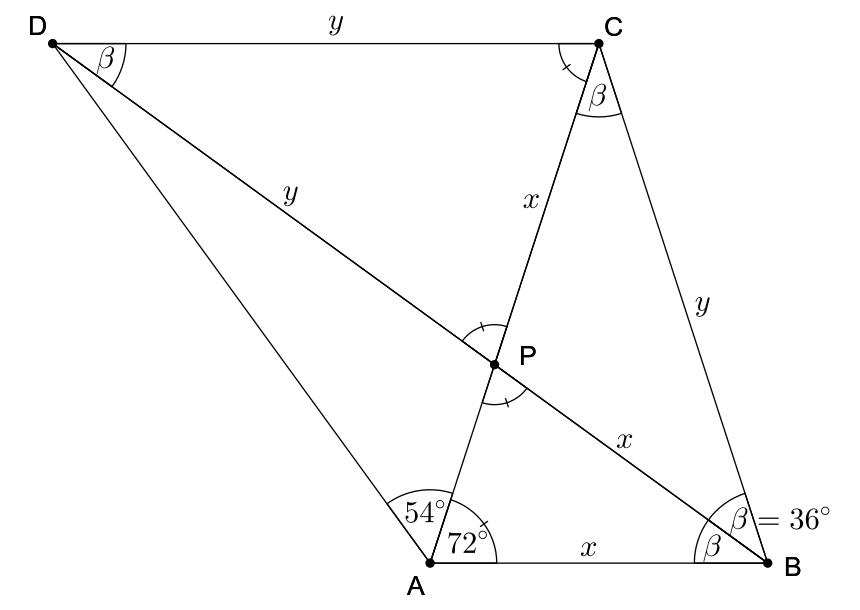
Je daný lichobežník \(ABCD\) so základňami \(AB\) a \(CD\), ktorého uhlopriečky sa pretínajú v bode \(P\). Vieme, že platí \(|BC|=|DP|\) a \(|AB|=|CP|\). Navyše \(BD\) je osou uhla \(ABC\). Vypočítajte veľkosť uhla \(DAB\).
Našou úlohou je vypočítať veľkosť uhla \(BAC\). Podľa zadania vieme, že niektoré dĺžky úsečiek sú rovnaké. Rovnosť dĺžok budeme chcieť neskôr použiť, pre ľahšie odkazovanie sa, si označme \(x,y\), pre \(x=|AB|=|CP|\) a \(y=|BC|=|DP|\). Taktiež určite budeme chcieť použiť, že priamka \(BD\) je osou uhla \(ABC\), preto si tiež označme \(\beta=\left| \sphericalangle ABD \right |=\left| \sphericalangle DBC \right |\). Pozrime sa, kde všade sa uhol \(\beta\) nachádza a aké všetky uhly možno pomocou neho vyjadriť.
Vďaka rovnobežkám \(AB\) a \(CD\) sú uhly \(ABD\) a \(BDC\) striedavé, čo znamená \(\left| \sphericalangle BDC \right |=\left| \sphericalangle ABD \right |=\beta\). Všimnime si, že v trojuholníku \(BCD\) sa \(\beta\) vyskytuje dvakrát, takže trojuholník je rovnoramenný. Vďaka tomu \(|CD|=|BC|=y\), a teda aj trojuholník \(CDP\) je rovnoramenný s uhlom \(\beta\) pri vrchole \(D\), preto pre uhly pri základni platí \(\left| \sphericalangle DCP \right |=\left| \sphericalangle DPC \right |=90^\circ - \frac \beta 2\). Zároveň je k nim uhol \(BAP\) striedavý a uhol \(BPA\) vrcholový, preto aj \(\left| \sphericalangle BAP \right |=90^\circ - \frac \beta 2=\left| \sphericalangle BPA \right |\). Tým znova dostávame rovnoramenný trojuholník \(BPA\), kde \(|BP|=|BA|\). Keďže aj \(|AB|=|CP|\), máme rovnoramenný trojuholník \(BCP\), \(\left| \sphericalangle BCP \right |=\left| \sphericalangle CBP \right |=\beta\).
Predchádzajúcimi úvahami sa nám podarilo vyjadriť väčšinu uhlov v obrázku pomocou uhla \(\beta\). Keď sa pozrieme, čo všetko sme pomocou uhla \(\beta\) vyjadrili, tak si môžeme všimnúť, že vlastne vieme vyjadriť aj samotnú veľkosť uhla \(\beta\). To vieme spraviť veľa rôznymi spôsobmi, napríklad cez súčet uhlov \(ABC\) a \(BCD\). Dostaneme \(3\beta+90^\circ - \frac \beta 2=180^\circ\), z čoho vypočítame \(\beta=36^\circ\). Teraz už môžeme vyjadriť väčšinu uhlov číselne.
Keď tak spravíme, všimneme si, že pri danej bete platí \(90^\circ - \frac \beta 2=2\beta\), teda aj \(\left| \sphericalangle BAC \right |=\left| \sphericalangle ABC \right |=72^\circ\). Následne, trojuholník \(ABC\) je rovnoramenný, \(|AC|=|BC|=|CD|=y\). To nám dáva, že aj trojuholník \(ADC\) je rovnoramenný a \(\left| \sphericalangle ADC \right |=\left| \sphericalangle DAC \right |\).
Na zistenie veľkosti uhla \(BAC\) nám už iba stačí nájsť presnú veľkosť uhla \(DAC\) a to napríklad cez súčet vnútorných uhlov trojuholníka \(ACD\). Tým získame \(\left| \sphericalangle DAC \right |=54^\circ\). Potom \(\left| \sphericalangle BAC \right |=\left| \sphericalangle DAC \right |+\left| \sphericalangle CAB \right |=54^\circ+72^\circ=126^\circ\).
Komentár - všeobecnejší pokec: Ak by sme si do nakresleného obrázku označili viaceré prebytočné uhly, bolo by oveľa ťažšie všimnúť si podstatné veci. Preto sa pred začatím označovania uhlov oplatí zamyslieť, ktoré uhly sa pravdepodobne využijú. Tiež sa oplatí zamyslieť, od koľkých rôznych uhlov závisí náš obrázok. Pomenovať viac uhlov v obrázku väčšinou nie je potrebné.
Počas riešenia geometrických úloh sa často vieme dostať do stavu, keď sme vyjadrili všetky možné uhly pomocou rozumne zvolených uhlov (v našom prípade pomocou uhla \(\beta\)). V tomto bode si je potrebné buď všimnúť nejakú dodatočnú vlastnosť (v našom prípade \(\beta=36^\circ\)), alebo je potrebné uberať sa iným smerom.
Komentár - užitočný pohľadu na geometriu: Keď sme si počas dokazovania všimli, že ďalšie uhly iba pomocou uhla \(\beta\) vyjadriť nevieme, mohli sme získať ďalšie nadhľady pomocou konštrukčného pohľadu na úlohu. Môžeme si všimnúť, že pri vedomostiach o obrázku v danom čase, lichobežník \(ABCD\) možno narysovať len pomocou uhla \(\beta\) a dĺžky \(|CD|\) (škály obrázku); avšak nie všetky takto získané lichobežníky \(ABCD\) spĺňajú podmienky zo zadania. Teda nie všetky možné veľkosti uhla \(\beta\) sú prípustné. Preto má zmysel pokúsiť sa nájsť veľkosť uhla \(\beta\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.