Zadanie
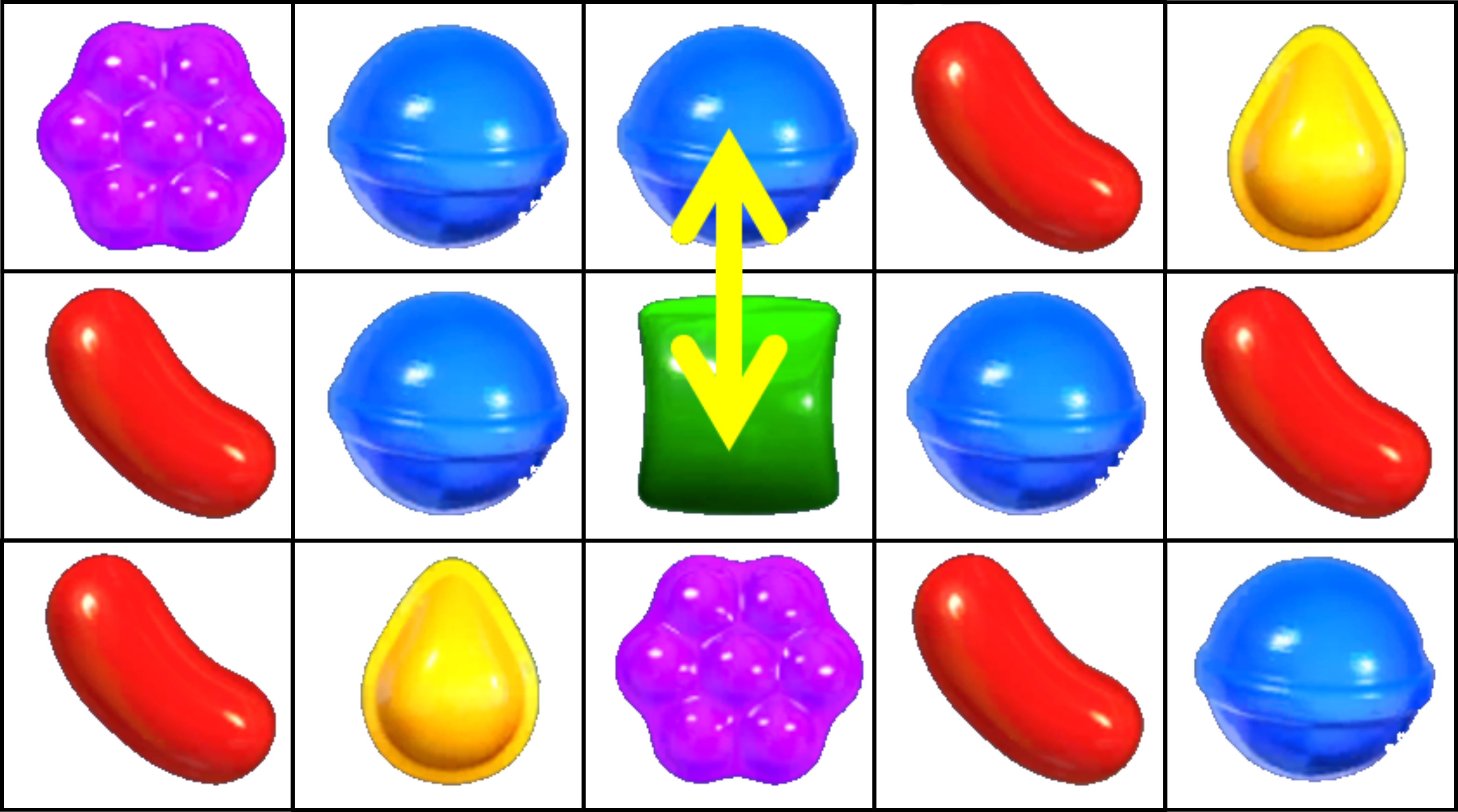
Keď prišiel Marcel aj so svojou sušičkou do FKSka, tak si všimol Mareka hrajúceho sa s cukríkmi1 nasledujúcu hru. Hra sa odohráva na pláne \(m \times n\) štvorcových políčok, kde \(m\), \(n\) sú celé čísla väčšie ako \(1\) a jedno z nich je aspoň \(3\). Na každom políčku sa nachádza cukrík práve jednej farby. V jednom ťahu môže Marek vymeniť cukríky na dvoch políčkach so spoločnou stranou, ale to len vtedy, ak sa po výmene budú vedľa seba nachádzať tri cukríky jednej farby v riadku alebo v stĺpci (ako na obrázku). Koľko najmenej farieb cukríkov potrebuje Marek na to, aby sa cukríky dali rozmiestniť do plánu tak, že:
v žiadnom riadku ani v žiadnom stĺpci sa nenachádzajú za sebou tri cukríky rovnakej farby,
nebolo možné spraviť žiaden ťah.
Výsledok určte v závislosti od čísel \(m\), \(n\).
Všetci vieme, že Marek s cukríkmi odmieta robiť čokoľvek iné ako sa s nimi hrať, napríklad ich jesť.↩
V zadaní úlohy nám vystupujú premenné \(m\) a \(n\). V takýchto prípadoch je dobré začať s nejakými malými hodnotami a zoznámiť sa tak s úlohou. Začnime teda s najmenšou možnou hodnotou \(m = 2\). Zo zadania vieme, že \(n\) musí byť aspoň \(3\). Už v tom najmenšom možnom pláne rozmerov \(2 \times 3\) máme tri políčka vedľa seba. Preto nám jedna farba cukríkov nestačí. Budú nám stačiť dve? Po chvíľke skúšania vieme zistiť, že áno.

Dokonca z toho môžeme odpozorovať, že podobným spôsobom vieme cukríky uložiť do ľubovoľného plánu s dvomi riadkami. Ak máme plán rozmerov \(2 \times n\) pre ľubovoľné prirodzené číslo \(n \ge 3\), tak ho vieme vyplniť dvomi cukríkmi nasledovne. Do každého druhého stĺpca počnúc prvým uložíme po dva červené cukríky a do zvyšných stĺpcov po dva žlté cukríky. Takto zaručíme, že v žiadnom riadku (a samozrejme aj stĺpci) nebudú tri cukríky rovnakej farby vedľa seba. Taktiež ľahko vidíme, že žiadnou výmenou nedostaneme tri rovnaké cukríky vedľa seba. Rovnaké argumenty platia aj pre plán rozmerov \(m \times 2\) – len celú situáciu otočíme o \(90^\circ\). Ukázali sme teda, že ak jeden z rozmerov plánu je \(2\), tak Marek potrebuje najmenej \(2\) farby cukríkov.

Poďme teda pokračovať a pozrime sa na väčšie plány. Ostali nám tie, v ktorých sú oba rozmery aspoň \(3\). Opäť si môžeme zobrať najmenší, teda plán rozmerov \(3 \times 3\). Pôjde vyplniť s dvomi farbami cukríkov? Nech sa snažíme, ako chceme, tak nám to nejde. Môžeme skúsiť teda tri cukríky, čo sa nám už vie podariť. Dokonca aj viacerými spôsobmi.
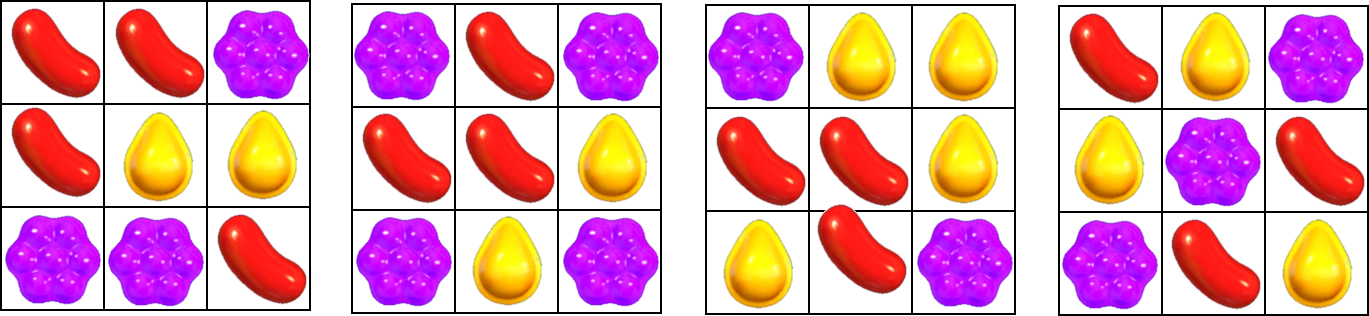
Takto si môžeme skúsiť vyplniť aj ďalšie malé rozmery plánov. Pokračujeme tak dovtedy, kým nezískame dostatočnú predstavu o úlohe. Ďalšie skúšanie už prenechávame na vás. Tu vo vzorovom riešení si vystačíme s tým, čo už máme. Môžeme tak odpozorovať, že Marekovi budú vždy stačiť tri farby cukríkov. Čo potrebujeme spraviť, aby sme sa v tom utvrdili?
Ukázať, ako plán správne vyplniť pomocou cukríkov troch farieb.
Zdôvodniť, prečo plán iba s dvomi farbami cukríkov vyplniť nevieme. (A tým pádom ho nevieme vyplniť ani menším počtom farieb.)
Vyplnenie tromi farbami cukríkov
Ako plán vyplníme? Úlohu máme vyriešiť všeobecne pre ľubovoľné rozmery plánu. Preto nemôžeme vypĺňať plán len tak hala-bala. Potrebujeme nájsť nejaký pekný systém. S tým môžeme začať už pri vypĺňaní plánu \(3 \times 3\). Posledné umiestnenie cukríkov vyzerá celkom sľubne. Napr. plán \(5 \times 11\) by sme podľa neho vedeli vyplniť takto:
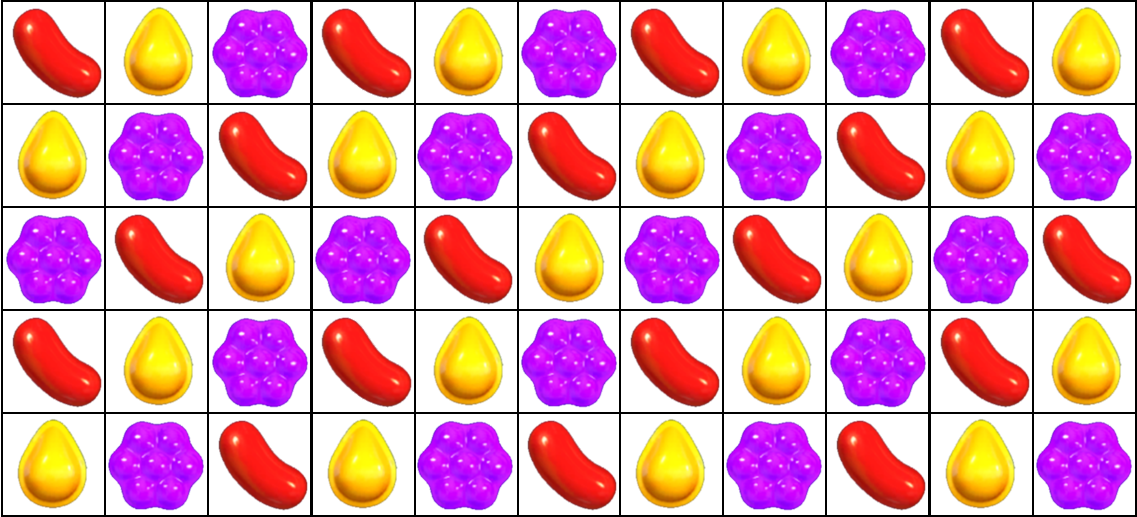
Poďme to napísať poriadne, všeobecne. Plán budeme vypĺňať po diagonálach, ktoré smerujú sprava hore smerom doľava nadol. Prvú diagonálu, teda jedno políčko v ľavom hornom rohu plánu, zaplníme červeným cukríkom. Do druhej diagonály umiestnime žlté cukríky. Do tretej diagonály fialové. Potom zas červené, žlté, fialové, … V tomto poradí postupne vypĺňame diagonály cukríkmi týchto farieb, až kým nevyplníme celú tabuľku.
Spĺňa takéto vyplnenie potrebné vlastnosti? V každom riadku a aj v každom stĺpci sa farby cukríkov striedajú. Preto nemáme ani v riadku, ani v stĺpci tri cukríky rovnakej farby za sebou. Môžeme spraviť nejaký ťah? Uvedomme si, že existujú len dva možné druhy ťahov. V jednom prípade máme v riadku alebo stĺpci dva cukríky rovnakej farby vedľa seba a výmenou k nim presunieme tretí. V druhom prípade máme dva cukríky rovnakej farby, medzi ktorými je jedno políčko a výmenou presunieme medzi dva rovnaké cukríky tretí. Avšak pri našom rozložení sú v každom riadku medzi cukríkmi rovnakých farieb dve políčka. Nemáme tam teda v žiadnom riadku ani dva rovnaké cukríky vedľa seba, ani ob jedno políčko. Preto nevieme spraviť žiaden ťah. Tým pádom je naše rozmiestnenie cukríkov korektné.
Prečo menej nestačí?
A dve farby Marekovi stačiť nebudú? Pozrime sa, ako by to vyzeralo, kebyže Marek má len dve farby cukríkov. Oba rozmery plánu sú aspoň \(3\). Preto vieme v pláne nájsť štvorec \(3 \times 3\) políčka, trebárs ten v ľavom hornom rohu. Stačí nám ukázať, že už len tento štvorec Marek nevie vyplniť. Potom totiž nebude vedieť vyplniť celý plán. A to je dobrá správa. Štvorec \(3 \times 3\) políčka je celkom malý a môžeme v ňom prebrať všetky možnosti, ako môže Marek umiestňovať cukríky. Na to je dobré si nájsť nejaký systém. V závislosti od neho môžeme preberať viac alebo menej prípadov. My si ukážeme jeden z tých stručnejších prístupov.
Pozrime sa na druhý stĺpec nášho štvorca \(3 \times 3\). Keďže sú v ňom tri políčka, tak tam musíme mať dva cukríky rovnakej farby. Kľudne si môžeme povedať, že je to žltá farba. Zvyšný cukrík v druhom riadku musí byť druhej farby, povedzme červenej. Riadok, v ktorom sa nachádza tento červený cukrík, si nazveme smutný. Môže byť na niektorom políčku smutného riadku žltý cukrík? Na prvom políčku smutného riadku nemôže byť. Ak by tam bol, tak by sme mohli spraviť platný ťah vymenením prvých dvoch políčok smutného riadku. Z rovnakého dôvodu nemôžeme mať žltý cukrík ani na treťom políčku smutného riadku. Teda na všetkých políčkach smutného riadku musí byť červený cukrík. To sa ale nemôže stať. Smutný riadok je teda naozaj smutný, lebo kvôli nemu Marek nemôže vyplniť štvorec \(3 \times 3\) iba dvomi farbami cukríkov. A teda Marek tak nevie vyplniť ani celý plán, pokiaľ má oba rozmery aspoň \(3\).

Záver
Týmto je naša úloha hotová. Ukázali sme teda, že najmenší počet farieb cukríkov, ktorý Marek potrebuje je:
\(2\), pokiaľ \(m = 2\) alebo \(n = 2\);
\(3\), pokiaľ \(m \ge 3\) a zároveň \(n \ge 3\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.