Zadanie
Po pár dňoch tajného používania sa sušička v KMSku pokazila. Miro si povedal: „Ízy“ a dal sa do jej opravovania. Keďže nie je žiaden amatér, spraví to bez návodu. Celú ju rozobral na súčiastky, a potom zložil zase naspäť. Jedna súčiastka mu však ostala na stole a ani za nič si nevedel spomenúť kam patrí. Patrila konkrétne do bodu \(D\). Ukážte Mirovi, že bod \(D\) patrí do stredu úsečky \(AE\).
Je daný trojuholník \(ABC\). Nech \(k_1\) je kružnica, ktorá prechádza bodom \(B\) a dotýka sa priamky \(AC\) v bode \(A\). Nech \(k_2\) je kružnica, ktorá prechádza bodom \(C\) a dotýka sa priamky \(AB\) v bode \(A\). Označme \(D\) priesečník kružníc \(k_1\) a \(k_2\) rôzny od \(A\). Priamka \(AD\) pretína kružnicu opísanú trojuholníku \(ABC\) v bode \(E\) rôznom od \(A\). Dokážte, že \(D\) je stredom úsečky \(AE\).
Označíme si vnútorné uhly trojuholníka \(ABC\) štandardne \(\alpha, \beta, \gamma\). Ďalej si označíme \(O\) stred kružnice opísanej trojuholníku \(ABC\), \(O_1\) a \(O_2\) stredy kružníc \(k_1\) a \(k_2\). Budeme uvažovať konfiguráciu, kde \(A\) je v tej istej polrovine ako bod \(C\) danej osou strany \(BC\).
Ako prvé si riešiteľ môže všimnúť niekoľko vlastností. Veľa z nich nie je podstatných, pre toto konkrétne riešenie no nevylučujeme možnosť, že môžu viesť na riešenie. Ako to už zvykom býva pri riešení geometrie, budeme sa venovať iba tým vlastnostiam, ktoré vedú k riešeniu a ostatné naozaj zaujímavé postrehy necháme na riešiteľa, aby ich našiel a možno z nich vyčaroval riešenie (alebo sa z nich aspoň tešil).
Zo stredového, obvodového a úsekového uhla je po zamyslení zrejmé, že \(|\sphericalangle AO_2C|=2\alpha\). (Zamyslenie znamená, zoberme ľubovoľný bod \(X\) na oblúku \(k_2\) neobsahujúci \(D\), trojuholník \(AXC\) má obvodový uhol pri \(X\), ktorý má zhodnú veľkosť ako úsekový uhol \(|\sphericalangle BAC|=\alpha\), stredový je teda dvojnásobok.) Obdobne \(|\sphericalangle BO_1A| = 2\alpha\). Následne znovu zo stredového a obvodového uhla vidíme, že \(|\sphericalangle CDA|= 180^\circ - \alpha\) a \(|\sphericalangle ADB| = 180^\circ - \alpha\). Preto \(|\sphericalangle EDC|=\alpha\), aj \(|\sphericalangle BDE|=\alpha\).
Na to, aby sme ukázali, že \(D\) je stredom úsečky, treba ukázať, že \(DO\) je kolmica na \(AE\) (t. j. kolmica na tetivu idúca stredom kružnice polí tetivu).
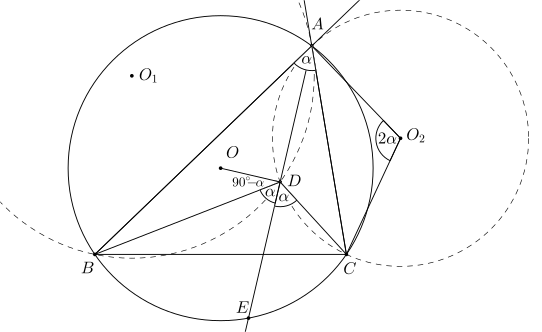
Teraz si všimnime, že \(|\sphericalangle BDC|=2\alpha=|\sphericalangle BOC|\), teda \(BODC\) ležia na kružnici v tomto poradí (vzhľadom na našu konfiguráciu). Ďalej \(|\sphericalangle OCB|=90^\circ-\alpha\), nakoľko \(OCB\) je rovnoramenný trojuholník a uhol \(|\sphericalangle BOC|=2\alpha\). Taktiež vďaka tetivovosti \(BODC\) vieme teraz, že aj \(|\sphericalangle ODB|=90^\circ-\alpha\). A teda v súčte s \(|\sphericalangle BDE|\) máme veľkosť uhla \(|\sphericalangle ODE|=90^\circ\). Preto \(D\) je stredom úsečky \(AE\).
Autorova poznámka: Prezentované riešenie je výrazne jednoduchšie a úhľadnejšie ako autor pôvodne úlohu vyriešil. Samotné vyriešenie úlohy je len polovicou roboty, druhou polovicou (možno ľahšou) je napísať riešenie tak, aby neobsahovalo plevel a stále bolo matematicky správne. Preto sa treba zamyslieť pri spisovaní riešenia, čo skutočne potrebujeme, čo bude prekážať a čomu sa nakoniec môžeme vyhnúť úplne. Autor sa takto napríklad vyhol zbytočnému označeniu uhlov \(\delta= |\sphericalangle DBO|\), \(\epsilon = |\sphericalangle OBA|\), ktoré v odplevelovanom riešení nie sú nakoniec potrebné.
Bonusová myšlienka: Môžeme si všimnúť, že stredy strán \(AB\) a \(AC\) a body \(D\), \(O\), \(A\) ležia na Tálesovej kružnici nad priemerom \(AO\). Ak by sa nám podarilo dokázať túto vlastnosť skorej ako kolmosť uhla \(ODE\), tak kolmosť máme zadarmo, a teda aj úlohu.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.