9. Koeficient, Majo a Sušička vzorové riešenie

Chceli by sme, aby ľavá strana nerovnosti bola čo najmenšia, zatiaľ čo tá pravá čo najväčšia, pretože tak dosiahneme čo najväčšie obmedzenie na \(k\). Chceli by sme teda nájsť také trojuholníky, pre ktoré je \(12a^2+b^2+c^2\) čo najmenšie, zatiaľ čo \(S\) je čo najväčšie. Trojuholníkov existuje nesmierne veľa, bolo by teda dobré nejakým spôsobom sa obmedziť na tie, ktoré čo najviac minimalizujú ľavú stranu nerovnosti a maximalizujú obsah trojuholníka.

Ukážeme, že zaujímavé sú práve rovnoramenné trojuholníky s \(b=c\). Ak sa pozrieme na všetky trojuholníky pre konkrétne \(a\) a \(S\), máme pevne danú aj ich výšku na stranu \(a\), ktorá sa dá vypočítať zo vzťahu

\[\begin{aligned} S=\frac{av_a}{2}.\end{aligned}\]

Ďalej budeme používať len výšku na stranu \(a\), takže ju budeme značiť už iba \(v\). Keď máme takto zafixované \(a\) a \(S\), ostáva už len minimalizovať \(b^2+c^2\). Oba sčítance vieme vypočítať z Pytagorovej vety.

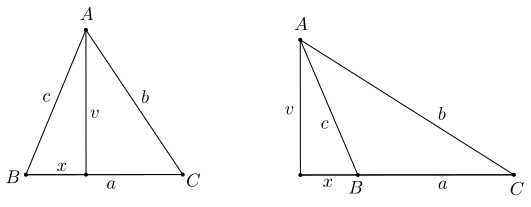
Nech \(x\) označuje vzdialenosť päty výšky na stranu \(a\) od jej krajného bodu \(B\). Ak päta leží vnútri strany \(a\) alebo je zhodná s niektorým krajným bodom, z Pytagorovej vety platí:

\[\begin{aligned} b^2 &= (a-x)^2 + v^2,\\ c^2 &= x^2 + v^2.\end{aligned}\]

Ak päta neleží vnútri strany \(a\), nech BUNV¹ leží na polpriamke opačnej k \(BC\) (ak máme \(BC\) vodorovne smerom doprava, tak leží naľavo od \(B\)). Prípad, kedy leží napravo od \(C\) je symetrický. Potom opäť použijeme Pytagorovu vetu a máme

\[\begin{aligned} b^2 &= (a+x)^2 + v^2,\\ c^2 &= x^2 + v^2.\end{aligned}\]

Vidíme, že sme si vôbec nepomohli, práve naopak. Hodnota \(b^2\) sa zväčšila, namiesto \((a-x)^2\) máme v súčte \((a+x)^2\). Hodnota \(c^2\) sa nezmenila. Keďže chceme \(b^2+c^2\) minimalizovať, tento prípad nebudeme ďalej uvažovať.

Ak je trojuholník rovnoramenný, potom \(b^2 = c^2 = v^2 + (\frac{a}{2})^2\). Chceme dokázať, že v tomto prípade je \(b^2 + c^2\) najmenšie možné, teda:

\[\begin{aligned} ((a-x)^2 + v^2) + (x^2 + v^2) &\geq 2\left(v^2 + \left(\frac{a}{2}\right)^2\right),\\ a^2 - 2ax + 2x^2 + 2v^2 &\geq 2v^2 + \frac{a^2}{2}.\end{aligned}\]

Prenásobíme dvomi:

\[\begin{aligned} a^2 - 4ax + 4x^2 &\geq 0,\\ (a-2x)^2 &\geq 0.\end{aligned}\]

Druhá mocnina vždy bude nezáporná a postupovali sme ekvivalentnými úpravami, takže toto tvrdenie je dokázané. Navyše pre iné \(x\) ako \(\frac{a}{2}\) rovnosť nenastáva. Stačí uvažovať rovnoramenné trojuholníky. Vyjadrenie \(b\), \(c\) a \(S\) pomocou \(a\) a \(v\) teraz dosadíme do pôvodnej nerovnosti a opäť prenásobíme dvomi:

\[\begin{aligned} 12a^2 + 2v^2 + \frac{a^2}{2} &\geq k \frac{av}{2},\\ 25a^2 + 4v^2 &\geq kav,\\ 25a^2 - kav + 4v^2 &\geq 0.\end{aligned}\]

Toto nám nápadne pripomína roznásobenie druhej mocniny rozdielu, konkrétne

\[\begin{aligned} (5a-2v)^2 = 25a^2 - 20av + 4v^2.\end{aligned}\]

Vidíme, že ak zvolíme \(k=20\), dostaneme opäť druhú mocninu, ktorá má byť väčšia alebo rovná nule, nerovnosť je splnená. Ak by však \(k\) bolo väčšie ako \(20\), mali by sme

\[\begin{aligned} 25a^2 - kav + 4v^2 = (5a-2v)^2 + 20av - kav = (5a-2v)^2 + av(20 - k)\geq 0,\end{aligned}\]

čo už platiť nemusí, stačí ak \((5a-2v)^2\) bude \(0\) a \(av\) kladné.

Hľadané \(k\) je teda \(20\). Rovnosť nastáva vtedy, kedy nastáva v uvedených nerovnostiach, teda \(5a=2v\) a \(b=c\), čiže

\[\begin{aligned} b^2 = c^2 = v^2 + \left(\frac{a}{2}\right)^2 = \left(\frac{5a}{2}\right)^2 + \left(\frac{a}{2}\right)^2 = \frac{26a^2}{4}.\end{aligned}\]

Z toho vyplýva

\[\begin{aligned} b = c = \sqrt{\frac{13}{2}}a.\end{aligned}\]

Pre všetky takéto trojuholníky v zadanej nerovnosti pre \(k=20\) nastáva rovnosť.