Zadanie
Na rozdiel od Sparty Aténski predstavitelia dbali na to, aby ich bojovníci – hopliti, mali nielen krásne vyšportované telá, ale aj bystrú a rozhľadenú myseľ. Tento ideál súladu fyzickej a duševnej krásy, nazývaný tiež Kalokagatia, bol pre Aténsku spoločnosť nesmierne dôležitý. Aj preto dávali svojim vojakom pred jedlom vždy nejakú mentálnu rozcvičku, ktorú museli vyriešiť, aby sa mohli dosýta najesť. Jedlo si museli zaslúžiť. Z dobových rytín a malieb na urnách sa nám dochoval tento príbeh:
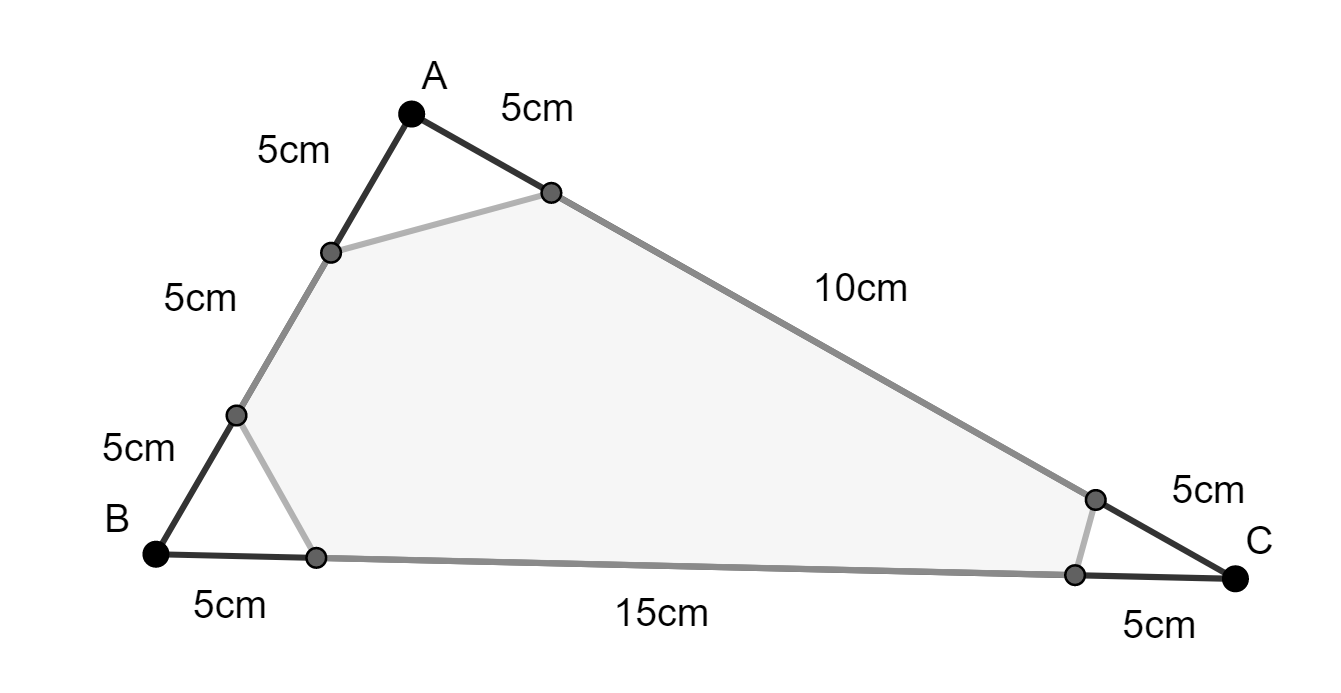
Múdry generál Perikles raz prišiel za svojimi vojakmi, ktorí práve obedovali fazuľu s tradičným gréckym nekysnutým chlebom – pitou, ktorý bol v tvare trojuholníka so stranami dĺžok \(15\), \(20\) a \(25\) cm ako na obrázku. Skôr, ako sa vojak stihol do pity pustiť, prišiel za ním Perikles a ostrým nožom mu odrezal z každého rohu kúsok v tvare rovnoramenného trojuholníka s dĺžkou ramien \(5\) cm a povedal vojakovi: „Ak by si chcel tieto kúsky zjesť, drahý spolubojovník, budeš mi musieť najprv povedať, koľko z pity ti ostalo. Odpovieš mi však nesprávne, hodím celú pitu mačkám, ktoré už nervózne žobrú pod tvojimi nohami.“
Skúste sa teraz aj vy zamyslieť nad danou úlohou a zistite obsah plochy, ktorá vojakovi ostala. Podarí sa vám to alebo vašu porciu hodia mačkám?
Zo zadania aj z obrázku vidíme, že obsah zostávajúcej plochy – šesťuholníka \(A_CA_BB_AB_CC_BC_A\) zistíme tým, že od pôvodného trojuholníka \(ABC\) odčítame obsahy malých (odrezaných) trojuholníkov. Ako jedna z prvých vecí, čo nám môže napadnúť skúsiť, keďže poznáme dĺžky všetkých strán trojuholníka \(ABC\), je vhodne ich dosadiť do Pytagorovej vety. Ak by platila, vedeli by sme, že trojuholník je pravouhlý. Tak to spravme. Po dosadení sme prišli na to, že trojuholník \(ABC\) je pravouhlý s pravým uhlom pri vrchole \(A\), pretože \(15^2+20^2=25^2\).
Keď už vieme, že trojuholník \(ABC\) je pravouhlý, jeho obsah zistíme ľahko. Dĺžky jeho strán \(AB\) a \(AC\) dosadíme do vzorca na obsah trojuholníka a zistíme, že \(T=\frac{1}{2} \cdot |AB|\cdot|AC|= \frac{1}{2} \cdot 15 \cdot 20=150\ \text{cm}^2\). Veľkosť malého trojuholníka pri pravom uhle zistíme podobne. Použijeme jeho dĺžky strán a dostávame \(T_1=\frac{1}{2} \cdot |AA_B| \cdot |AA_C| = \frac{1}{2} \cdot 5 \cdot 5= 12.5\ \text{cm}^2\). Náročnejšie bude zistiť obsahy zvyšných dvoch trojuholníkov.
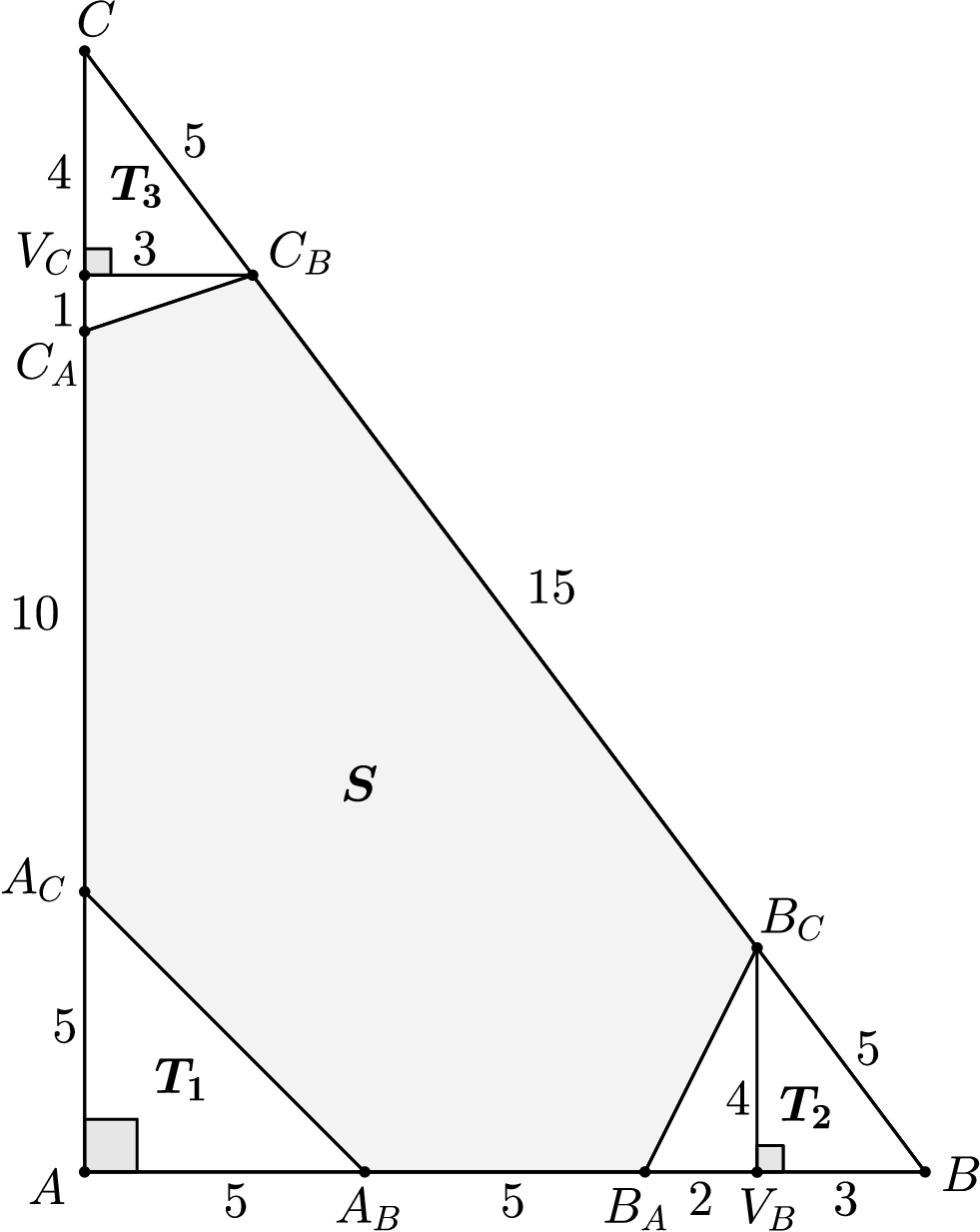
Pri výpočte obsahu malého trojuholníka \(BB_AB_C\) si pomôžeme veľkým trojuholníkom \(ABC\). Ak by sa nám podarilo ukázať, že nejaká časť tohto trojuholníka je podobná s trojuholníkom \(ABC\), mohli by sme pomocou koeficientu podobnosti určiť dĺžky strán tejto časti trojuholníka \(BB_AB_C\). Ak to spravíme šikovne, z tohto poznatku by sme potom mohli vedieť vypočítať aj obsah celého trojuholníka \(BB_AB_C\). Pomôžeme si tým, že budeme viesť výšku z vrchola \(B_C\) na stranu \(BB_A\), čím zároveň rozdelíme trojuholník \(BB_AB_C\) na dva menšie trojuholníky. Pätu tejto výšky si nazveme \(V_B\). Vieme, že uhol pri päte výšky \(V_B\) je pravý. Môžeme si všimnúť, že oba trojuholníky \(ABC\) a \(V_BBB_C\) sú pravouhlé a majú spoločný uhol pri vrchole \(B\). Potom podľa vety \(uu\) o podobnosti trojuholníkov vieme, že trojuholníky \(ABC\) a \(V_BBB_C\) sú (v tomto poradí) podobné. Koeficient podobnosti \(k\) je pomer dĺžok strán \(BB_C\) a \(BC\). Teda \[k = \frac{|BB_C|}{|BC|} = \frac{5}{25} = \frac{1}{5}.\]
Pomocou koeficientu podobnosti \(k\) zistíme dĺžku výšky \(|B_CV_B| = k \cdot|AC| = \frac{1}{5} \cdot 20=4\) cm. Keďže poznáme dĺžku strany \(BB_A\) a dĺžku výšky na danú stranu, vieme ľahko dopočítať obsah trojuholníka \(BB_AB_C\). Teda \[T_2=\frac{|BB_A| \cdot |B_CV_B|}{2} =\frac{5 \cdot 4}{2} = 10\ \text{cm}^2.\]
Pri výpočte obsahu posledného odrezaného trojuholníka budeme postupovať rovnako ako pri predchádzajúcom trojuholníku. Trojuholník \(CC_AC_B\) si môžeme výškou na stranu \(CC_A\) rozdeliť na dva menšie trojuholníky. Podľa vety \(uu\) o podobnosti trojuholníkov sú trojuholníky \(ABC\) a \(V_CC_BC\) podobné. Môžeme si všimnúť, že ich koeficient podobnosti je \[k' = \frac{|CC_B|}{|CB|} = \frac{5}{25} = \frac{1}{5}.\]
Potom výška \(V_CC_B\) je podobná so stranou \(AB\) a má veľkosť \(3\ \text{cm}\). Keď už poznáme aj dĺžku výšky v trojuholníku \(|CC_AC_B|\), ľahko dopočítame jeho obsah \[T_3~=~\frac{|CC_A| \cdot |C_BV_C|}{2}~=~\frac{5 \cdot 3}{2}~=~7.5\ \text{cm}^2.\]
Na záver nám už len ostáva od veľkosti obsahu trojuholníka \(ABC\) odrátať obsahy trojuholníkov \(AA_BA_C\), \(BB_AB_C\) a \(CC_AC_B\). Výsledkom je obsah zostávajúcej plochy \(S = T - T_1 - T_2 - T_3 = 150 - 12.5 - 10 - 7.5 = 120\ \text{cm}^2\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.