5. Korporácii Modeluj Symbol vzorové riešenie

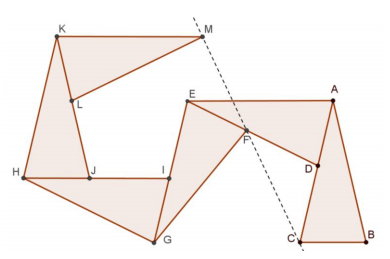
Akým spôsobom by sme vedeli dokázať, že body \(M, F, C\) ležia na jednej priamke? Predsa pomocou vrcholových uhlov, stačí dokázať \(|\sphericalangle CFD|=|\sphericalangle EFM|\). Keďže zadané trojuholníky sú zhodné a rovnoramenné, tvar celého obrázka závisí len od jedného uhla. Napríklad keď si označíme \(|\sphericalangle ACB|=\alpha\), všetky ostatné uhly závisia len od hodnoty \(\alpha\) a pri troche šťastia by sa nám ich mohlo podariť dopočítať. Každý z našich šesť zhodných trojuholníkov má dva uhly rovné \(\alpha\) a jeden uhol \(180^\circ-2\alpha\).

Vyjasnime si ešte jednu vec. Zadanie hovorí, že trojuholníky sú umiestnené ako na obrázku, čím sa myslí aj to, že body sú usporiadané v rovnakom poradí ako na obrázku. To konkrétne znamená, že bod \(D\) leží vnútri úsečky \(AC\), čo je to ekvivalentné s tým, že trojuholník \(ABC\) má kratšiu základňu ako ramená, \(|CB|<|AC|\).

Zamerajme sa na uhol \(|\sphericalangle CFD|\). Trojuholník \(CDF\) je rovnoramenný, lebo \(|FD|=|ED|-|EF|=|AC|-|AD|=|CD|\). Vieme, že uhol \(FDA\) má veľkosť \(\alpha\) a je vonkajším uhlom v trojuholníku \(CDF\). Využijeme, že súčet dvoch vnútorných uhlov trojuholníka je rovný vonkajšiemu protiľahlému uhlu (premyslite si), teda \(|\sphericalangle CFD|+|\sphericalangle FCD|=|\sphericalangle FDA|=\alpha\). Zároveň z rovnoramennosti sú uhly \(|\sphericalangle CFD|\) a \(|\sphericalangle FCD|\) rovnaké, takže oba majú veľkosť \(\alpha /2\).

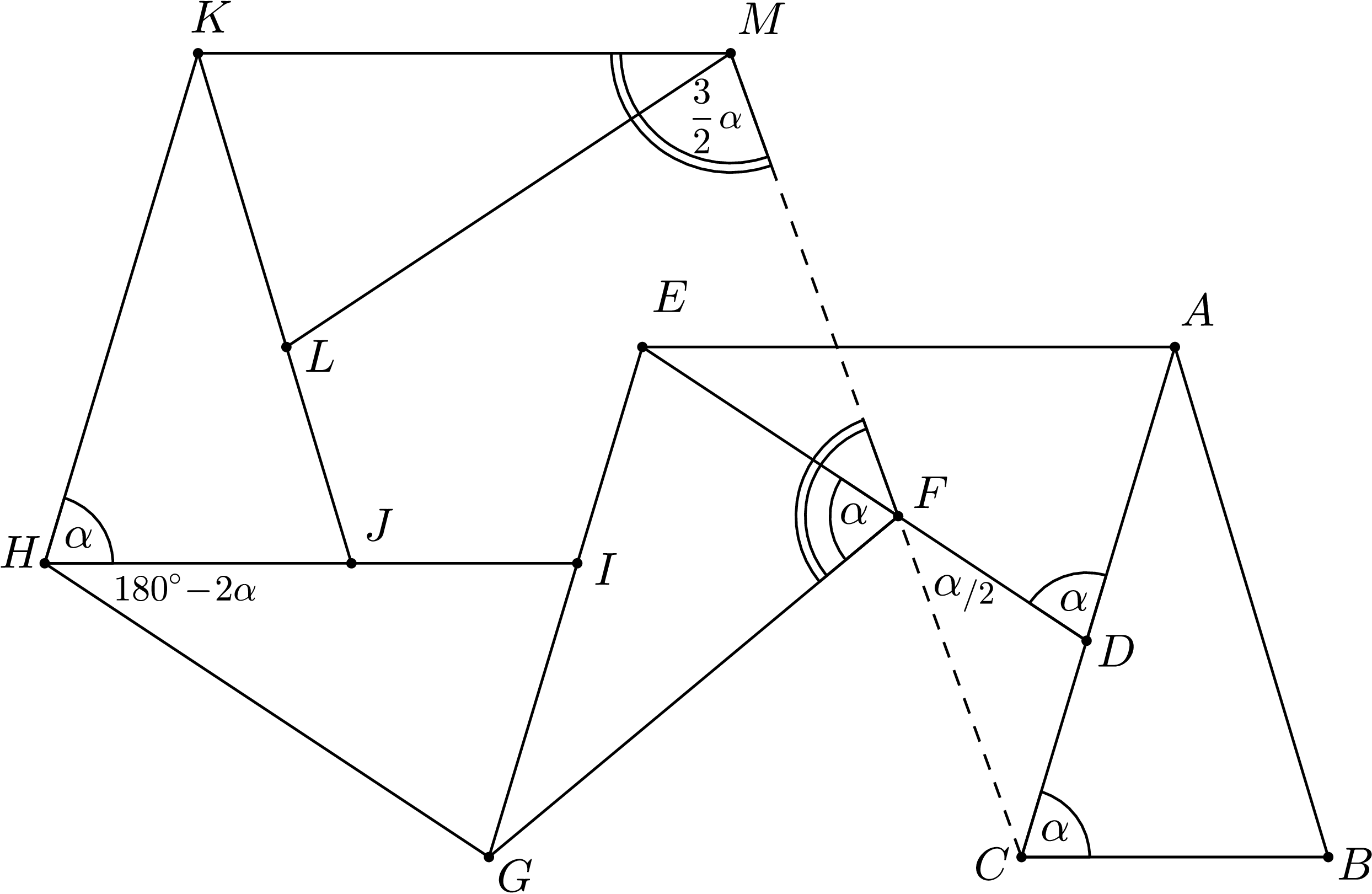
Teraz by sme chceli vyjadriť uhol \(|\sphericalangle EFM|\), ideálne aby bol tiež \(\alpha /2\). Všimnime si päťuholník \(FGHKM\). Štyri jeho strany majú rovnakú dĺžku a tri uhly \(FGH\), \(GHK\), \(HKM\) majú rovnakú veľkosť, lebo sú zložené z dvoch uhlov \(\alpha=|\sphericalangle IGH|=|\sphericalangle JHK|=|\sphericalangle LKM|\) a \(180^\circ-2\alpha=|\sphericalangle FGE|= |\sphericalangle GHI|=|\sphericalangle HKJ|\). Päťuholník vyzerá byť symetrický podľa osi úsečky \(MF\). Dalo by sa to zdôvodniť tým, že rovnoramenný trojuholník \(GHK\) je symetrický podľa osi uhla \(GHK\), na úsečky \(HK\) a \(HG\) napojíme úsečky \(KM\) a \(GF\) rovnakej dĺžky pod rovnakými uhlami, takže budú tiež symetrické podľa tejto osi uhla. Potom obraz uhla \(KMF\) v osovej súmernosti podľa tejto osi je uhol \(GFM\), takže majú rovnakú veľkosť: \(|\sphericalangle KMF|=|\sphericalangle GFM|\).

Uvedieme ešte jedno zdôvodnenie rovnosti \(|\sphericalangle KMF|=|\sphericalangle GFM|\). Rovnoramenné trojuholníky \(FGH\) a \(HKM\) sú zhodné podľa vety \(sus\), takže \(|HF|=|HM|\). Trojuholník \(MHF\) je rovnoramenný, takže \(|\sphericalangle HFM|=|\sphericalangle HMF|\). Už ľahko spočítame rovnosť uhlov \(|\sphericalangle KMF|=|\sphericalangle KMH|+|\sphericalangle HMF|=|\sphericalangle GFH|+|\sphericalangle HFM|=|\sphericalangle GFM|\).

Ďalej použijeme poznatky, že \(|\sphericalangle KMF|=|\sphericalangle GFM|\), a že súčet uhlov v päťuholníku je \(540^\circ\) a dostaneme \[|\sphericalangle GFM|=\frac{540^\circ-3|\sphericalangle GHK|}{2}=\frac{540^\circ-3(180^\circ-\alpha)}{2}=\frac{3\alpha}{2}.\]

Nakoniec naozaj dostávame \(|\sphericalangle EFM|=|\sphericalangle GFM|-|\sphericalangle GFE|=\frac{3}{2}\alpha-\alpha=\alpha/2\), čím sme dokázali, že body \(M, F, C\) budú vždy ležať na jednej priamke, nezávisle od tvaru trojuholníka \(ABC\).