Zadanie
„Ser Pepper!“ kričal zadychčaný muž texaským dialektom, „Komančovia sa vrátili! V noci1 do našich úrodných polí doniesli obrovskú stenu, a do nej vypálili znak. Musíte nám pomôcť.“ Sgt. Pepper neváhal. Povedal jeho povestné „Idem, riešim,“ nasadol na koňa a vybral sa za kovbojom. Až dorazili na miesto činu a prisvietili si svojimi fakľami, odkryl sa im takýto obraz:
Nech \(ABCD\) je tetivový štvoruholník, pre ktorý platí \(|DA| < |AB| = |BC| < |CD|\). Body \(E\) a \(F\) sú postupne zvolené na stranách \(CD\) a \(AB\) tak, že priamky \(BE\) a \(AC\) sú na seba kolmé a priamky \(EF\) a \(BC\) sú rovnobežné. Dokážte, že \(|FB| = |FD|\).
Čiže teraz, lebo teraz bola noc.↩︎
Napriek tomu, že úloha bola zaradená ako ôsma, jej riešenie si vyžaduje iba tie najzákladnejšie vedomosti a ich aplikácia je relatívne priamočiara. Dalo by sa povedať, že na vyriešenie tejto úlohy je potrebné „čisté uhlenie“. Ak ste túto úlohu nevyriešili, odporúčam vám venovať tomuto vzoráku plnú pozornosť a snažiť sa odniesť si čo najviac princípov.
Najpriamočiarejší spôsob, ako ukázať, že dĺžky dvoch úsečiek stretávajúcich sa v jednom bode sú rovnaké, je jednoducho ukázať, že trojuholník vytvorený týmito dvomi úsečkami je rovnoramenný. Naším cieľom je ukázať rovnoramennosť trojuholníka \(BDF\). Najjednoduchšie sa to dá tak, že ukážeme rovnosť \(|\sphericalangle{BDF}|=|\sphericalangle{DBF}|\). Uhol \({DBF}\) je vďaka vete o obvodových uhloch rovný uhlu \({ACE}\). Priamo zo zadania tiež máme rovnosť uhlov \({BAC}\) a \({BCA}\) a opäť, použitím vety o obvodových uhloch tiež \({BDC}\).
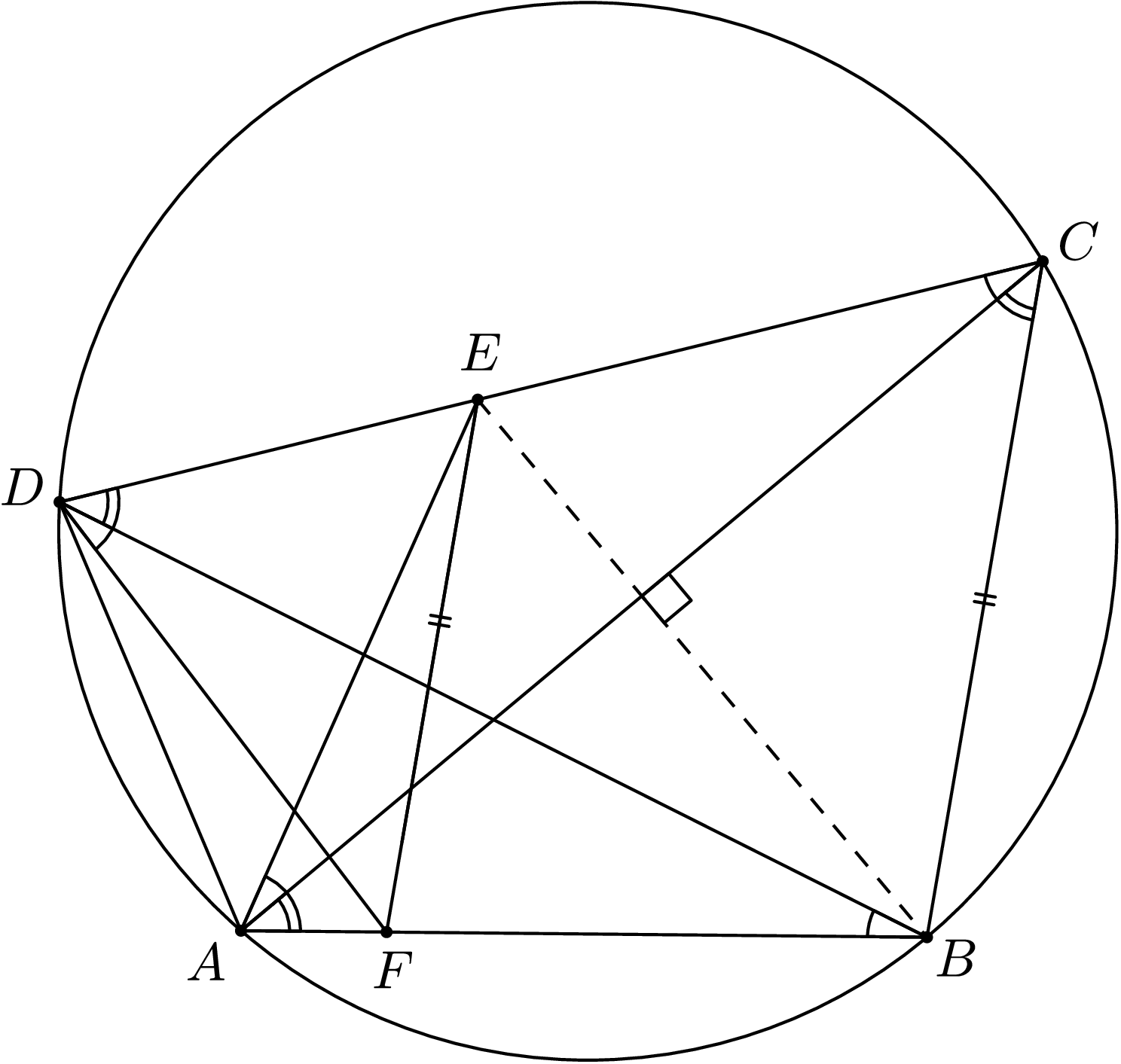
Teraz už budeme musieť trochu pohútať. Šikovné geometrické oko si hneď všimne, že nakoľko strana \(EF\) je rovnobežná so stranou \(BC\), musí byť štvoruholník \(AFED\) tetivový. To vidno napríklad tak, že uhol \({FED}\) je rovnako veľký ako \({BCD}\) (z rovnobežnosti), a teda je rovný \(180^\circ-|\sphericalangle{FAD}|\), z čoho už tetivovosť, podľa známeho a dôležitého tvrdenia o protiľahlých uhloch v tetivovom štvoruholníku, vyplýva.
To nás motivuje dokresliť aj stranu \(AE\), aby sme mohli plne využívať obvodové uhly aj v štvoruholníku \(AFED\). Teraz vieme preniesť náš dôležitý uhol \({FDB}\) na uhol \({CAE}\). Toto nevyplýva priamo použitím obvodových uhlov, ale až dopočítaním z rovnosti uhlov \({FDE}\) a \({FAE}\) po odpočítaní identických uhlov \({BAC}\) a \({BDC}\).
Vidíme, že ak majú byť rovnaké uhly \({FDB}\) a \({FBD}\), potom sme práve vyuhlili, že aj uhly \({CAE}\) a \({ACE}\) by boli rovnaké (a naopak, z rovnakosti týchto dvoch uhlov spätne vyplýva aj rovnakosť našich pôvodných). Teda trojuholník \(ACE\) musí byť rovnoramenný. Teda \(E\) musí ležať na osi strany \(AC\). Ale keďže priamka \(BE\) bola definovaná ako kolmica z \(B\) na \(AC\) a \(ABC\) je rovnoramenný trojuholník, \(BE\) musí byť os strany \(AC\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.