Zadanie
Kráľ schmatol meč a vyhrnul sa von z dverí. Krutitruľo sa obrátil a zakričal na mňa: „Pozri, tam je napísané: „Tajná chodba do Srdca Abstrakcie“!“ Žiaľ, viac povedať nemohol, lebo vojaci v miestnosti sa zabstrahovali na Lieove grupy a jeden za druhým si naňho políhali, až z neho ostal len mastný fľak. „Za ním!“ zakričal za mnou niekto a mne nebolo treba dva razy hovoriť. Vkĺzol som do dverí, na ktoré ukazoval Krutitruľo, a uháňal som krútiacou sa chodbičkou. Pod mojimi nohami sa otriasali rovnice tuhosti, pri každej zákrute sa sušili nepotrebné dimenzie, ako zábradlia mi slúžili geometricky dokonalé rovnobežky. Konečne som vybehol spoza rohu a ocitol som sa v čudesnej miestnosti s nekonečným povrchom, no len asi dvadsiatimi kubíkmi objemu. Uprostred na podstavci sálalo bledomodré svetlo z obrovského diamantu. Počul som za sebou v diaľke kroky, tak som rýchlo zašmátral po Konkretizátore – a nahmatal som len vzduch. Niekde mi musel vypadnúť z vrecka. Oblial ma pot. Čo teraz? Kroky sa blížili. Prizrel som sa Srdcu lepšie. Bolo nádherné. Jeho povrch sa víril a zakrúcal v slabučkých vzduchových prúdoch, takže vyzeralo, akoby bolo vytesané z dymu. Jeho žiara nebola centralizovaná, ale pochádzala z miliárd malilinkých bodiek... Naklonil som sa bližšie. Galaxie sa mi pred očami krútili, uprostred každej čierna diera. Obzrel som sa po komôrke. Po stenách boli namaľované všemožné fyzikálne a matematické zákony. Všetky smerovali k Srdcu. Komôrka nebola tvarovaná Srdcom – Srdce bolo tvarované komôrkou, a všetkým ostatným v Abstrakcii takisto. Kroky boli pár metrov za mnou. Vykročil som do Srdca. Jedna z jeho galaxií sa volá Mliečna cesta. Tam niekde je môj domov.
Ale ešte predtým som prehodil zopár znamienok, aby Fermatova veta v našom vesmíre platila. A nechal som vo fabrike časopriestoru vpísanú jednu úlohu, len pre vás:
Máme trojuholník \(ABC\), v ktorom \(|AC|\neq |BC|\). Kružnica jemu vpísaná má stred v bode \(I\) a dotýka sa strán \(BC\), \(CA\), \(AB\) postupne v bodoch \(D\), \(E\), \(F\). Stred strany \(AB\) je \(M\). Kolmica z bodu \(I\) na ťažnicu \(CM\) sa pretína s priamkou \(DE\) v bode \(K\). Dokážte, že \(CK\) a \(AB\) sú rovnobežné.
Tento príklad sa dá vyriešiť pomerne jednoducho, ak poznáme a vieme pracovať s fenoménom zvaným harmonický štvorpomer. Ide o súhrn vlastností a tvrdení, ktorý sa často dá veľmi elegatne a efektívne využívať v geometrických úlohách, najmä na vyšších olympiádnych leveloch. Ak ste ešte nikdy o štvorpomere nepočuli, alebo by ste sa v ňom chceli zdokonaliť, či chytiť prax, odporúčam pozrieť 1 a 2.
Predtým, než túto úlohu ušľaháme týmto kladivom si harmonický štvorpomer zadefinujeme a uvedieme si tri tvrdenia z teórie harmonického štvorpomeru, ktoré pri tejto úlohe využijeme.
Definícia: Majme body \(A, C, B, D\) v tomto poradí na nejakej priamke. Hovoríme, že body \(A, C, B, D\) sú v harmonickom štvorpomere, ak platí \(\frac{|AC|}{|BC|}=\frac{|AD|}{|BD|}\). Navyše, majme bod \(P\) a body \(A, C, B, D\) tak, že tieto štyri body ležia na priamke v danom poradí a bod \(P\) leží mimo tejto priamky. Uvažujme priamky \(PA\), \(PC\), \(PB\) a \(PD\). Potom túto štvoricu priamok nazývame harmonický zväzok, pokiaľ body \(A, C, B, D\) sú v harmonickom štvorpomere.
Tvrdenie 1: Ak je štvorica priamok pretínajúca sa v bode \(P\) harmonickým zväzkom (teda existuje štvorica bodov \(A, C, B, D\) ležiacich na samostatnej priamke neprechádzajúcej bodom \(P\), ktorá je v harmonickom štvorpomere), potom priesečníky ľubovoľnej priamky neprechádzajúcej bodom \(P\), s týmto harmonickým zväzkom sú v harmonickom štvorpomere. Ako dôsledok, majúc dve priamky, \(m\) a \(n\) pretínajúce sa s štvoricou priamok \(p\), \(q\), \(r\), \(s\) prechádzajúcou bodom \(P\) v štvoriciach bodov postupne \(M_1\), \(M_2\), \(M_3\), \(M_4\) a \(N_1\), \(N_2\), \(N_3\), \(N_4\), potom jedna štvorica bodov je v harmonickom štvorpomere práve vtedy, keď je tá druhá.
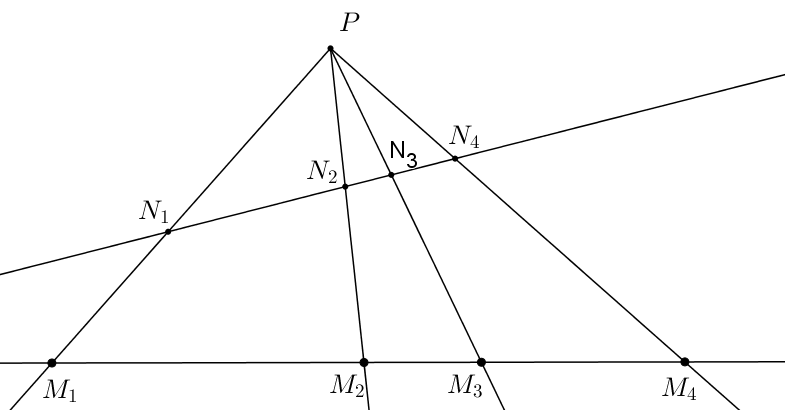
Tvrdenie 2: Uvažujme štvoricu priamok v harmonickom zväzku prechádzajúcu spoločným bodom \(P\) a uvažujme priamku \(a\) neprechádzajúcu \(P\). Nech priamka \(a\) pretína prvé tri priamky harmonického zväzku v bodoch \(A, C, B\). Potom \(C\) je stredom úsečky \(AB\) práve vtedy, keď štvrtá priamka zväzku je rovnobežná s priamkou \(a\).
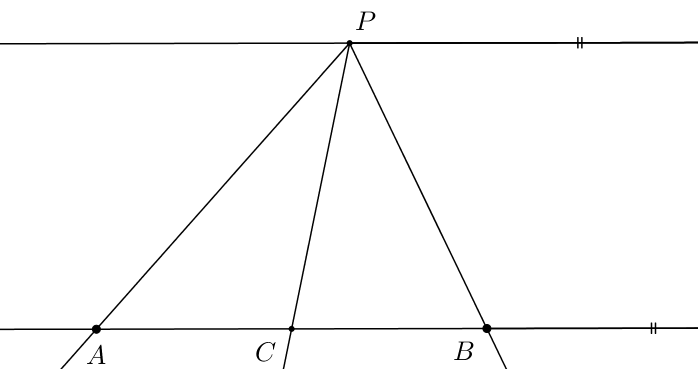
Tvrdenie 3: Majme bod \(P\), z neho vychádzajúce štyri priamky a na týchto priamkách body \(A, C, B, D\) ležiace v tomto poradí na ďalšej priamke (neprechádzajúcej \(P\)). Potom z nasledujúcich troch tvrdení platnosť ľubovoľných dvoch implikuje platnosť tretieho:
Priamka \(PC\) je osou uhla \(APB\).
Priamky \(PC\) a \(PD\) sú na seba kolmé.
Body \(A, C, B, D\) sú v harmonickom štvorpomere.
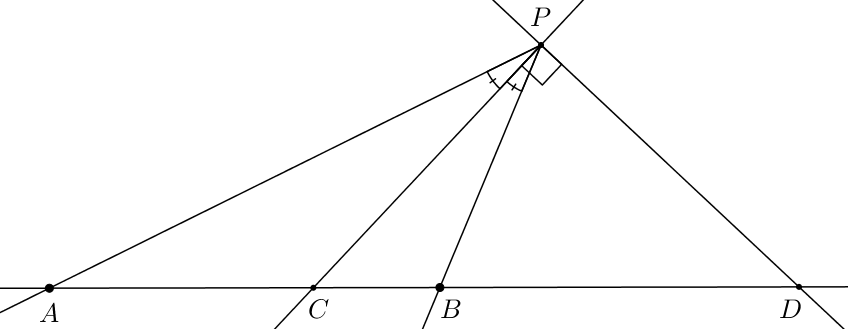
Teraz už vieme dosť na to, aby sme vedeli vyriešiť úlohu za pomoci harmonického štvorpomeru. Ak ste úlohu nevyriešili doteraz, ale chceli by ste tomu ešte dať šancu, teraz máte dobrú príležitosť prestať čítať vzorák a skúsiť úlohu vyriešiť s predošlými tvrdeniami. Každopádne, vzorák bude aj tak pokračovať.
Súc sugestívne vybrané práve tieto tri tvrdenia, chceme ich nejako využiť v tomto príklade. Cieľom je ukázať rovnobežnosť priamok, preto by sme mali využiť tvrdenie 2. Vidíme, že priamky \(CA\), \(CM\), \(CB\) a \(CK\) sú dobrými kandidátmi na harmonický zväzok, pretože nakoľko \(M\) je stredom úsečky \(AB\), majúc, že spomínané štyri priamky sú harmonický zväzok, rovnobežnosť \(AB\) a \(CK\) by priamo vyplývala z tvrdenia 2.
Na to, aby sme ukázali harmonickosť zväzku by sme potrebovali nájsť takú priamku, že o jej priesečníkoch s priamkami \(CA\), \(CM\), \(CB\) a \(CK\) by sme vedeli ukázať, že ležia v harmonickom štvorpomere. Potom s využitím tvrdenia 1 a definície by sme vedeli, že tieto štyri priamky sú harmonickým zväzkom a akákoľvek iná priamka, ktorá ich pretína vytvorí z priesečníkov harmonickú štvoricu (hoci v našom prípade je cieľová priamka \(AB\), ktorej prieniky s potenciálnym harmonickým zväzkom budú \(A\), \(M\), \(B\) a nekonečno). Máme len dve prirodzené možnosti na takúto priamku - \(ED\) alebo \(IK\). Vidíme však, že \(IK\) má oveľa viac odveci priesečníky, preto si vyberieme priamku \(ED\).
Označme \(P\) priesečník \(CM\) a \(ED\). O bodoch \(E, P, D, K\) chceme ukázať, že ležia v harmonickom štvorpomere. Mohli by sme využiť tvrdenie 3, avšak na to potrebujeme nájsť vhodný bod mimo priamky \(ED\), ktorý použijeme. Tu máme niekoľko možností. \(C\) nám nepomôže, pretože \(CP\) a \(CK\) rozhodne nie sú vo všeobecnosti kolmé. Podobne \(I\) nie je vhodný kandidát, nakoľko os uhla \(DIE\) je \(IC\) a nie \(IP\) ako by sme potrebovali (\(IC\) je osou uhla \(DIE\), lebo \(CEID\) je známy tetivový deltoid). \(M\) nie je vhodný kandidát, lebo jednak \(MP\) a \(MK\) nie sú vo všeobecnosti kolmé (dá sa všimnúť z obrázka), ale tiež preto, lebo tvrdenie, že \(MP\) by malo byť vo všeobecnosti osou uhla \(DME\) je príliš absurdné.
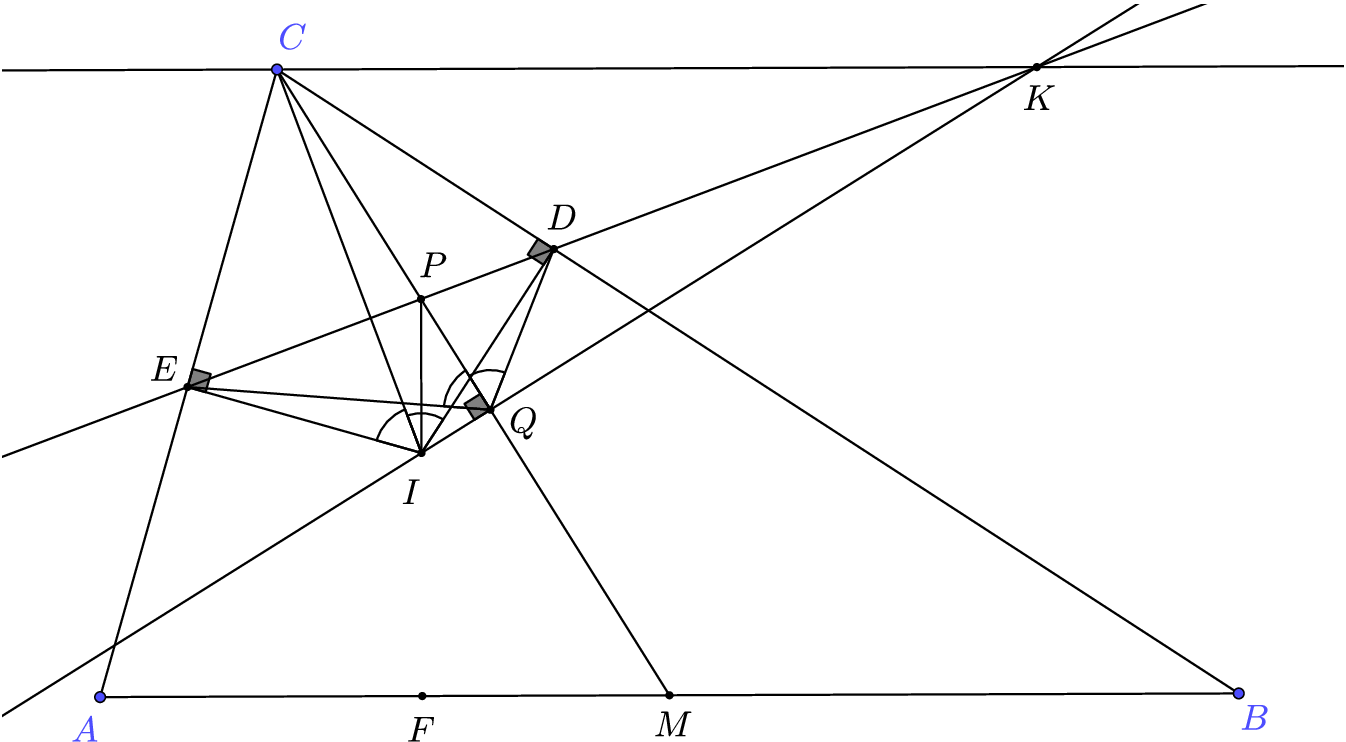
Ostáva nám už iba priesečník \(IK\) a \(CM\), bod, ktorý si označíme \(Q\). 3. Kolmosť \(PQ\) a \(QK\) máme priamo zo zadania, čo je ďalšia motivácia pozerať sa práve na tento bod. Ostáva nám ukázať, že \(QP\) je osou uhla \(DQE\). Konečne sa dostaneme k troche uhlenia. Bez ujmy na všeobecnosti, nech konfigurácia je taká, ako na obrázku, teda že \(I\) leží v polrovine \(CMA\). V opačnom prípade by bola argumentácia analogická (prípad \(I\) leží na \(CM\) je vylúčený zo zadania). Nakoľko uhol \(IQC\) je pravý, ako aj uhol \(IEC\), štvoruholník \(CEIQ\) je tetivový. Potom uhly \(EIC\) a \(EQC\) majú rovnakú veľkosť vďaka vete o obvodových uhloch.
Podobne, nakoľko \(CQI\) a \(CDI\) sú oba pravé, vidíme, že \(CIQD\) je tetivový. Potom uhly \(DQC\) a \(DIC\) majú rovnakú veľkosť. Už sme si ale povedali, že \(CI\) je osou uhla \(DIE\). Vidíme, že teda aj \(QP\) je osou uhla \(DQE\). Teraz využijeme tvrdenie 3 a zisťujeme, že body \(E, P, D, K\) ležia v harmonickom štvorpomere, čo je presne to, čo nám ešte chýbalo k vyriešeniu úlohy.
https://prase.cz/library/Harmonicky4PomerTP/Harmonicky4PomerTP.pdf↩︎
https://prase.cz/library/HarmonickectvericeDH/HarmonickectvericeDH.pdf↩︎
z obrázka sa dá vidieť, že máme malé \(IQ\)↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.