Zadanie
„Jubilár, ty chrbtobodajúci chrcheľ!“ zareval som na breh, keď nás zobudila salva šípov. Žiaľ, jeden šíp sa počas letu zabstrahoval na Navier-Stokesove rovnice, ktoré pokrkvali bezbranného Matrodeja ako prázdnu plechovku od gumidžúsu a ešte s ním šmarili niekoľko kilometrov proti prúdu. Videl som, ako mu pri tom vypadol z vrecka Konkretizátor a padol do vody. Schmatol som Krutitruľa za rukáv a vrhol som sa do Červenej rieky, aby som Konkretizátor vylovil, no ako som padal, hladina rieky sa zákerne zabstrahovala na akýsi štvoruholník a ja som musel bleskovo uvažovať.
V štvoruholníku \(ABCD\) platí \(|AD| = |AB| + |CD|\). Osi uhlov \(BAD\) a \(ADC\) sa pretínajú v bode \(P\). Dokážte, že platí \(|BP| = |CP|\).
Tento vzorák si môžete pozrieť aj vo videopodobe: https://youtu.be/tK8I4mn9CgI
Najprv sa zamyslíme, čo nám hovorí vzťah o súčte \(|AB|+|CD|=|AD|\), a ako si ho môžme vyjadriť geometricky. Jeden spôsob, ktorý sa hneď preukáže byť veľmi užitočný, je uvedomenie, že na stranu \(AD\) môžme umiestniť bod \(X\) tak, že \(|XA|=|AB|,|XD|=|CD|\). Teraz je načase narysovať si osi uhlov \(BAD\) a \(ADC\), nájsť bod \(P\), a narysovať úsečky \(PC\) a \(PB\). A ešte si narysujme úsečku \(PX\), lebo sa nám hneď preukáže byť užitočná:
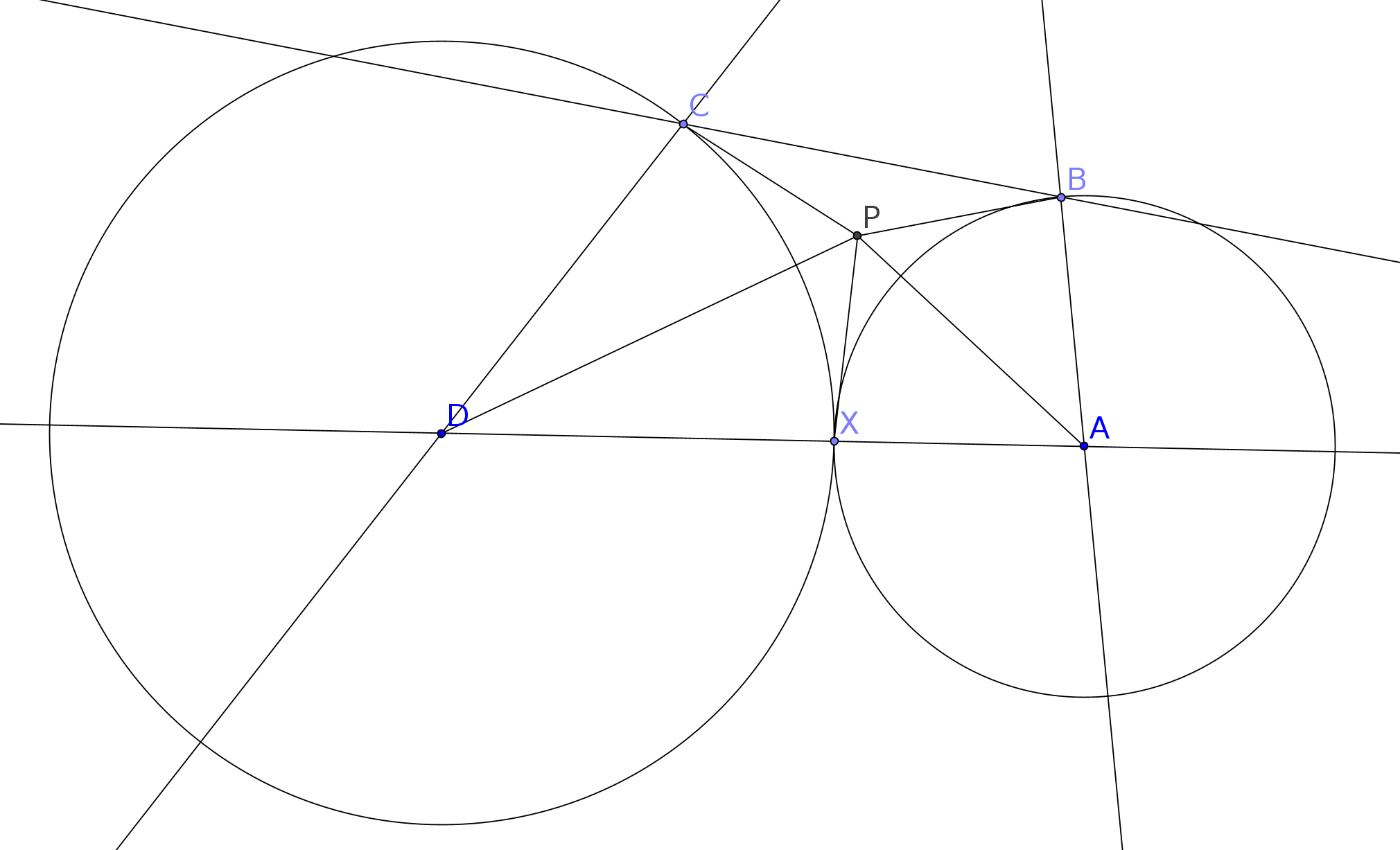
Pozrime sa teraz na trojuholníky \(APX\) a \(APB\). Keďže \(|AX|=|AB|\), \(|\sphericalangle XAP|=|\sphericalangle PAB|\) a stranu \(AP\) zdieľajú, vidíme, že sú zhodné. Z toho vidíme, že \(|PX|=|PB|\).
Ten istý argument funguje pre trojuholníky \(DPX\) a \(DPC\), z ich zhodnosti vidíme, že \(|PC|=|PX|\). A keďže \(|PC|=|PX|=|PB|\), vidíme, že \(|PC|=|PB|\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.