Zadanie
Keď už šervírka ščítala všetky položky dokopy, Mišom nezoštalo nič iné, ako zaplatiť všetci špolu. Ktorý Mišo však bude platiť?
Predša lichobežník \(MI\check{S}O\), v ktorom \(MI \parallel \check{S}O\) a \(|\sphericalangle \check{S}IM| < |\sphericalangle IMO| < 90^\circ\). Nech \(R\) je priešečník jeho uhlopriečok \(M\check{S}\) a \(IO\) a \(A\) je priešečník kružnice opíšanej trojuholníku \(RIM\) šo štranou \(I\check{S}\). Priamka \(OA\) pretína priamku \(MI\) v bode \(L\) a priamka \(MA\) pretína priamku \(O\check{S}\) v bode \(N\). Dokážte, že \(NR\) je dotyčnicou kružnice opíšanej trojuholníku \(RIM\) práve vtedy, keď je \(MR\) dotyčnicou kružnice opíšanej trojuholníku \(MAL\).
Vzorové riešenie tejto úlohy si môžeš pozrieť aj ako video na našom YouTube kanáli https://www.youtube.com/KorMatSem.
V zadaní ste si mohli všimnúť netradičnú požiadavku – dokázať, že niečo platí práve vtedy, keď platí niečo iné. Ide o výrok, ktorému sa hovorí ekvivalencia, to znamená že z prvej znalosti vyplýva druhá a z druhej prvá. Ekvivalenciu zo zadania dokážeme dokázaním implikácie oboma smermi, alebo po slovensky, v skutočnosti musíme riešiť dve úlohy – jednu, v ktorej máme zadané, že \(MR\) je dotyčnicou kružnice nad trojuholníkom \(MAL\) a potrebujeme dokázať dotykovosť \(NR\) ku kružnici nad \(MRAI\) – a druhú, v ktorej máme zadané že \(NR\) je dotyčnicou kružnice nad \(MRAI\) a potrebujeme dokázať dotykovosť \(MR\) ku kružnici nad \(MAL\). Až keď budeme mať dokázané obe úlohy, budeme vedieť povedať, že musia platiť naraz.
Pri úlohe nám opäť budú stačiť len znalosti o tetivových štvoruholníkoch a úsekovom uhle.
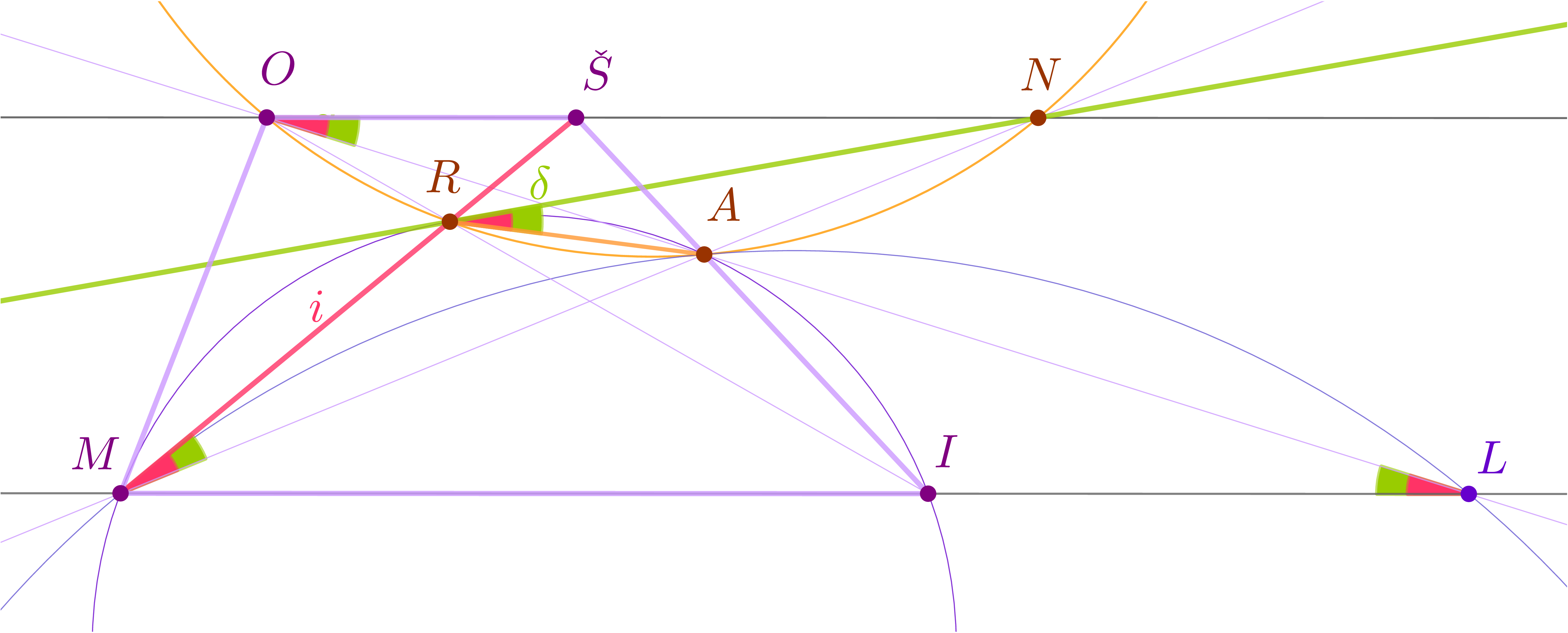
Začnime časťou pre obe úlohy rovnakou – štvoruholníkom \(ORAN\). Z rovnobežiek \(ON\) a \(ML\) a striedavosti uhlov vieme, že \(|\sphericalangle IMA|=|\sphericalangle ANO|\). Z vety o obvodových uhloch v už známom tetivovom štvoruholníku \(MRAI\) vieme, že \(|\sphericalangle IMA|=|\sphericalangle IRA|\) (\(=|\sphericalangle ANO|\) ). Uhol \(ORA\) dopočítame ako \(180^\circ-|\sphericalangle IRA|= 180^\circ-|\sphericalangle ANO|\). Teraz sa pozrime na súčet protiľahlých vnútorných uhlov v \(ORAN\)ovi, teda \(|\sphericalangle ANO|+|\sphericalangle ORA|=|\sphericalangle ANO|+180^\circ-|\sphericalangle ANO|=180^\circ\), teda \(ORAN\) je tetivový.
Poďme sa najskôr pozrieť na prvý prípad – chceme dokázať, že \(NR\) je dotyčnicou kružnici nad \(MRAI\). Vieme, že \(MR\) je dotyčnicou ku kružnici nad \(MAL\), uhol \(RMA\) teda bude úsekovým k obvodovému \(MLA\), čiže \(|\sphericalangle RMA|=|\sphericalangle MLA|=\alpha\). Z rovnobežnosti \(ON\) a \(ML\) vidíme, že uhly \(MLA\) a \(AON\) sú striedavé, čiže \(|\sphericalangle MLA|=|\sphericalangle AON|=\alpha\). Už vieme, že \(ORAN\) je tetivový, teda uhol \(NRA\) je obvodový uhol k uhlu \(AON\), čiže \(|\sphericalangle AON|=|\sphericalangle NRA|=\alpha\). Keďže \(|\sphericalangle RMA|=\alpha\) je obvodovým uhlom nad tetivou \(RA\) v štvoruholníku \(MRAI\), a keďže \(|\sphericalangle RMA|=|\sphericalangle NRA| = \alpha\), uhol \(NRA\) je úsekovým uhlom k tomuto obvodovému, a teda \(NR\) je dotyčnicou kružnice nad \(MRAI\).
Poďme na to teraz druhou stranou, vieme že \(NR\) je dotyčnicou kružnice nad \(MRAI\) a chceme dokázať, že \(MR\) je dotyčnicou kružnici nad \(MAL\). Obdobne, využijeme striedavosť uhlov \(AON\) a \(MLA\), \(|\sphericalangle AON|=|\sphericalangle MLA|=\beta\). V tetivovom štvoruholníku \(ORAN\) je uhol \(NRA\) obvodový k uhlu \(AON\), \(|\sphericalangle NRA|=|\sphericalangle AON|=\beta\). Keďže \(NR\) je dotyčnicou ku kružnici nad \(MRAI\), uhol \(NRA\) je úsekový k tetive \(RA\), teda obvodový \(|\sphericalangle RMA|=|\sphericalangle NRA|=\beta\). Keďže \(|\sphericalangle MLA|=|\sphericalangle RMA|=\beta\), uhol \(RMA\) musí byť úsekový, teda \(MR\) je dotyčnicou kružnice nad \(MAL\).
Oboma dôkazmi sme teda dokázali ekvivalenciu zo zadania.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.