4. Kužele Ma Smädia vzorové riešenie

Palko[email protected] Mati[email protected]

V zadaní na nás čakala trojrozmerná dvojhlavá chmára. My sa jej však nezľakneme. Môžeme si rýchlo všimnúť, že veľa jej častí je rotačne súmerných, čo s výhodou využijeme v náš prospech. S trojrozmernými chmárami sa zapasí vcelku ťažko, tak by sme ju radi dostali na papier. Pamätajúc na jej súmernosti si zvoľme rovinu, v ktorej sa nachádzajú obe osi súmernosti kužeľov, a porazme chmáru v nej. Takže sa nám kužele zmenili na trojuholníky, ktorých podstavy sú na seba kolmé a zdieľajú jediný bod (lebo osi súmernosti kužeľov boli na seba kolmé a ich priesečník bol vzdialený od podstáv \(3\), čo je aj polomer podstavy). Označme ho \(A\). Teraz sa môžeme pustiť do poriadneho boja.

Najväčšia kružnica bude mať stred na priesečníku osí

Najprv najväčšia kružnica, ktorá sa dá vpísať chmáre do brucha (oblasti, ktorá patrí obom jej kužeľom) má stred v priesečníku osí súmernosti \(E\), čo si ukážeme nižšie.

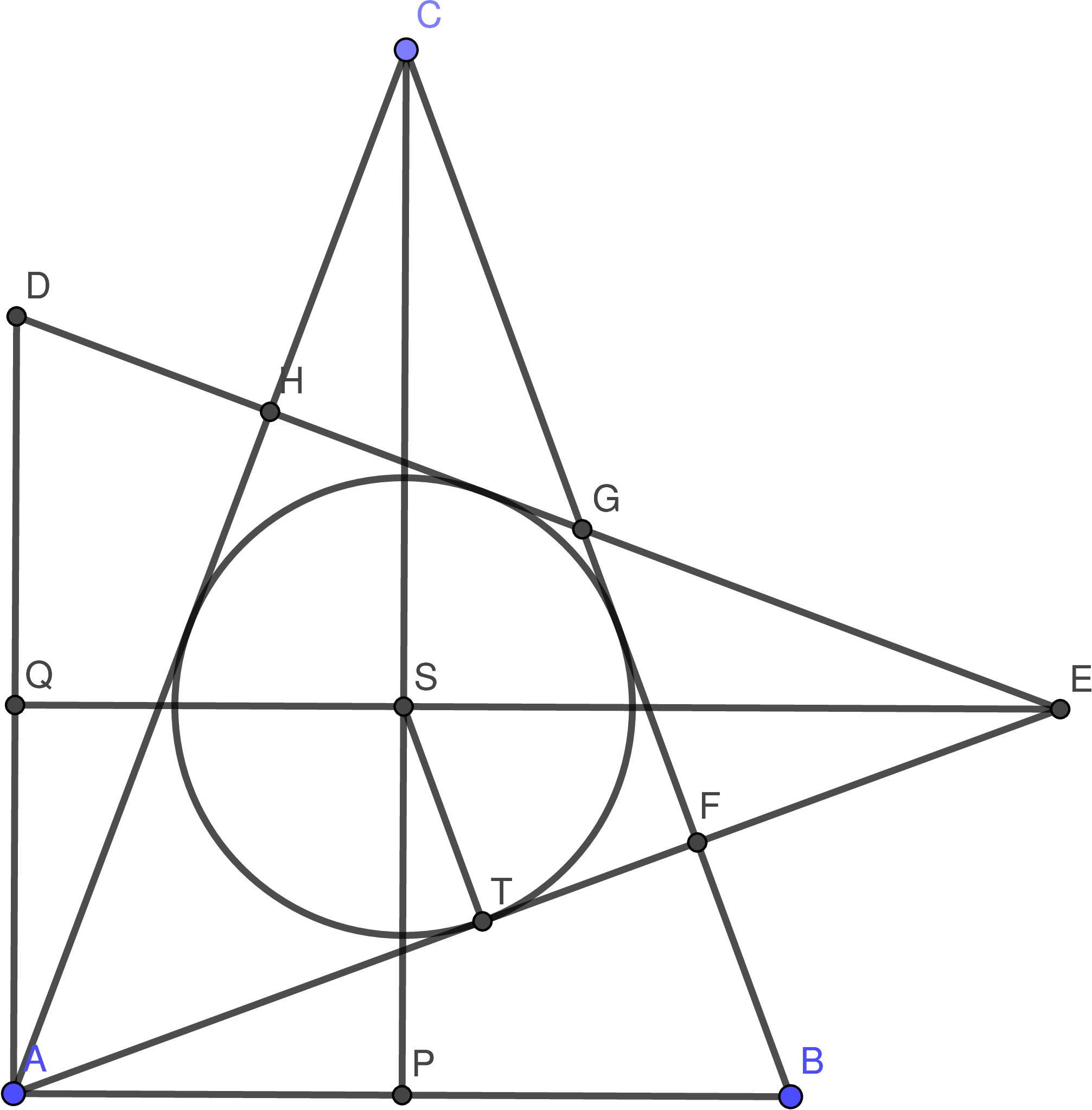
Keď chmáre zmeriame brucho, zistíme, že to je deltoid¹ (\(AFGH\)). Je to pekne vidieť zo súmernosti podľa osi \(AG\), vďaka tomu \(|AF|=|AH|\) a \(|FG|=|HG|\). Deltoidu vieme vpísať práve jednu kružnicu, lebo je dotyčnicový (\(|AF| + |GH| = |AH| + |FG|\), každý štvoruholník, ktorého súčty protiľahlých strán sú rovnaké, je dotyčnicový, skúste si to sami rozmyslieť).

Začnime s jednoduchšou situáciou – budeme sa tváriť, že nemáme stranu \(GH\). Ostal nám trojuholník \(AFC\), pre ktorý chceme nájsť najväčšiu kružnicu, ktorá sa do neho zmestí. Je známe, že pre trojuholník to je kružnica vpísaná. Keď máme vpísanú kružnicu, vráťme späť stranu \(GH\). Dostali sme deltoid, ktorý je menší ako pôvodný trojuholník, teda nebude sa mu dať vpísať väčšia kružnica. Nakoniec ak sa kružnica už dotýka troch strán deltoidu, (\(AF\), \(FG\), \(AH\)), tak jej stred leží na osiach uhlov \(AFG\) a \(FAH\). Na nich leží aj stred kružnice deltoidu vpísanej. Obe kružnice majú teda rovnaký stred a zároveň sa dotýkajú rovnakej strany \(AH\), tak to už nemôže dopadnúť inak, ako že budú zhodné.

Teraz už ľahko nahliadneme, že vďaka tomu, že naša kružnica sa dotýka úsečky \(GF\), tak sa dotýka aj úsečky \(BC\) a vďaka tomu, že sa dotýka úsečky \(AH\), tak sa bude primykať aj k úsečke \(AC\). Vzdialenosť stredu od oboch priamok je vďaka tomu rovnaká a stred bude na osi uhla \(ACB\). Analogicky pre uhol \(DEA\). Yes, tak sme sa chmáre konečne dostali pod kožu.

To už sa dáko ubije

Keď teraz vieme, že vpisujeme kružnicu do prieniku rovnoramenných trojuholníkov, a ešte k tomu, že jej stred je v priesečníku ich osí súmernosti, stačí nám chmáru nejak dorátať do úspešného konca. Existuje na to viacero spôsobov, tu si ukážeme výpočet cez podobnosť trojuholníkov a Pytagorovu vetu (čo je, technicky vzaté, tiež len podobnosť trojuholníkov).

Označme si trojuholníky a kružnicu tak ako na obrázku, \(T\) je bod dotyku kružnice so stranou \(AE\) a \(S\) je stred kružnice. Priamka \(QE\) je os súmernosti trojuholníka \(ADE\), a teda je kolmá na stranu \(AD\). Pozrime sa na trojuholníky \(AEQ\) a \(SET\). Majú spoločný uhol pri vrchole \(E\) a tiež každý má jeden pravý uhol – väčší trojuholník ho má pri vrchole \(Q\) a menší pri vrchole \(T\) (to je bod dotyku kružnice s \(AE\), a teda \(AE\) je kolmá na polomer \(ST\)). Na základe toho vieme povedať, že sú podobné. Teraz využijeme známe vzdialenosti a dorátame z nich polomer kružnice. Zo zadania vieme, že \[\begin{aligned} &|AQ|=|QS|=3, \\ &|QE|=8, \\ &|SE|=|QE|-|QS|=8-3=5.\end{aligned}\]

Teraz nám stačí si vybrať správne rovnosti z tých, ktoré nám ponúka podobnosť trojuholníkov. Zvoľme napríklad \[\frac{|ST|}{|SE|}=\frac{|AQ|}{|AE|}.\] Odkiaľ môžeme vyjadriť polomer kružnice \(ST\) ako \[r=|ST|=|SE|\cdot\frac{|AQ|}{|AE|}\] a máme hotovo. ...ojha! Chýba nám veľkosť strany \(AE\). Tú ale vieme veľmi ľahko zrátať, keďže trojuholník \(AQE\) je pravouhlý a poznáme jeho obe odvesny. Máme teda \[|AE|=\sqrt{3^2+8^2}=\sqrt{73}.\] Dosadíme do vzťahu pre \(r\) a máme výsledok \[r=5\cdot\frac{3}{\sqrt{73}}=\frac{15}{\sqrt{73}}.\]

Našli sme najväčšiu kružnicu, ktorá sa zmestí do brucha dvojrozmernej chmáry. Ako nám to pomôže s chmárou trojrozmernou? Roztočme jeden trojuholník podľa jeho osi. Dostali sme kužeľ s guľou vnútri. Táto guľa určite z neho nevytŕča, pretože v každom momente otáčania kružnica z trojuholníka nevytŕčala. V tomto kuželi guľa nie je najväčšia možná, je však najväčšia možná spomedzi tých, ktoré sa zmestia do kužeľa a rovnoramenného trojuholníka, ktorý sme ešte nezrotovali. Ostáva nám ešte zistiť, či nám nevytŕča z druhého kužeľa. Ajhľa, keď zrotujeme druhý kužeľ okolo jeho osi, v každom momente sa bude gule dotýkať, takže z nej nikde trčať nebude. Dostali sme presne to, čo sme chceli – skrotili sme chmáru.