10. Kilometrov Maťko Spravil vzorové riešenie

Zlodejka[email protected] Maťko „Vodka“ Vodička[email protected]

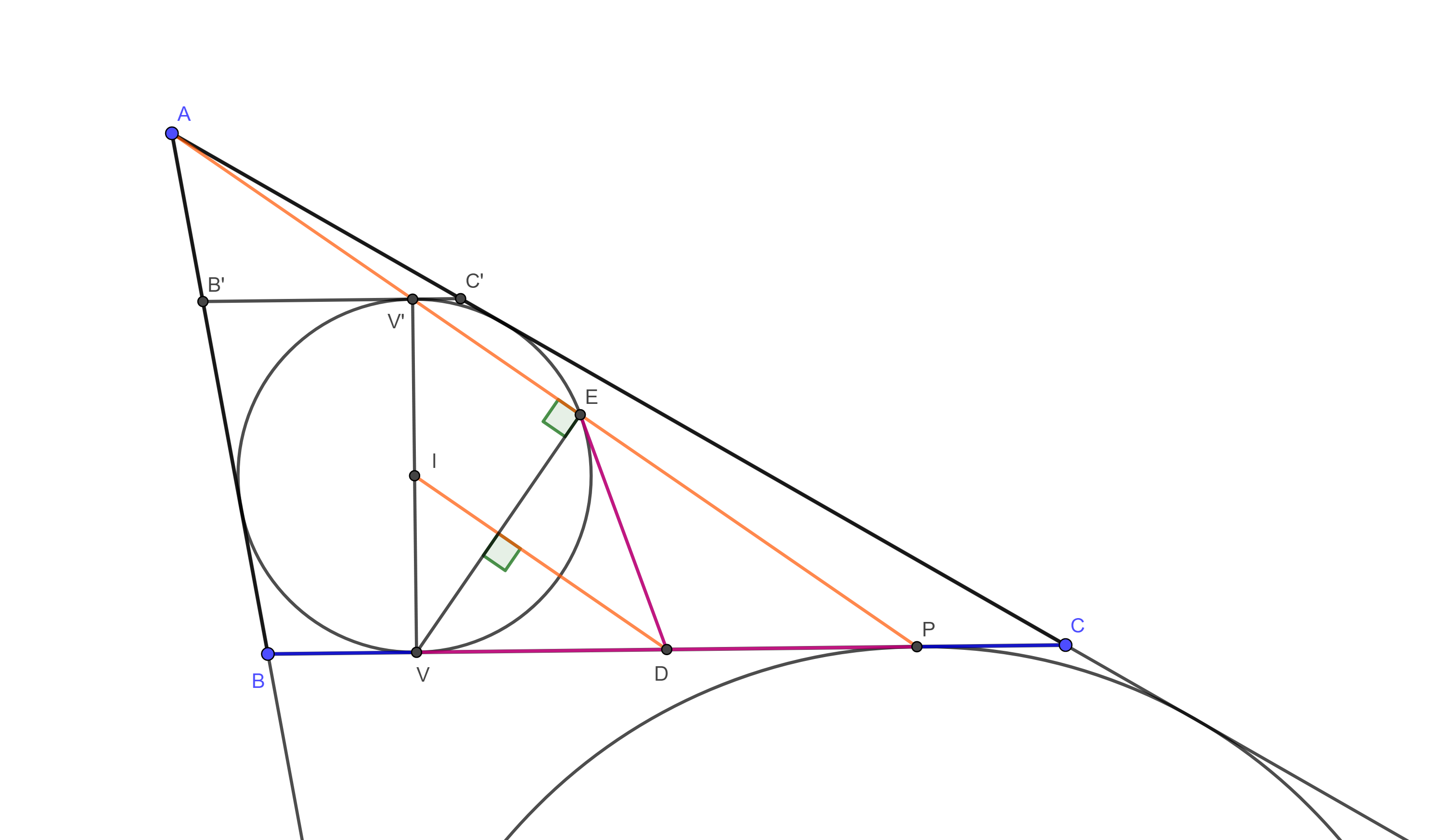
Označme \(V\) bod dotyku \(BC\) a vpísanej kružnice. Nech \(V'\) je druhý priesečník priamky \(VI\) a vpísanej kružnice, takže \(VV'\) je jej priemer. Ďalej označme bod dotyku \(BC\) a \(A\)-pripísanej kružnice \(P\). (\(A\)-pripísaná kružnica je taká, ktorá sa dotýka \(BC\) z vonkajšej strany a priamok \(AB\) a \(AC\).)

Ukážeme, že \(A,\) \(V'\) a \(P\) ležia na jednej priamke.

Veďme rovnobežku s \(BC\) cez bod \(V'\) a označme priesečníky s \(\triangle ABC\) postupne \(B'\) a \(C'\). Platí, že \(\triangle ABC \simeq \triangle AB'C'\). Všimnime si, že úsečka \(BC\) sa dotýka vpísanej kružnice v bode \(V'\), lebo bod \(V'\) je „najvyššie položený bod“ na vpísanej kružnici, a teda vpísaná kružnica \(\triangle ABC\) je zároveň pripísanou kružnicou \(\triangle AB'C'\). Vďaka tomu sa \(\triangle AB'C'\) zobrazí v rovnoľahlosti so stredom v \(A\) na \(\triangle ABC\) a vpísaná kružnica na \(A\)-pripísanú. Bod \(V'\) sa takto zobrazí na \(P\). Z toho plynie, že body \(A,V'\) a \(P\) ležia na jednej priamke.

Nech \(E'\) je druhý priesečník priamky \(AV'\) s vpísanou kružnicou. Naším cieľom teraz bude ukázať, že \(E=E'\).

O bodoch dotyku pripísanej a vpísanej kružnice platí známe tvrdenie, a to že \(|BV|= |PC|\), z čoho dostávame, že aj \(|VD|=|DP|\), lebo \(D\) je stred strany \(BC\).

Ak toto tvrdenie nepoznáte, tak si ho môžete skúsiť dokázať: Nakreslite si všetky body dotyku vpísanej a pripísanej kružnice a skúste vyjadriť \(|BV|\) a \(|PC|\) pomocou dĺžok strán trojuholníka \(ABC\). Obe sú rovné \((|AB|+|BC|-|AC|)/2\). Využite, že ak z ľubovoľného bodu spustíme dve dotyčnice ku kružnici, tak vzdialenosť k dvom bodom dotyku je rovnaká.

Keďže \(VV'\) je priemer vpísanej kružnice, na ktorej leží aj \(E'\), tak uhol \(V'E'V\) je pravý (Tálesova veta). Z toho máme, že \(VE'P\) musí byť tiež pravý, teda \(\triangle V'EP\) je pravouhlý. Platí, že v pravouhlom trojuholníku je stred opísanej kružnice zároveň stredom prepony. Preto je \(D\) stred opísanej kružnice \(\triangle VE'D\) a z toho \(|VD|=|DE'|=|DP|\). To znamená, že \(V\) a \(E'\) sú dva body ležiace na vpísanej kružnici, ktoré sú rovnako vzdialené od bodu \(D\) a takéto body môžu byť len dva. Keďže \(VD\) je dotyčnica vpísanej kružnice, tak aj \(DE'\) musí byť dotyčnica. Z toho už vyplýva rovnosť \(E=E'\).

Posledným krokom je ukázať rovnobežnosť \(DI\) a \(AE\). Už sme ukázali, že body \(A,V',E,P\) ležia na jednej priamke a tiež, že \(D\) je stred \(VP\). Ďalej vieme, že \(I\) je stredom \(VV'\). Preto je \(DI\) stredná priečka \(\triangle VPV'\), čiže \(DI\) je rovnobežná z \(AE\). Tým je dôkaz hotový.