8. Kroky Mnohých Štolbov vzorové riešenie

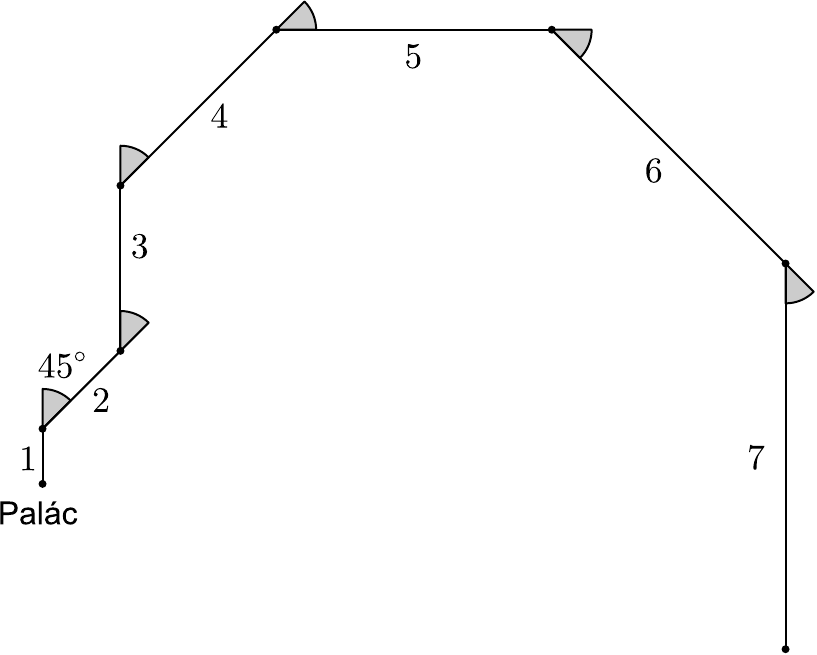
Pri úlohách, v ktorých treba rozhodnúť, či nejaké tvrdenie platí alebo nie, má riešiteľ vždy na výber medzi pesimistickým a optimistickým prístupom. Ja som túto úlohu začal riešiť pesimisticky a snažil som sa ukázať, že takáto cesta neexistuje. Prvá vec, ktorú som si všimol a ktorá je dôležitá je, že ak taká cesta existuje, potom časť tejto cesty, ktorá by vznikla pozliepaním iba horizontálnych alebo vertikálnych krokov by sama musela viesť z počiatku do počiatku. Podobne časť cesty zložená iba z diagonálnych krokov (pozliepaných na seba) by musela viesť z počiatku do počiatku. Prečo?

Predstavme si v našej rovine karteziánsku súradnicovú sústavu, ktorej počiatok \([0, 0]\) je v našom paláci. Kroky, ktoré robíme, si môžeme v tomto prípade prestaviť ako vektory, ktoré pričítavame k našej aktuálnej pozícii. Ak má diagonálny krok dĺžku \(a\), potom posun v horizontálnej a vertikálnej zložke bude \(a/\sqrt{2}\), čo vyplýva z Pytagorovej vety alebo z definície sínusu v pravouhlom trojuholníku. Všimnime si, že nech už naše kroky majú akýkoľvek smer, diagonálne kroky (t. j. vektory) sa budú musieť nasčítať na nulu samy o sebe a tak isto horizontálno-vertikálne kroky. Prečo? Iracionálnu časť \(1/\sqrt{2}\) si vieme v našich sčítancoch vyňať pred zátvorku a výraz, ktorý sa musí nasčítať na nulu má tvar \(p+(1/\sqrt{2})q\), kde \(p,\ q\) sú racionálne čísla. Ak sa tento výraz rovná \(0\), potom ľahko vidno, že aj \(p\) aj \(q\) musia byť samy rovné \(0\).

Takže ak by existovala takáto cesta, musela by existovať aj cesta zložená z krokov dĺžky \(1,\ 2,\ 3,\ \dots\), ktoré by mohli zvierať iba pravé alebo nulové uhly (skús si rozmyslieť, prečo to vyplýva z predošlého odstavca). Tu však naše pesimistické myšlienky končia. Akokoľvek sa totiž budeme snažiť, neprídeme na žiaden rozumný spôsob ako dokázať, že takáto cesta neexistuje. Pretože existuje. Keď už sa rozhodneme nejakú hľadať, nie je náročné ju nájsť.

Pri hľadaní konštrukcii ako napríklad cesty sa vždy hodí skúsiť sa pozrieť na nejaký ľahký vzor a zistiť, o koľko sme sa po odkráčaní tohto ľahkého vzoru posunuli od štartu. Ak má tento ľahký vzor vhodné vlastnosti, môžeme ho potom zopakovať a posunúť sa od našej aktuálnej pozície rovnako, ako sme sa predtým posunuli od štartu, ale možno do iného smeru. Naskladaním takýchto posunov sa snáď budeme vedieť vrátiť do štartu.

V prípade našej úlohy stačí skúsiť spraviť pravotočivého „slimáka“ o štyroch krokoch ako na obrázku 1 a môžeme si všimnúť, že po spravení tohto slimáka sme presne \([\pm 2, \pm 2]\) v nejakom smere od počiatku. Navyše, presne rovnaký posun by sme dosiahli bez ohľadu na to, v ktorom ťahu by sme tohto slimáka spravili. Prečo? V štyroch krokoch ideme raz doľava, raz doprava, raz nadol a raz nahor, avšak protismerné pohyby robíme s rozostupom dvoch ťahov, čo znamená že, dĺžky našich krokov sa dokonale vykompenzujú s výnimkou rozdielu dĺžky 2.

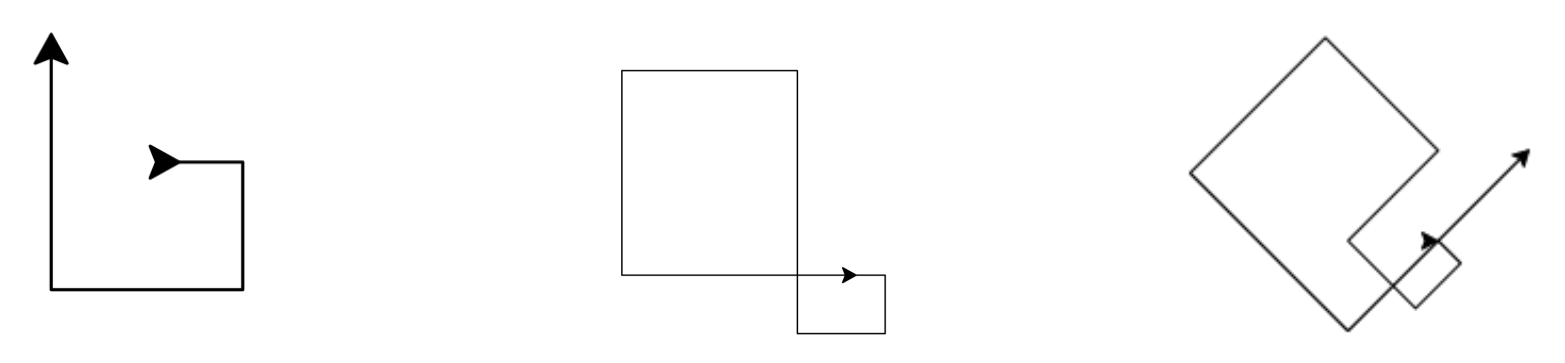
Teraz ak sa z pozície, v ktorej sme skončili po dokončení slimáka, vyberieme naspäť tak, že začneme v rovnakom smere ako sme skončili a slimáka spravíme ľavotočivého (ako na obrázku 1), dostaneme sa späť do počiatku. Hurá! Problém je, že toto je riešenie iba pre „polku“ našej prechádzky. Na to aby sme sa naozaj dostali do cieľa – teda štartu – potrebujeme vhodne skombinovať diagonálne a vertikálno-horizontálne slimáky. Skúsme si intuitívne skombinovať našu vertikálno-horizontálnu cestu s takou diagonálnou, ktorá do toho pasuje. Ak to spravíme (ako na obrázku 2), uvidíme, že nanešťastie sa tieto cesty nedajú skombinovať tak, aby diagonálna bola úplne analogická (čo vidno aj keď si zobrazíme iba diagonálnu časť tejto cesty, viď 1). Všetko je rovnaké, až na to, že v diagonálnej ceste odbočíme doľava pri zmene z pravotočivého na ľavotočivého slimáka. Našťastie, čo si môžeme všimnúť je, že po spravení celej tejto zvláštnej špirály sa dostaneme od počiatku na súradnice \([8, 8]\). Máme teda šancu opakovať tento istý vzor tak, aby sme sa po nejakom čase konečne dostali späť do cieľa.

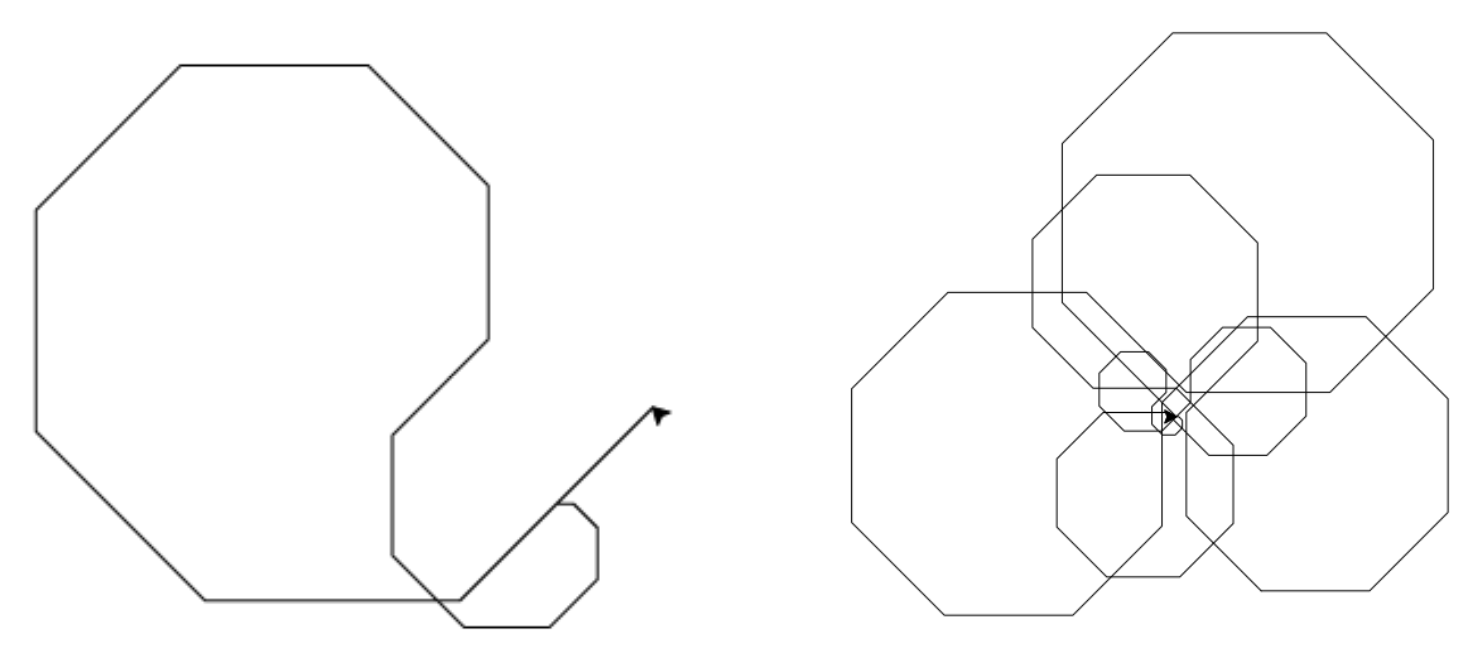
Odtiaľto už je finálna konštrukcia veľmi jednoduchá – stačí si všimnúť, že hneď po dokončení tohto vzoru sa vieme otočiť o \(45^\circ\) doľava a zopakovať náš vzor tak, aby sme sa od našej aktuálnej pozície posunuli smerom doľava nahor o rovnakú vzdialenosť ako predtým z počiatku. Po dokončení tohto vzoru sa opäť môžeme otočiť o \(45^\circ\) doľava a posunúť sa v pravom uhle od nášho predošlého posunu, tentoraz smerom dole doľava. V poslednom opakovaní sa posunieme o rovnakú vzdialenosť dole doprava a ocitneme sa v počiatku (viď obrázok 2).

Možno sa vám zdá, že tento popis cesty nie je úplne dôkaz, ale v podstate aj celkom je. Dôležitým prvkom našej cesty je, že sú to len štyri pootočené opakovania tej istej trajektórie, ktorá sa skladá zo štyroch slimáčikov, ktoré sa vždy posúvajú o 2 dohora alebo nadol a o 2 doľava alebo doprava. Preto analýzou toho, čo sa stane pri daných kombináciách našich slimákov, vieme naozaj jednoducho formálne dokázať toto tvrdenie vďaka tomu, že opakujeme ten istý vzor stále dokola.