Zadanie
Keď sa Krtkovi podarilo vyhrať nad starčekom, starčeka to natoľko napajedilo, že začal úbohého Krtka naháňať po trhovisku. Našťastie sa pred Krtkom zjavil portál a on celý natešený doň skočil, bez toho, aby vedel, kam ho prenesie. Portál Krtka vypľul na Artušov okrúhly stôl. Zaskočený Artuš sa hneď dovtípil, že Krtko nebude miestny a rozhodol sa, že si Krtka nechá ako svojho tajného poradcu. Zavrel ho preto do kumbálu na metly a začal sa radiť so svojimi rytiermi, ako s Krtkom naložia. Krtkovi tam bolo už dlho a aj sa poriadne nudil. Tak si sadol do vedra a zapozeral sa na stenu oproti.
Tu si všimol, že stena sa skladá z kachličiek v tvare šesťuholníkov uložených v \(2\) riadkoch po \(n\) kachličiek, ako na obrázku. Krtko položil prst na kachličku vľavo dole. V každom kroku posunie prst na susednú kachličku, ktorá je od nej vpravo hore, vpravo, alebo vpravo dole. Koľko je rôznych kachličiek, na ktorých môže mať Krtko prst po presne \(n\) krokoch? Na obrázku nižšie sú nakreslené kachličky pre prípad \(n=4\), na sivej kachličke Krtko začína a modrou je vyznačená jedna možná cesta.
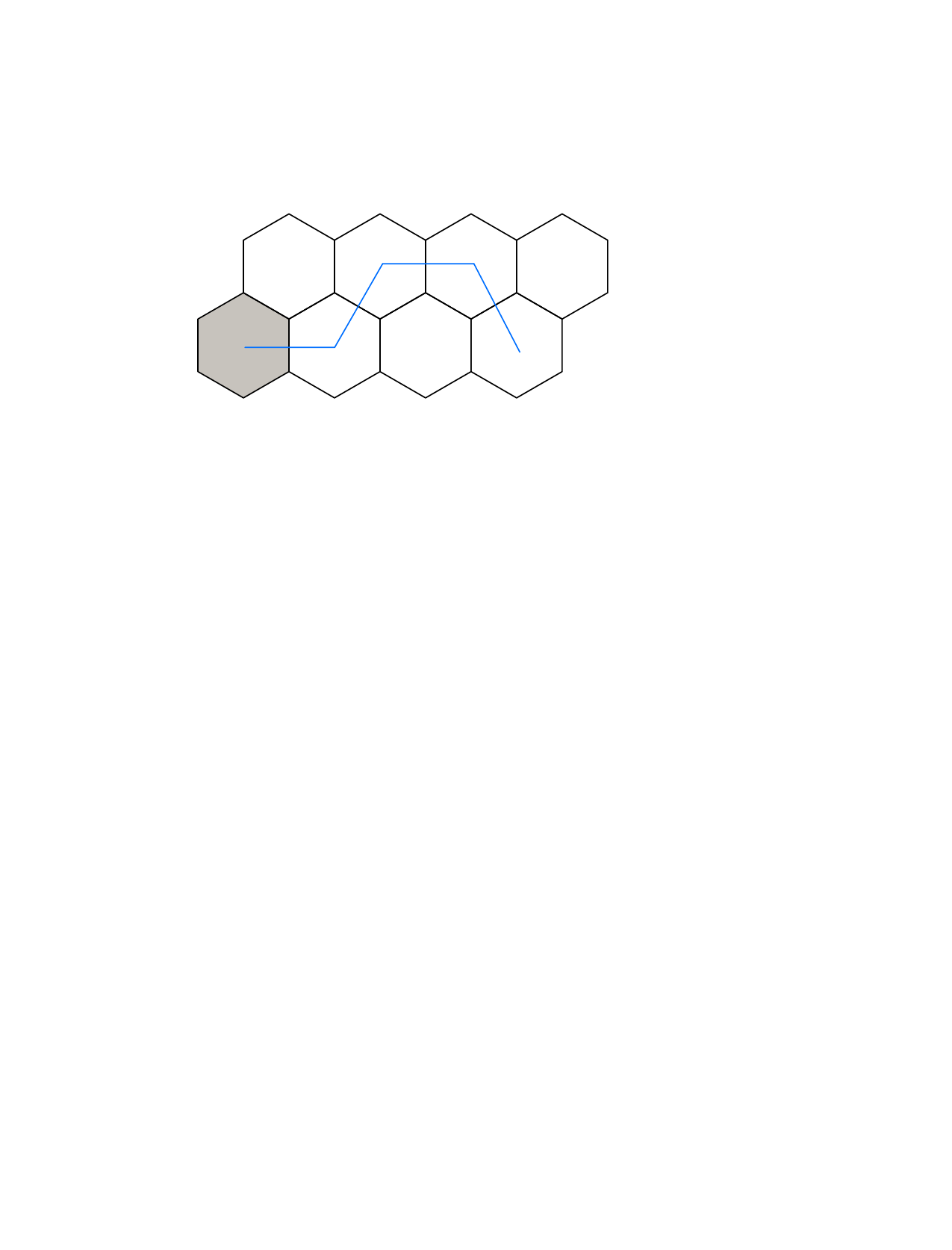
Kachličky v dolnom riadku si predstavíme ako po sebe idúce párne čísla začínajúce od čísla \(0\). Kachličky v hornom riadku budú predstavovať po sebe idúce nepárne čísla začínajúce od čísla \(1\).
Keď sa nachádzame na čísle \(k\), môžeme vykonať dva ťahy. Môžeme ísť na číslo \(k + 1\) (tento ťah reprezentuje prechod na kachličku v opačnom riadku) alebo môžeme prejsť na číslo \(k + 2\) (tento ťah zas reprezentuje prechod na kachličku v tom istom riadku).
Ako sa dá na takéto označenie prísť a prečo by sme ho vôbec hľadali? Odpoveď na druhú otázku je, že je fajn si popísať úlohu formálnejším spôsobom ak nie je príliš zložitý. Môže nám to totiž pomôcť všimnúť si vlastnosti, ktoré by ináč zostali nepovšimnuté. A teda prirodzené čísla sú pri takomto popisovaní často veľmi užitočné. Odpoveď na prvú otázku – stačilo kachličky očíslovať (prvá kachlička v dolnom riadku má číslo \(0\), prvá kachlička v hornom riadku číslo \(1\), atď.).
Chceme odpovedať na otázku: ak začíname na čísle nula a vykonáme \(n\) ťahov, na koľkých rôznych políčkach sa môžeme nachádzať? Označme číslo, na ktorom sa budeme nachádzať po \(n\) krokoch ako \(k\). Aká je najmenšia možná hodnota \(k\)?
Zjavne \(k \geq n\), keďže musíme vykonať presne \(n\) ťahov a každý ťah nás posunie na číslo aspoň o \(1\) vyššie. Zjavne na číslo \(n\) sa vieme dostať tým, že \(n\)-krát vykonáme ťah prvého typu.
Aká je najväčšia možná hodnota \(k\)? Zjavne \(k \leq 2n - 1\), keďže kachlička s vyšším číslom neexistuje. Na číslo \(2n - 1\) sa vieme dostať pomocou \(n - 1\) ťahov druhého typu a jedného ťahu prvého typu.
Teda pre všetky \(k\), na ktoré sa vieme dostať po presne \(n\) ťahoch, platí \(n \leq k \leq 2n - 1\). Majme nejaké \(k\), ktoré spĺňa poslednú podmienku. Dokážeme, že sa na toto číslo vieme dostať pomocou \(n\) ťahov.
Vykonajme najprv \(k - n\) ťahov typu 2 a následne \(2n - k\) ťahov typu 1. Dokopy teda vykonáme \((k - n) + (2n - k) = n\) ťahov a na konci sa nachádzame na čísle \(2(k - n) + (2n - k) = k\).
To znamená, že na konci sa vieme nachádzať na ľubovoľnom prirodzenom čísle \(k\), pre ktoré platí \(n \leq k \leq 2n - 1\). Takých čísel je \(n\), a to je aj odpoveď na našu otázku.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.