Zadanie
Počas toho, ako sa vedúci sťažovali, sa Jožko prechádzal po okolí. Ako sa tak obzeral, zakopol o jednu zvláštnu hubu. Huba, o ktorú Jožko zakopol, mala klobúk v tvare trojuholníka . Nebol to ale obyčajný trojuholníkový klobúk.
V rovine je daný trojuholník \(ABC\). Pre jeho uhly platí \(|\sphericalangle ABC| = 2\cdot |\sphericalangle BAC|\). Taktiež na jeho strane \(AB\) leží bod \(D\) taký, že \(|\sphericalangle ACD| = |\sphericalangle BCD|\) a navyše \(|CD|=|BC|\). Určte veľkosť uhla \(\sphericalangle BAC\).
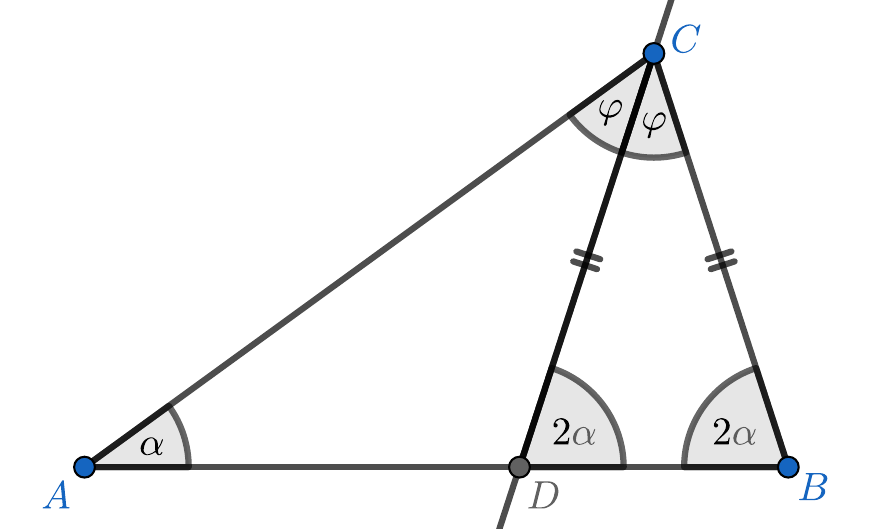
Označme si uhol \(BAC\) ako \(\alpha\) a uhol \(BCD\) ako \(\phi\).
Zo zadania vieme, že \(|\sphericalangle ABC| = 2\alpha\). Keďže \(|BC| = |CD|\), trojuholník \(BCD\) je rovnoramenný so základňou \(BD\), a teda platí \(|\sphericalangle CBD| = |\sphericalangle BDC| = 2\alpha.\) Keďže súčet uhlov v trojuholníku \(BCD\) je \(180^{\circ}\), musí platiť \[\begin{align} 2\alpha + 2\alpha + \phi &= 180^{\circ}, \nonumber \\ 4\alpha + \phi &= 180^{\circ}. \tag{1}\end{align}\]
Tiež vieme \(|\sphericalangle ACD| = |\sphericalangle BCD| = \phi\), odkiaľ \[|\sphericalangle ACB| = |\sphericalangle ACD| + |\sphericalangle BCD| = 2\phi.\]
Opäť, pretože súčet uhlov v trojuholníku \(ABC\) je \(180^{\circ}\), musí platiť \[\begin{align} \alpha + 2\alpha + 2\phi &= 180^{\circ}, \nonumber \\ 3\alpha + 2\phi &= 180^{\circ} \tag{2}.\end{align}\]
Rovnice \((1)\) a \((2)\) tvoria sústavu s neznámymi \(\alpha, \phi\). Riešením tejto sústavy dostaneme \(\alpha = \phi = 36^\circ\).
Odpoveď: veľkosť uhla \(BAC\) je 36 stupňov.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.