7. Kruh Mágie Sadu vzorové riešenie

V prvom rade nás asi bude zaujímať, kde sa bude nachádzať bod \(E\). Skúsenejší z nás v bode \(E\) hneď spoznajú Švrčkov bod trojuholníkov \(ABD\) a \(ACD\). Pre bežných smrteľníkov: je známe, že v trojuholníku sa os strany a os uhla oproti nej pretnú na kružnici tomuto trojuholníku opísanej v bode, ktorý sa nazýva Švrčkov bod (danej strany, resp. daného vrcholu oproti strane).¹

V tomto prípade máme stranu \(AD\) a nad ňou dva trojuholníky na rovnakej kružnici. Priesečník osi strany \(AD\) a kružnice je teda Švrčkov bod tejto strany a budú ním prechádzať osi uhla oproti AD v akomkoľvek trojuholníku nad \(AD\), a teda aj v \(ABD\) aj v \(ACD\).

Keď už vieme, že \(E\) bude na kružnici, poďme vyťažiť niečo z faktu \(|AB|=|BC|=|CD|\). O \(ABC\) aj \(BCD\) vieme, že sú rovnoramenné, teda majú rovnaké uhly pri základni: \(\sphericalangle BAC = \sphericalangle BCA\) a \(\sphericalangle CBD = \sphericalangle CDB\). A keďže \(\sphericalangle BAC\) je obvodový ku \(\sphericalangle BDC\) vieme, že všetky 4 tieto uhly sú zhodné, nazvime ich \(\alpha\).

Teraz príde čas uvedomiť si, že úloha môže mať dve konfigurácie. Ak by totiž bola vzdialenosť \(|AB|\) dosť veľká, môže sa stať, že bod \(D\) bude medzi \(A\) a \(B\). Konkrétne, keď sú od seba vzdialené viac ako tretinu kružnice, \(D\) už bude za \(A\). Vtedy sa úsečky \(AB\) a \(CD\) budú pretínať, inak sa pretínať nebudú. Poďme sa najskôr pozrieť na tú, kde sa nepretínajú.

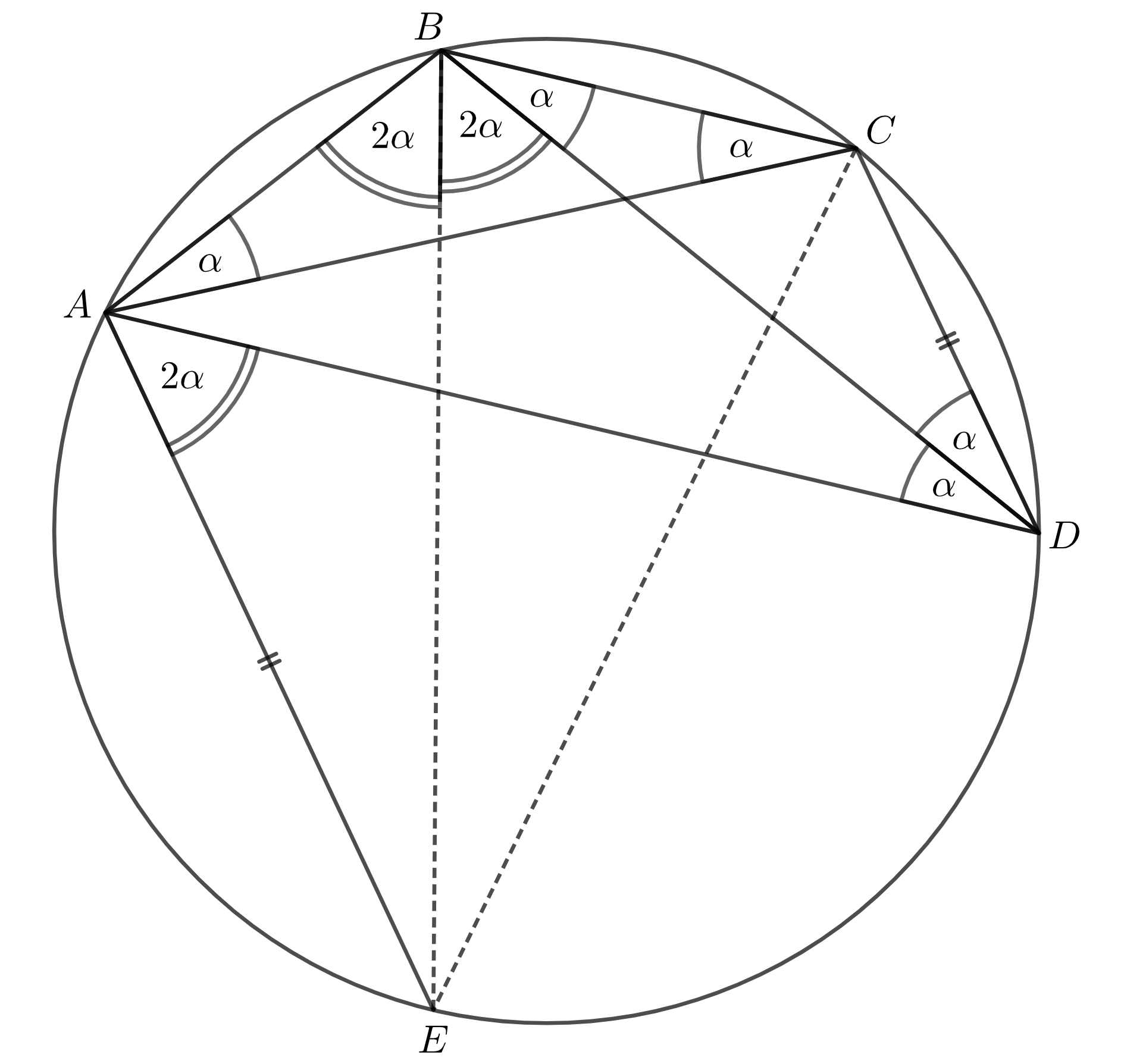
Ešte sme nevyužili rovnobežnosť \(CD\) a \(AE\). Všimnime si napríklad, že \(\sphericalangle EAD=\sphericalangle ADC\), keďže sú striedavé. Prenesieme si po kružnici ešte \(\sphericalangle BCA\ (=\alpha)\) do \(\sphericalangle BDA\) a zistíme, že \(\sphericalangle ADC = 2\alpha=\sphericalangle EAD\). Uhol \(\sphericalangle EAD\ ( = 2\alpha)\) potom vieme po kružnici preniesť do \(\sphericalangle EBD\ (=2\alpha)\). Vďaka tomu, že \(BE\) je os uhla \(ABD\) vieme, že \(\sphericalangle ABE = \sphericalangle EBD\ (= 2\alpha)\).

Teraz sa už len pozrieme na trojuholník \(ABC\), ktorého súčet vnútorných uhlov je \(180^\circ\). Pri základni máme dva razy \(\alpha\) a \(\sphericalangle ABC=5\alpha\). \(\sphericalangle ABC\) je teda \(\frac{5}{7}\cdot 180^\circ = \frac{900^\circ}{7}\).

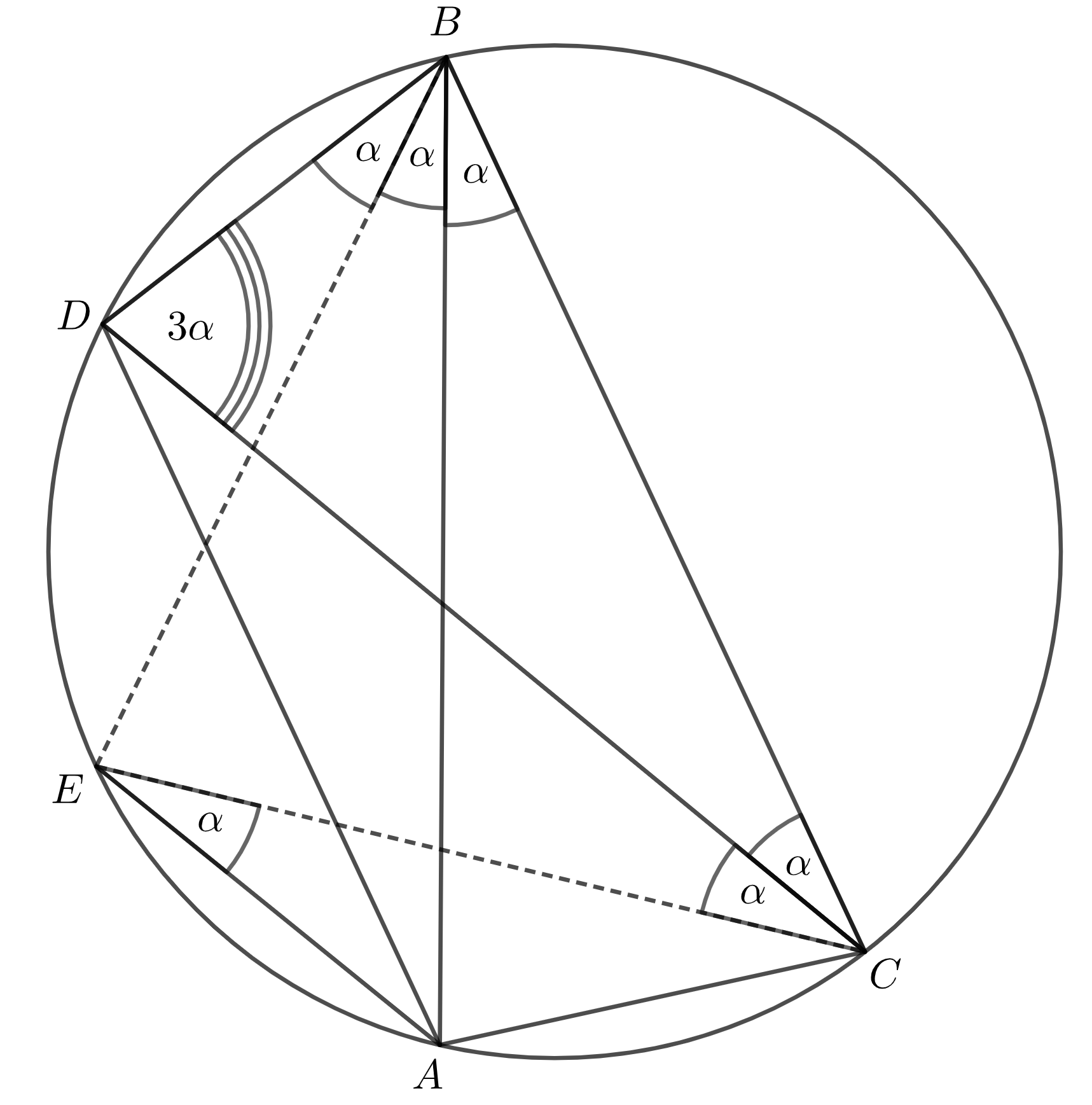
Teraz druhá konfigurácia. Tentokrát si v trojuholníkoch \(ABC\) a \(BCD\) pomenujeme \(\alpha\) uhol oproti základni, teda \(\sphericalangle BCD\) a \(\sphericalangle ABC\), ktorého hodnotu máme nájsť. Z obvodových uhlov vieme, že \(\sphericalangle ABC= \sphericalangle AEC\ (=\alpha)\). Následne opäť využijeme striedavé uhly: \(\sphericalangle AEC=\sphericalangle ECD\ (=\alpha)\) a nakoniec zase raz obvodové uhly \(\sphericalangle ECD = \sphericalangle DBE\ (=\alpha)\). Vďaka osi uhla \(BE\) vieme, že \(\sphericalangle DBE = \sphericalangle EBA\ (=\alpha)\). Keďže trojuholník \(DBC\) je rovnoramenný, uhly pri jeho základni sú rovnaké, teda \(\sphericalangle DBC=\sphericalangle BDC = 3 \alpha\).

A na záver, podobne ako v predošlej konfigurácií, sa pozrieme na trojuholník \(BCD\), v ktorom máme až \(7\alpha\), ktoré majú mať súčet \(180^\circ\). \(\sphericalangle ABC\) však má veľkosť len jedna \(\alpha\), a teda \(\sphericalangle ABC= \frac{180^\circ}{7}\).