3. Kradneme Mačku Sfingu $\left(\kappa \le 3\right)$ vzorové riešenie

Než sa pustíme do samotného riešenia, zamyslime sa nad tým, ako ovplyvňuje pozícia čísla v spodnom riadku hodnotu na vrchole pyramídy. Pri počítaní nasledujúceho riadku sa krajné čísla zarátajú vždy len v jednom políčku. Stredné políčka riadku majú naopak nad sebou \(2\) nové políčka, do ktorých sa zarátajú. Číslo, ktoré bolo v spodnom riadku na kraji sa teda zaráta iba raz. Políčko vedľa sa zaráta \(5\)-krát, a číslo z políčok uprostred sa zaráta až \(10\)-krát. To si koniec koncov môžeme všimnúť aj na obrázku 1.

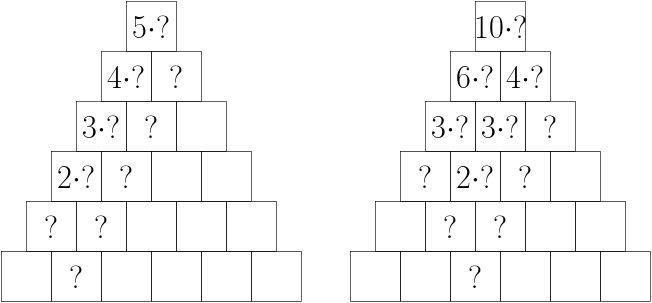
Prejdime k našej úlohe. Označme si \(x\) najmenšie číslo zo šestice v spodnom riadku. Ostatné čísla budú (v nejakom neznámom poradí) \(x+1,\, x+2,\, x+3,\, x+4,\, x+5\). Aby sme mohli počítať s umiestnením v spodnom riadku, povedzme, že číslo vľavo bude \(x+a\), vedľa neho \(x+b\), potom \(x+c,\, x+d,\, x+e\) až \(x+f\). Číslo na vrchu pyramídy tak môžeme napísať ako \[(x+a) + 5 \cdot (x+b) + 10 \cdot (x+c) + 10 \cdot (x+d) + 5 \cdot (x+e) + (x+f) = 32 x + a + 5 b + 10 c + 10 d + 5 e + f.\]

Vieme, že číslo na vrchu pyramídy je \(2022\). Dostaneme ho teda ako \(32\)-násobok najmenšieho čísla v spodnom riadku plus \(a + 5b + 10c + 10d + 5e + f\), pričom \(a, b, c, d, e, f\) sú navzájom rôzne celé čísla od \(0\) po \(5\). Na obmedzenie možných \(x\) nám pomôže zistiť, aké hodnoty môže mať \(a + 5b + 10c + 10d + 5e + f\). Keď najmenšie čísla vezmeme najmenej ráz a najväčšie najviac, dostaneme najväčší súčet, ktorý je \[0 + 5 \cdot 2 + 10 \cdot 4 + 10 \cdot 5 + 5 \cdot 3 + 1 = 116.\] Naopak, ak vezmeme najmenšie čísla najviackrát a najväčšie najmenejkrát, dostaneme najmenší súčet, ktorý má hodnotu \[5 + 5 \cdot 3 + 10 \cdot 1 + 10 \cdot 0 + 5 \cdot 2 + 4 = 44.\]

Takže \(32x\) bude medzi číslami \(1906 \,(=2022-116)\) a \(1978 \,(=2022-44)\). Jediné násobky \(32\) v tomto rozmedzí sú \(1920\) a \(1952\). Vidíme, že \(1920 : 32 = 60\) a \(2022 - 1920 = 102\) a \(1952 : 32 = 61\) a \(2022 - 1952 = 70\). Jediné možné vyhovujúce množiny čísel sú teda \(60\) až \(65\) s \(a + 5b + 10c + 10d + 5e + f = 102\) a \(61\) až \(66\) s \(a + 5b + 10c + 10d + 5e + f = 70\). Zadanie sa ale pýta na konkrétne poradia, preto musíme nájsť aj tie.

Všimnime si, že vymenením \(a, f\) neovplyvníme hodnotu súčtu \(a+5b+10c+10d+5e+f\), podobne ani vymenením \(b, e\) či \(c, d\). Preto môžeme predpokladať, že \(a<f, b<e, c<d\), pričom pre každé takéto riešenie sa môžeme rozhodnúť ľubovoľné dvojice prehodiť. To však znamená, že pre každú dvojicu máme \(2\) možnosti (prehodiť/neprehodiť) a dokopy je všetkých možných preusporiadaní preto \(2^3=8\).

Čísla 60 až 65

Vieme, že \(a+5b+10c+10d+5e+f=102\). To však znamená, že \(a+f\) dáva zvyšok \(2\) po delení piatimi. Keďže ale \(a, f\in\{0,1,2,3,4,5\}\) a taktiež \(a<f\), tak možné dvojice \((a,f)\) sú \((0, 2)\), \((2, 5)\), \((3, 4)\).

Pre dvojicu \((0,2)\) dostávame \(5b+10c+10d+5e=100\Leftrightarrow b+2c+2d+e=20\), a teda \(b+e\) musí byť párne, a teda \(b, e\) musia mať rovnakú paritu. Nakoľko nám však ostávajú už len čísla \(\{1,3,4,5\}\), možné dvojice \((b, e)\) sú \((1, 3)\), \((1, 5)\), \((3, 5)\). Z nich sú už \(c, d\) očividne jednoznačne určené. Hodnota súčtu \(b+2c+2d+e\) je pre tieto dvojice postupne \(22, 20, 18\), čiže vyhovuje len šestica \(60, 61, 63, 64, 65, 62\) a jej spomínané preusporiadania.

Pre zvyšné dve dvojice očividne platí \(a+f=7\), a preto \(5b+10c+10d+5e=95\Leftrightarrow b+2c+2d+e=19\). Vidíme teda, že \(b+e\) musí byť nepárne, čiže \(b, e\) musia mať rozličnú paritu.

Pri dvojici \((2, 5)\) nám ostávajú čísla \(\{0,1,3,4\}\), takže možné dvojice \((b, e)\) sú \((0, 1)\), \((0, 3)\), \((1, 4)\), \((3, 4)\). Pre ne súčet \(b+2c+2d+e\) nadobúda hodnoty \(15, 13, 11\) a \(9\), čiže pre túto dvojicu nemáme riešenie.

No a pri dvojici \((3, 4)\) máme ešte k dispozícii \(\{0, 1, 2, 5\}\), preto možné dvojice \((b, e)\) sú \((0, 1)\), \((0, 5)\), \((1, 2)\), \((2, 5)\) a im prislúchajúce súčty vychádzajú \(15, 11, 13, 9\), čiže ani tu ďalšie riešenia nenájdeme.

Čísla 61 až 66

Teraz má súčet \(a+5b+10c+10d+5e+f\) hodnotu \(70\). To však znamená, že \(b+e\) musí byť deliteľné piatimi. Možné dvojice \((a, f)\) sú teda \((0, 5)\), \((1, 4)\), \((2, 3)\). Všimnime si, že vo všetkých platí \(a+f=5\), čiže vieme vo všeobecnosti povedať, že \(5b+10c+10d+5e=65\Leftrightarrow b+2c+2d+e=13\), a teda \(b, e\) musia mať rozličnú paritu.

Začnime dvojicou \((0,5)\). Zostávajú nám čísla \(\{1, 2, 3, 4\}\), pre ktoré možné dvojice \((b, e)\) sú \((1, 2)\), \((1, 4)\), \((2, 3)\), \((3, 4)\) a im prislúchajúce súčty sú \(17, 15, 15, 13\). Vyhovuje teda šestica \(61, 64, 62, 63, 65, 66\).

Následne vezmime dvojicu \((1, 4)\). Pre zostávajúce čísla \(\{0,2,3,5\}\) sú možnými dvojicami \((b,e)\) dvojice \((0, 3)\), \((0, 5)\), \((2, 3)\), \((2, 5)\). Hodnoty \(b+2c+2d+e\) pre tieto dvojice sú \(17, 15, 15\) a \(13\), čiže v tejto vetve vyhovuje šestica \(62, 63, 61, 64, 66, 65\).

Nakoniec nám ostáva už len dvojica \((2, 3)\). Tentokrát vyberáme \(b, e\) z čísel \(\{0, 1, 4, 5\}\), čiže možné dvojice sú \((0, 1)\), \((0, 5)\), \((1, 4)\), \((4, 5)\). Im prislúchajú súčty \(19, 15, 15\) a \(11\), čiže tu sme ďalšie riešenie nenašli.

Riešeniami sú teda šestice \((60, 61, 63, 64, 65, 62)\), \((61, 64, 62, 63, 65, 66)\), \((62, 63, 61, 64, 66, 65)\) a ich permutácie, kde prehodíme prvé číslo so šiestym, druhé s piatym a/alebo tretie so štvrtým. Z každej z týchto možností teda vieme vyrobiť \(7\) ďalších (dokopy ich je \(2^3=8\)) a celkovo máme \(24\) možností.