9. Kradneme Modernú Skrinku vzorové riešenie

Pri mnohých kombinatorických úlohách je výhodné hľadať niečo, čo ostáva nemenné – tzv. invariantné. Poďme sa pokúsiť niečo podobné nájsť aj tu.

Označme \(R_n\) počet červených, \(G_n\) zelených a \(B_n\) modrých kameňov po \(n\) ťahoch od začiatku hry. Ak by žirafka v nejakom ťahu napríklad vybrala zo skrinky 3 modré kamene, tak by platilo \[R_{n+1}=R_n,\qquad G_{n+1}=G_n,\qquad B_{n+1}=B_n-3.\tag{1}\] Ak by naopak vymenila napríklad modrý a červený kameň za dva zelené, mali by sme \[R_{n+1}=R_n-1,\qquad G_{n+1}=G_n+2,\qquad B_{n+1}=B_n-1.\tag{2}\] Keď sa na rovnice lepšie zapozeráme, poprípade sa skúšame hrať s počtami kameňov a zisťovať, ako sa menia, vieme si všimnúť, že rozdiel \(R_n-G_n\) sa v každom ťahu môže znížiť o \(3\), nezmeniť alebo zvýšiť o \(3\). Konkrétne, z \((1)\) vidíme, že \(R_{n+1}-G_{n+1}=R_n-G_n\) a pre \((2)\) platí \(R_{n+1}-G_{n+1}=R_n-1-(G_n+2)=(R_n-G_n)-3\). Môžete si premyslieť, že podobne by to fungovalo, aj keby sme v \((1)\), \((2)\) zamenili farby. Uvidíte tak aj spôsob, akým môžeme \(R_n-G_n\) zvýšiť o tri – tak, že modrý a zelený kameň vymeníme za dva červené. Ďalej sa vieme pozrieť aj na rozdiely \(G_n-B_n\), \(B_n-R_n\). Jednotlivých kameňov je síce na začiatku hry rôzne veľa, no ťahy, ktoré s nimi môžeme robiť, sú v istom slova zmysle „symetrické“ – preto bude rovnaká vlastnosť platiť aj pre tieto dva rozdiely.

Dostali sme teda, že všetky tri rozdiely \(R_n-G_n, G_n-B_n, B_n-R_n\) sa v jednom ťahu môžu zmeniť o číslo z množiny \(\{-3, 0, 3\}\). To vieme interpretovať aj tak, že ich zvyšok po delení tromi zostáva po celú hru rovnaký. Ako sme si tým však pomohli? Zamyslime sa, ako by hra vyzerala vtedy, keď by napríklad Modrá žirafka po \(N\) krokoch vyhrala. Potom by nutne muselo platiť \(R_N=G_N=0\), a teda aj \(R_N-G_N=0\). My však vieme, že \(R_N-G_N\equiv R_0-G_0\pmod3\). Zároveň, \(R_0=31\), \(G_0=41\) (pretože počet kameňov po nula ťahoch je očividne počet kameňov na začiatku hry), a preto \(R_0-G_0\equiv-10\equiv2\pmod3\). Tu už ale začíname vetriť spor. Totiž, keďže \(R_0-G_0\equiv2\pmod3\), celú hru musí zvyšok rozdielu počtu červených a zelených kameňov ostať rovný dvom. Potom ale nie je možné, aby \(R_N-G_N\equiv0\pmod3\), a teda Modrá nevie vyhrať. Smutný príbeh…

Podobnú úvahu vieme urobiť aj pre Zelenú. Všimnime si, že \(B_0-R_0=59-31=28\equiv1\pmod3\), a teda ani Zelená vyhrať nevie. Keď sa však pozrieme na \(G_0-B_0=41-59=-18\equiv0\pmod3\), zisťujeme, že tu spor nedostaneme. To však ešte neznamená, že Červená má víťaznú stratégiu – len sa nám to zatiaľ nepodarilo vylúčiť. Poďme sa teda bližšie pozrieť na jej situáciu.

Odteraz budeme trojicou čísel označovať postupne počty červených, zelených a modrých kameňov v jednotlivom ťahu. Už sme si všimli, že v tejto úlohe sú zaujímavé zvyšky po delení tromi, budeme ich teda skúmať.

Počty kameňov v prvom ťahu sú \((31, 41, 59)=(3\cdot10+1, 3\cdot13+2, 3\cdot19+2)\). Prvým typom ťahu sa zvyšky po delení tromi očividne nezmenia. Tým druhým, keďže \(-1\equiv+2\pmod3\), sa všetky tri zvyšky znížia o \(1\) (poprípade sa ešte vedia zvýšiť o \(3\), keby mali ísť do záporných čísel). Tým si vieme zakresliť nasledovný pomerne jednoduchý graf prechodov medzi zvyškami.

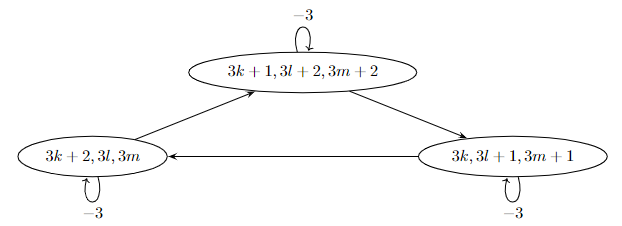
Teraz si môžeme uvedomiť nasledovnú vec – ak vieme, ktorá žirafka začínala, vieme, koľko kameňov je aktuálne v hre a vieme, aké sú ich zvyšky po delení tromi, vieme z toho jednoznačne určiť, ktorá žirafka je na ťahu. Totiž, keďže počet kameňov sa môže meniť len tak, že sa zníži o \(3\), vieme presne určiť, koľko ťahov prvého typu sa udialo. Zároveň, keďže zvyškové triedy kameňov sú v cykle dĺžky \(3\), vieme určiť, aký je zvyšok počtu týchto ťahov po delení tromi. Tým vieme určiť aj zvyšok počtu všetkých ťahov po delení tromi, z čoho už s využitím informácie o začínajúcej žirafke vieme určiť tú aktuálne na ťahu.

Vieme si uvedomiť, že toto platí aj obrátene – ak vieme počiatočnú žirafku, žirafku aktuálne na ťahu a počet kameňov, vieme z toho určiť zvyšky počtov kameňov po delení tromi.

Ďalej nám ešte môže pomôcť pozrieť sa, čo sa deje, keď už je kameňov v hre málo. Skúmajme, čo sa deje, keď máme najviac \(5\) kameňov. S využitím grafu 1 vieme, že možností na ich počty nie je až tak veľa. Zakreslime si šípkami možné pohyby ťahmi medzi nimi.

Počty \((5, 0, 0)\) a \((2, 0, 0)\) sú také, v ktorých Červená už podľa pravidiel vyhrala. Z počtu \((0, 1, 1)\) je možné urobiť len jeden ťah, a to taký, že sa dostaneme do \((2, 0, 0)\). Znamená to, že ak sa takéto počty kameňov vyskytnú v skrinke, je už nezvratné, že vyhrá Červená. Vyfarbime tieto stavy červenou a poďme zistiť, akým spôsobom sa dajú dosiahnuť.

Vyfarbime červenou aj všetky hrany, ktorými sa dá dostať do červených stavov. Ďalej si uvedomme, že keď je Červená v stave, z ktorého vedie červená hrana, použije ju a vyhrala. Vyfarbime preto takéto stavy svetločervenou.

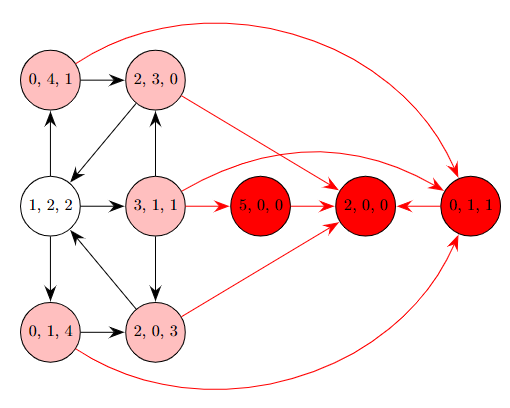
Všimnime si, že nám ostal jediný nezafarbený stav, a to \((1, 2, 2)\). To znamená, že ak sa žirafky dostanú na počet kameňov nanajvýš \(5\), jediný spôsob, akým môžu zvyšné dve vyhrať nad Červenou, je v každom ťahu ju dostať do \((1, 2, 2)\).

Teraz si však spomeňme, že z grafu 1 vieme na základe počiatočnej žirafky, žirafky aktuálne na ťahu a počtu kameňov určiť zvyšky kameňov po delení tromi.

Poďme teda preskúmať, čo sa deje, keď by začínali jednotlivé žirafky.

Ak by začínala Modrá, predpokladajme, že by sa Červená dostala na ťah, v ktorom by v skrinke zostávalo \(5\) kameňov. Keďže Červená ide hneď po Modrej, muselo doposiaľ ubehnúť \(3n+1\) ťahov pre nejaké \(n\in\mathbb N_0\). Z nich \(\frac13(31+41+59-5)=42\) sa využilo na znižovanie počtu kameňov, čiže zvyšnými \(3n-41=3(n-14)+1\) sa menili zvyšky kameňov. Potom ale z grafu 1 vidíme, že zvyšky kameňov na ťahu Červenej musia byť \((3k, 3l+1, 3m+1)\), čo jej umožňuje potiahnuť do víťaznej pozície.

Treba ešte ukázať vyššie uvedený predpoklad, a to, že sa vieme dostať do situácie, kedy je Červená na ťahu a v skrinke je päť kameňov. To je však očividné, lebo ak by ich bolo viac, na základe zvyškov ich musí byť aspoň \(8\), a potom už z Dirichletovho princípu existuje aspoň jedna farba, z ktorej sú aspoň tri kamene. To ale znamená, že Červená vie v každom ťahu, v ktorom je v skrinke viac ako 5 kameňov, odobrať tri kamene nejakej farby. Keďže však nevieme kamene pridávať, v najneskôr \(43.\) ťahu sa jej podarí, že bude mať na svojom ťahu 5 kameňov v skrinke.

Situácia je podobná, keď začína Zelená – Červená sa vie dostať do stavu, že na svojom ťahu je \(5\) kameňov v skrinke, dovtedy muselo ubehnúť \(3n+2\) ťahov, z ktorých \(42\) znižovalo počty kameňov, čiže \(3(n-14)+2\) menilo zvyšky. Preto zvyšky na ťahu Červenej sú \((3k+2, 3l, 3m)\), a teda sa vie dostať do víťaznej pozície.

Ešte ostáva prípad, kedy začína Červená. Ak by sme skúmali, s akými zvyškami bude pri piatich kameňoch, zistili by sme, že sú to zrovna neblahé \((3k+1, 3l+2, 3m+2)\). Tieto z grafu 2 očividne majú len jeden stav, a to \((1, 2, 2)\). Intuitívne to teda vyzerá tak, že Červená nevie vyhrať. Poďme teda ukázať, že zvyšné dve žirafky vedia Červenej prekaziť výhru.

Ak Červená odoberie tri kamene nejakej farby, Zelená aj Modrá odoberú tiež tri kamene nejakej farby. No a pokiaľ Červená vymení kamene dvoch rôznych farieb za dva kamene tretej farby, Zelená a Modrá urobia analogický ťah pre zvyšné dve farby.

Je očividné, že keď vie odobrať tri kamene Červená, vedia ich odobrať aj Zelená a Modrá. To platí, lebo vždy odoberajú po deviatich a \(31+41+59=9\cdot14+5\), pričom keď má Červená \(5\) kameňov, musí ich mať v počtoch \((1, 2, 2)\), a teda nevie ďalšie tri odobrať. Zároveň, ak je na stole viac ako \(5\) kameňov (čo je vzhľadom na zvyšky aspoň \(8\)), tak z Dirichletovho princípu sú na nejakej kôpke aspoň tri z nich, teda Modrá a Zelená odoberať vedia.

Očividne má Červená na začiatku svojho ťahu aspoň jeden červený kameň, aspoň dva zelené a aspoň dva modré. Ak teda vymení

• červený a zelený za dva modré, Zelená môže vymeniť zelený a modrý za dva červené a Modrá červený a modrý za dva zelené,

• červený a modrý za dva zelené, Zelená môže vymeniť zelený a modrý za dva červené a Modrá červený a zelený za dva modré,

• zelený a modrý za dva červené, Zelená môže vymeniť červený a modrý za dva zelené a Modrá červený a zelený za dva modré.

Dostali sme teda, že Zelená a Modrá skutočne vedia svoje ťahy uskutočniť, a teda neumožnia Červenej vyhrať. To však znamená, že ak Červená nezačína, tak má víťaznú stratégiu, inak víťaznú stratégiu nemá nikto.