2. Koncept Monumentálnej Strechy $\left(\kappa \le 2\right)$ vzorové riešenie

Na začiatok sa nám určite zíde náčrt. Už zo zadania si toho vieme celkom dosť zakresliť, avšak v náčrte sú už aj niektoré čiary a body, ktoré nám budú nápomocné neskôr. Taktiež si označíme priesečník úsečiek \(TZ\) a \(MS\) ako \(S'\), a priesečník polpriamky \(ZT\) a úsečky \(KM\) ako \(K'\).

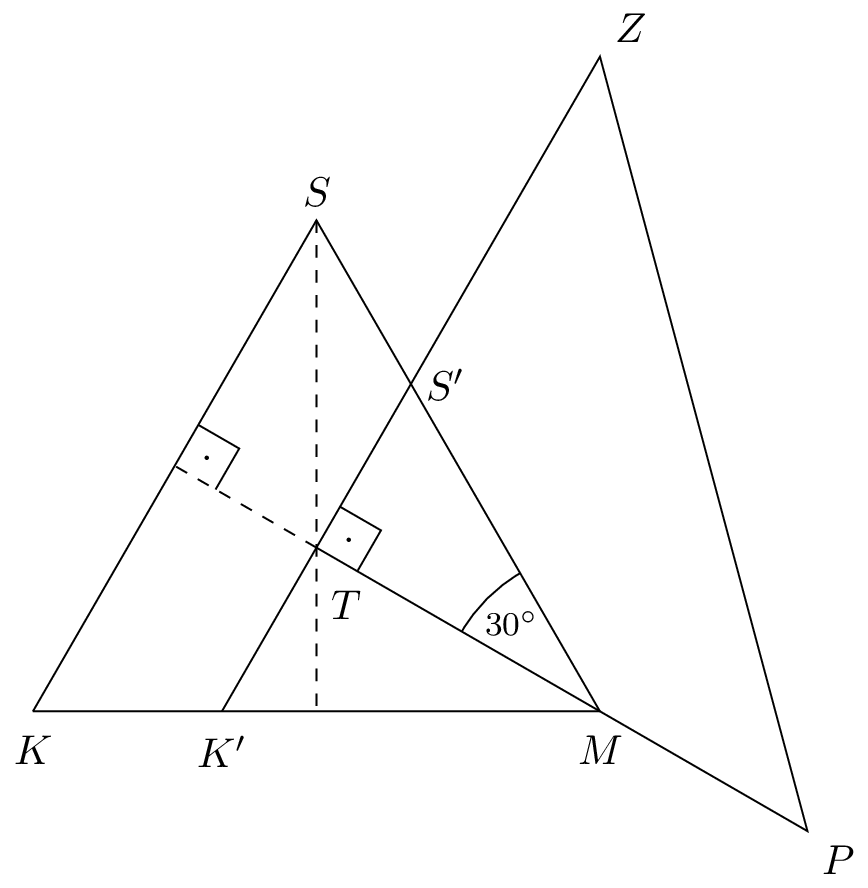
Zamyslime sa nad tým, ako by sme mohli dospieť k výsledku. Obsah trojuholníka \(TPZ\) už vieme prakticky zo zadania, nakoľko poznáme dĺžky jeho odvesien, ktoré sú v pravom uhle. Ak by sme boli schopní vypočítať obsah trojuholníka \(TMS'\), vieme obsah štvoruholníka \(MPZS'\) a výsledný pomer dostať jednoducho.

Veľmi nápomocné nám budú v tejto úlohe vedomosti o ťažniciach v rovnostrannom trojuholníku. Vieme, že ťažnice sú zároveň aj výšky, teda sú kolmé na strany, a tak ako v každom trojuholníku, ťažisko vždy rozdeľuje ťažnice v pomere \(2:1\). Ak si označíme dĺžku strany \(KM\) ako \(a\), potom pomocou Pytagorovej vety vieme vypočítať dĺžku ťažnice ako

\[\begin{align} \left(\frac a2\right)^2 + t^2 &= a^2,\\ t^2 &= a^2 - \left(\frac {a^2}{4}\right),\\ t &= \sqrt{\frac{3a^2}{4}},\\ t &= \frac{\sqrt3}{2}a.\end{align}\]

No a kedže dĺžka celej ťažnice je \(\frac{\sqrt3}{2}a\), dĺžka úsečky \(TM\) musí byť \[\frac23 \cdot \frac{\sqrt3}{2}a = \frac{\sqrt3}{3}a.\]

Ostáva nám zistiť už len dĺžku úsečky \(TS'\). Jedným zo spôsobov, ako ju nájsť, je uvedomiť si podobnosť trojuholníkov \(KMS\) a \(K'MS'\), ktoré sú podobné, lebo zdieľajú uhol pri vrchole \(M\), a uhly pri vrcholoch \(K\) a \(K'\), resp. \(S\) a \(S'\) sú súhlasné. Nakoľko už poznáme, že dĺžka \(TM\) sú \(\frac 23\) z dĺžky ťažnice, vieme určiť aj koeficient podobnosti týchto trojuholníkov, ktorý tým pádom musí taktiež byť \(\frac 23\). Pri podobných trojuholníkoch platí, že všetky korešpondujúce dĺžky v týchto trojuholníkoch sú zmenšené/zväčšené v tom istom pomere, a preto je dĺžka úsečky \(K'S'\) rovná \(\frac 23 a\). Nakoľko sa bod \(T\) nachádza v strede \(K'S'\), dĺžka úsečky \(TS'\) je \(\frac 13 a\). Túto dĺžku vieme dostať aj pomocou tangensu, ak si uvedomíme, že uhol \(S'MT\) má \(30^\circ\) (polovica z uhlu v rovnostrannom trojuholníku), potom dĺžku \(TS'\) vieme dostať ako \(|TS'| = \tan (30^\circ) \cdot |TM| = \frac{1}{\sqrt 3} \cdot \frac{\sqrt 3}{3}a = \frac 13 a\).

Ďalej potrebujeme zistiť jednotlivé obsahy trojuholníkov \(TPZ\) a \(TMS'\), a obsah štvoruholníka \(MPZS'\)

\[\begin{align} S_{TPZ} = \frac{a \cdot a}{2} &= \frac{a^2}{2},\\ S_{TMS'} = \frac{\frac{\sqrt3}{3}a \cdot \frac 13 a}{2} &= \frac{\sqrt 3}{18}a^2,\\ S_{MPZS'} = S_{TPZ} - S_{TMS'} = \frac{a^2}{2} - \frac{\sqrt 3}{18}a^2 &= \frac{9-\sqrt 3}{18}a^2.\end{align}\]

No a na záver zostáva už iba samotný pomer \(TMS'\) a \(MPZS'\), ktorý je

\[\begin{align} \frac{S_{TMS'}} {S_{MPZS'}} &= \frac{\frac{\sqrt 3}{18}a^2} {\frac{9-\sqrt 3}{18}a^2} = \frac{\sqrt 3}{9 - \sqrt 3} = \frac{\sqrt 3}{9 - \sqrt 3} \cdot \frac{9 + \sqrt 3}{9 + \sqrt 3} = \\ &= \frac{9\sqrt 3 + 3}{78} = \frac{3\sqrt 3 + 1}{26} \approx 0,238,\end{align}\]

kde sme použili usmernenie zlomku na odstránenie odmocniny z menovateľa. Výsledný pomer je teda v exaktnom tvare \(\frac{3\sqrt 3 + 1}{26}\), čo je približne \(0,238\).

Alternatívne konfigurácie

Zo zadania nie je jasne dané, kde presne sa má nachádzať bod \(Z\). V riešení sme ho umiestnili na polpriamku \(TS'\), no mohli sme ho kľudne dať aj na polpriamku \(TK'\). Avšak vďaka tomu, že trojuholník \(KMS\) je rovnostranný, máme v ňom symetriu okolo priamky \(TM\), a teda bez ohľadu na to, na ktorú stranu priamky \(TM\) umiestnime bod \(Z\), výsledok bude rovnaký.

Takisto by sme sa mohli zamýšľať nad polohou bodov \(P\) a \(Z\). Ako si môžeme byť istí, že sa tieto body nachádzajú mimo trojuholníka \(KMS\)? V tejto úlohe je to celkom jednoduché odôvodniť a nestrhávali sme body za to, keď ste to do riešenia neuviedli, no je to niečo, na čo sa vo všeobecnosti oplatí dávať pozor, nakoľko pri komplikovanejších úlohách to môže značne ovplyvniť výsledok alebo počet možných riešení.