9. Kolaudačka, Miestami Sranda vzorové riešenie

Najprv spomeňme prípad, kedy \(D = B\). Vtedy je daná dotyčnica spoločná pre obe kružnice, a tak \(E = F = B\), kedy platí \(|EF| = 0 = |DE|\). Ďalej sa už budeme zaoberať iba prípadom, kedy \(D \neq B\).

Začnime s analýzou výslednej situácie. Z tej sa dozvieme, čo od bodov očakávame, a teda aj ako ich nájdeme/zostrojíme.

Ako prvé označme \(b\) spoločnú dotyčnicu \(k,\, l\) prechádzajúcu bodom \(B\) a označme \(X\) jej priesečník s priamkou \(DE\). Ak sa nám podarí nájsť bod \(X\), ľahko z neho zostrojíme dotyčnicu k \(l\), aby sme našli \(D\).

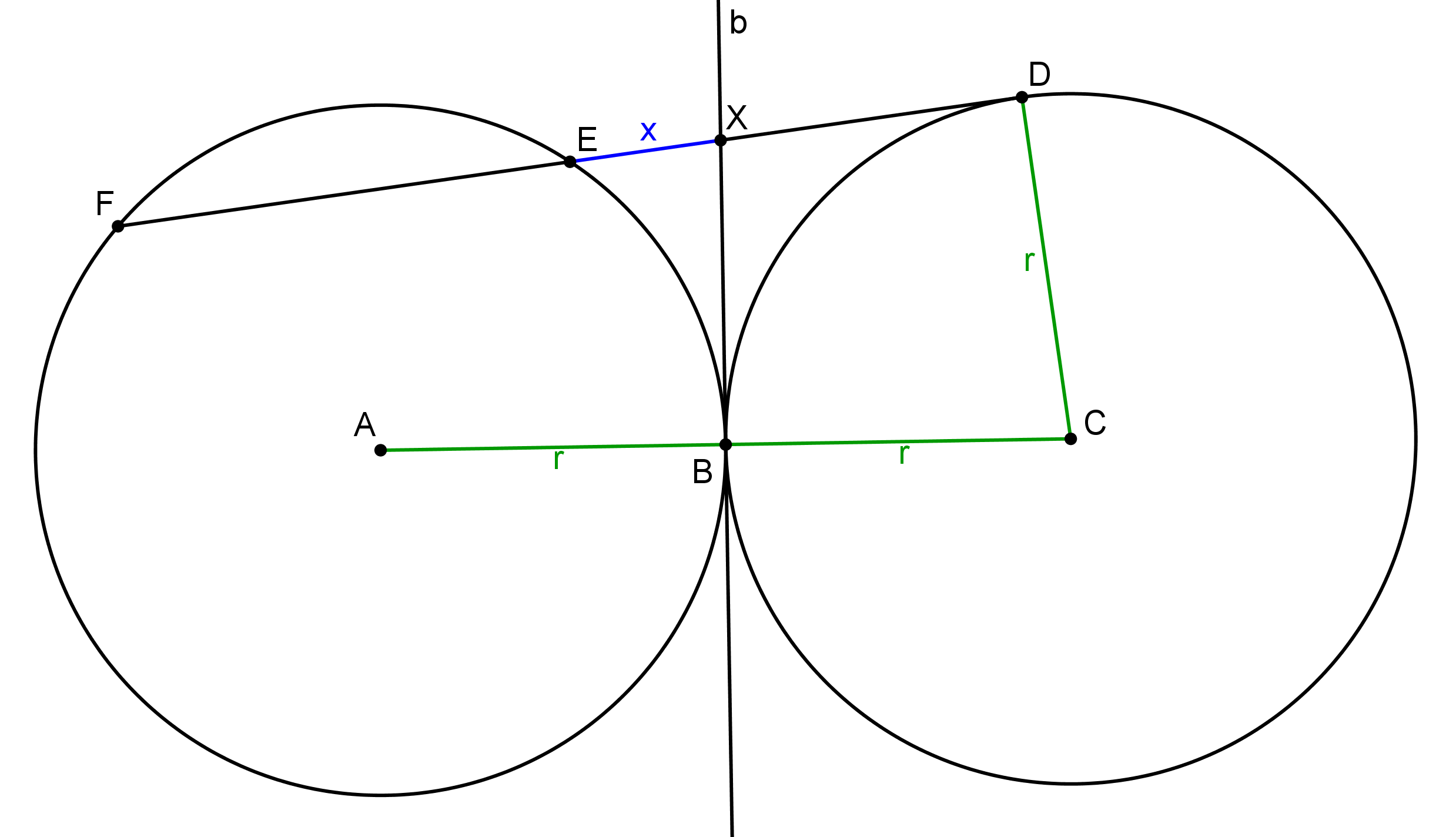
Skúsme teda zistiť niečo viac o bode \(X\). Vieme, že \(XB\) aj \(XD\) sú dotyčnice ku kružnici \(l\), takže úsečky \(XB\) a \(XD\) sú rovnako dlhé. Keď označíme \(|DE| = |EF| = d\) a \(|EX| = x\), dostaneme \(|XB| = |XD| = d - x\). Teraz sa zameriame na kružnicu \(k\) a využijeme mocnosť bodu \(X\). Bod \(B\) je bod dotyku a \(E, F\) sú priesečníky \(k\) s priamkou \(XD\). Platí teda \(|XB|^2 = |XE| \cdot |XF|\). Vyjadrenie pomocou \(x\) a \(d\) dáva rovnicu \[\begin{align} (d - x)^2 &= x \cdot (d + x),\\ d^2 - 2dx + x^2 &= dx + x^2,\end{align}\] odkiaľ ľahko dopočítame \(d = 3x\). (Alebo \(d = 0\), čo by opäť viedlo na prípad \(D = B\).)

Vidíme, že \(X\) sa nachádza v tretine úsečky \(ED\), no to nám nepomáha, keďže ani body \(E\) a \(D\) na začiatku nepoznáme. Priamku \(b\) zostrojiť vieme, no potrebovali by sme skôr vzdialenosť od niektorého z bodov \(A, B, C\). Tu sa nám zíde pozorovanie, že trojuholník \(ACX\) je rovnoramenný so základňou \(AC\). Priamka \(b\) je ako dotyčnica kolmá na \(AB\) aj \(BC\). Navyše \(|AB| = |BC| = r\) podľa zadania, takže bod \(X\) leží na osi \(AC\).

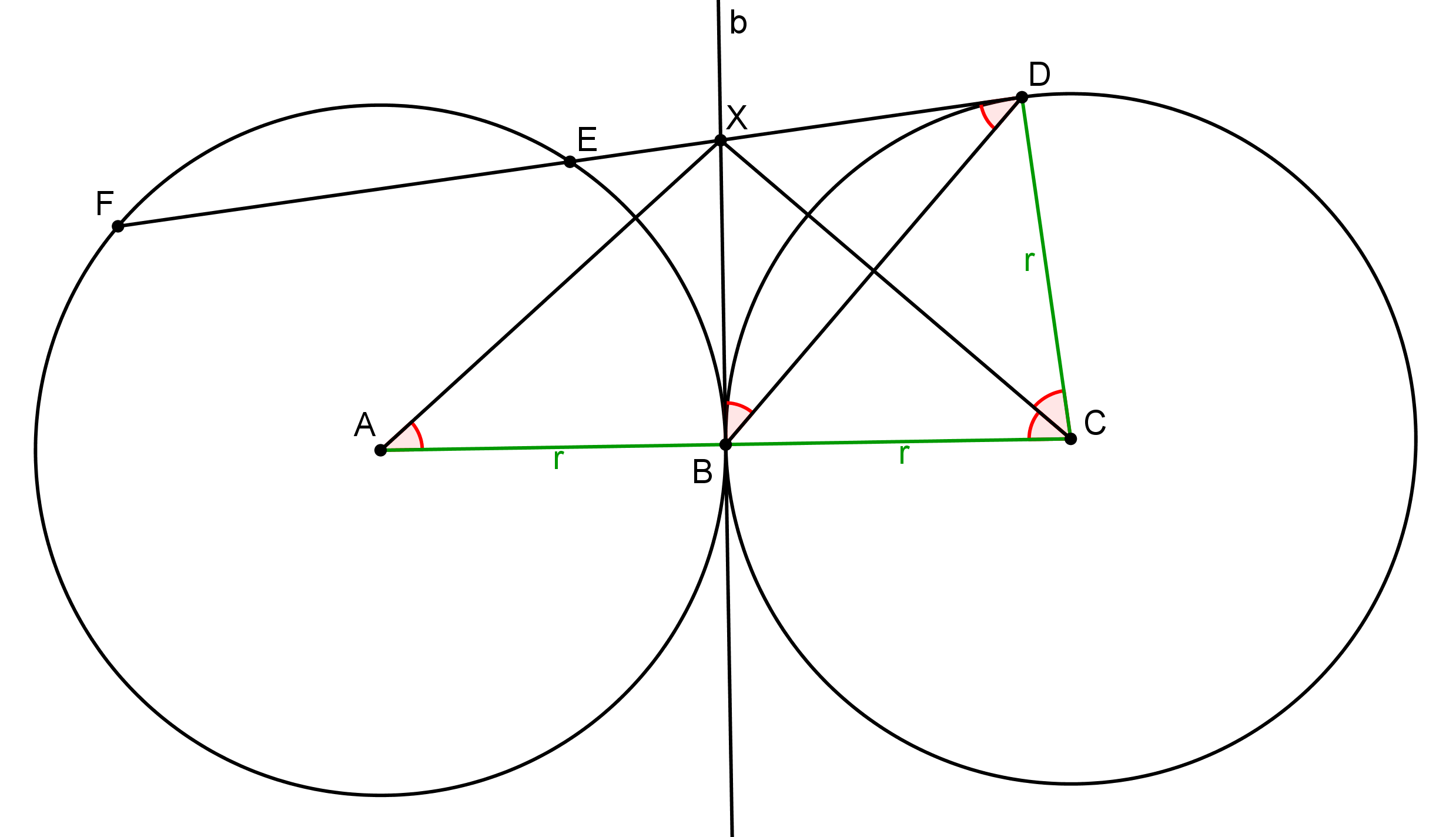
Označme \(\alpha = |\sphericalangle ACX| = |\sphericalangle CAX|\). Keďže \(|XB| = |XD| = 2x,\, |CB| = |CD| = r\) a úsečka \(CX\) je spoločná pre trojuholníky \(BCX\) a \(DCX\), sú tieto trojuholníky zhodné. Takže platí \(|\sphericalangle DCX| = \alpha\). Navyše sú spomínané trojuholníky pravouhlé, s pravým uhlom pri vrchole \(B\), resp. \(D\). Vďaka Tálesovej vete vieme, že body \(B, C, D, X\) ležia na kružnici. Veta o obvodových uhloch nám dáva \[|\sphericalangle XDB| = |\sphericalangle XCB| = \alpha = |\sphericalangle XCD| = |\sphericalangle XBD|.\] Trojuholník \(BDX\) je teda rovnoramenný so základňou \(DB\). Pri základni má navyše uhol \(\alpha\), rovnako ako trojuholník \(ACX\). Tieto trojuhoníky sú teda podobné podľa vety uu.

Vieme, že \(|AC| = 2r,\, |XB| = |XD| = 2x\). My z týchto dĺžok poznáme len polomer kružníc \(r\), chceli by sme však dostať \(x\), alebo aspoň \(|AX|\). Potom by sme vedeli zostrojiť bod \(X\) a následne by sme našli aj \(D\). Potrebujeme teda zistiť niečo viac o pomeroch strán v týchto podobných trojuholníkoch.

Využime teraz fakt, že \(B\) je stredom súmernosti kružníc \(k\) a \(l\). Ak \(A\), stred kružnice \(k\), zobrazíme v tejto stredovej súmernosti, dostaneme bod \(C\). Na zobrazenie celej kružnice \(k\) nám stačí zo stredu \(C\) spraviť kružnicu s rovnakým polomerom. To je práve kružnica \(l\). Vo všeobecnosti, ak máme dve dotýkajúce sa kružnice, ich bod dotyku bude stredom rovnoľahlosti týchto dvoch kružníc. Tento fakt sa Vám môže zísť aj v iných úlohách. Keďže \(k\) a \(l\) sú zhodné, miesto rovnoľahlosti dostaneme stredovú súmernosť.

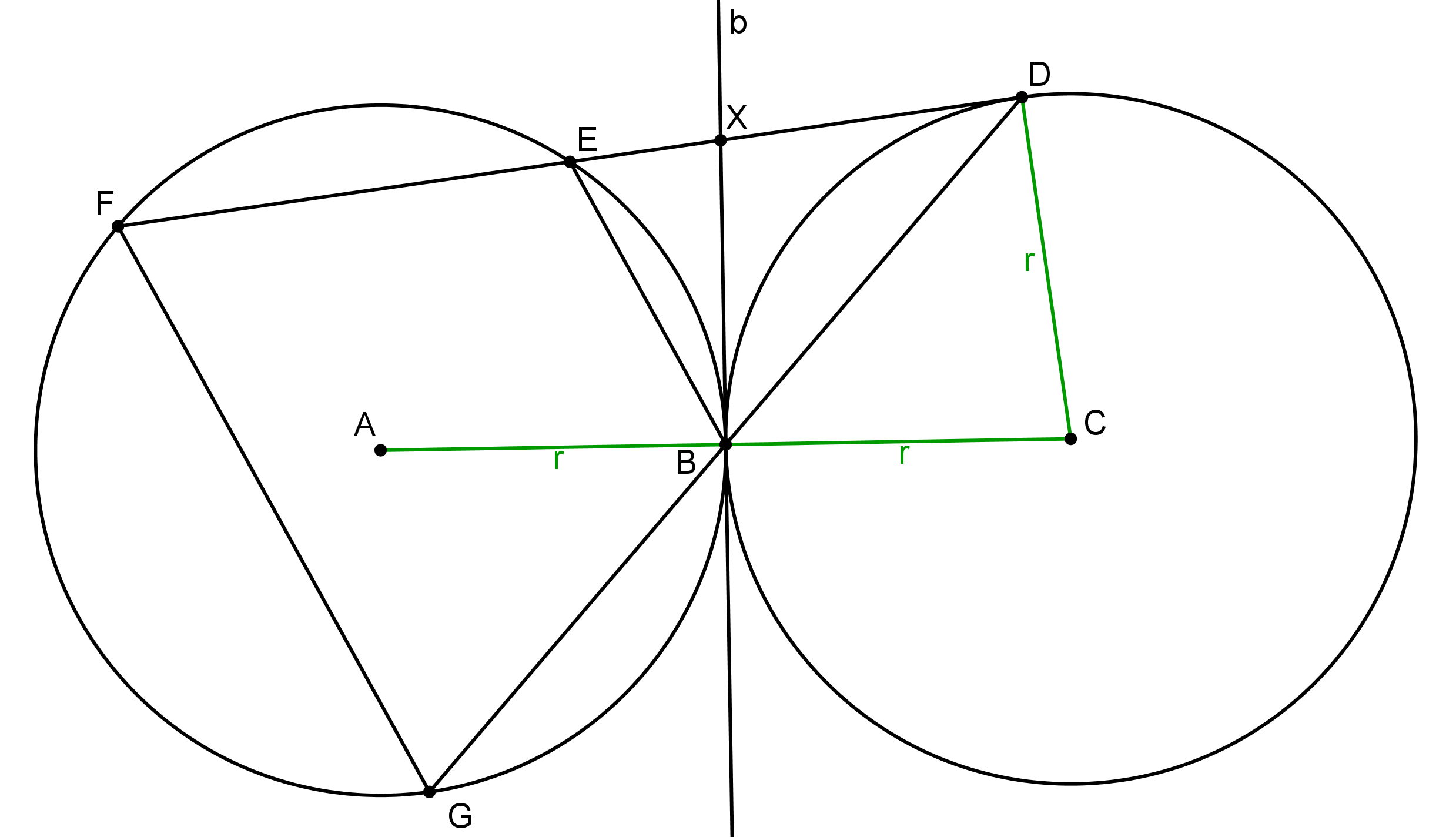
Predĺžme teraz úsečku \(BD\) na priamku a označme \(G\) jej druhý priesečník s \(k\). Vďaka stredovej súmernosti platí \(|BG| = |BD|\). V trojuholníku \(FGD\) je tak úsečka \(EB\) strednou priečkou. Takže je rovnobežná so základňou \(FG\). Štvoruholník \(FGBE\) je teda tetivový lichobežník a taký lichobežník musí byť rovnoramenný. (Vieme využiť napríklad fakt, že protiľahlé uhly v tetivovom štvoruholníku majú súčet \(180^\circ\).)

Zisťujeme teda, že \(|BG| = |EF| = 3x\). To znamená, že aj \(|BD| = 3x\). V trojuholníku \(BDX\) je teda pomer ramena ku základni \(2x : 3x = 2:3\) a ten musí byť rovnaký ako v trojuholníku \(ACX\). Platí teda \[|AX| = \frac{2}{3} |AC| = \frac{2}{3} \cdot 2r = \frac{4}{3} r.\]

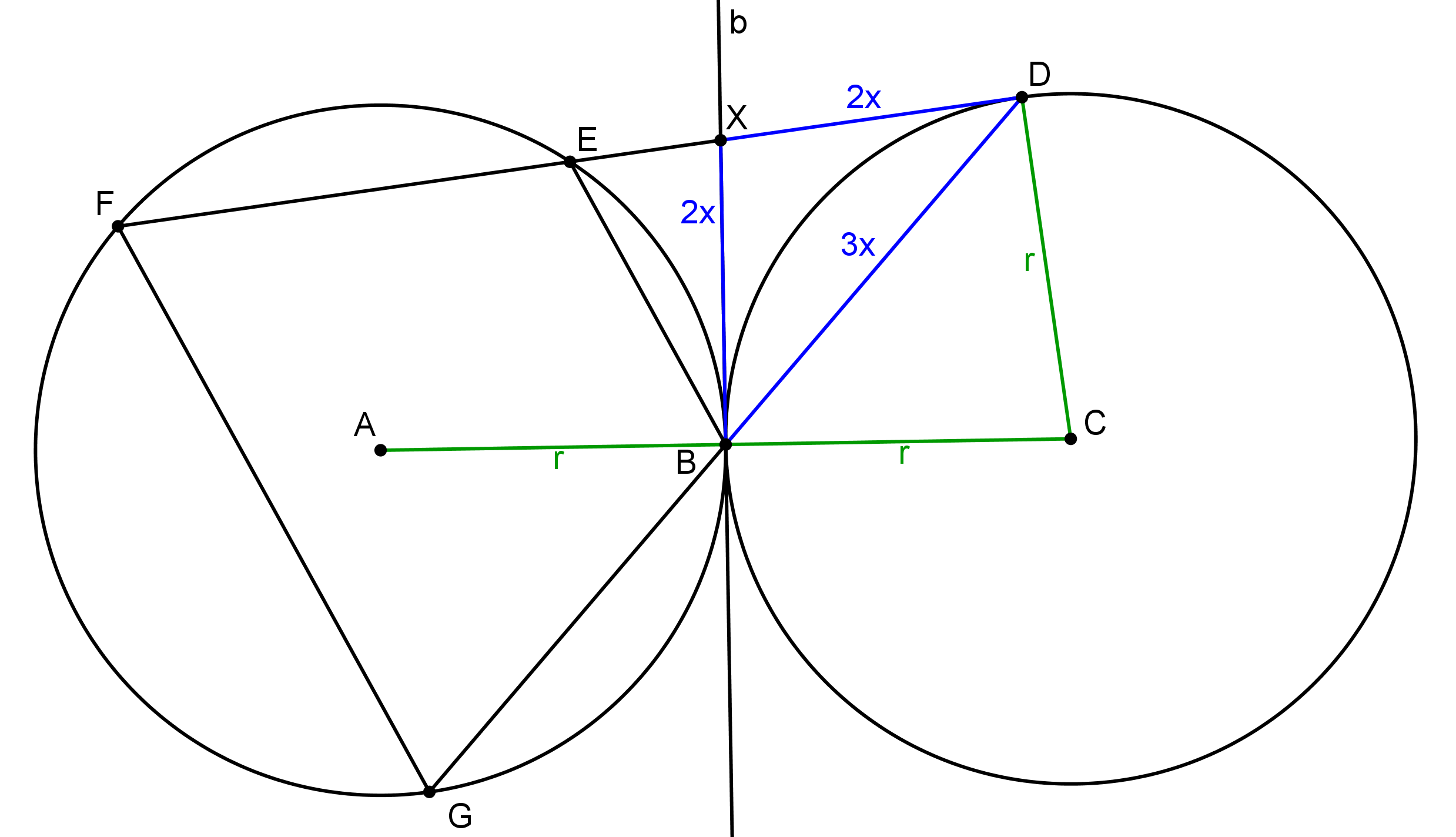
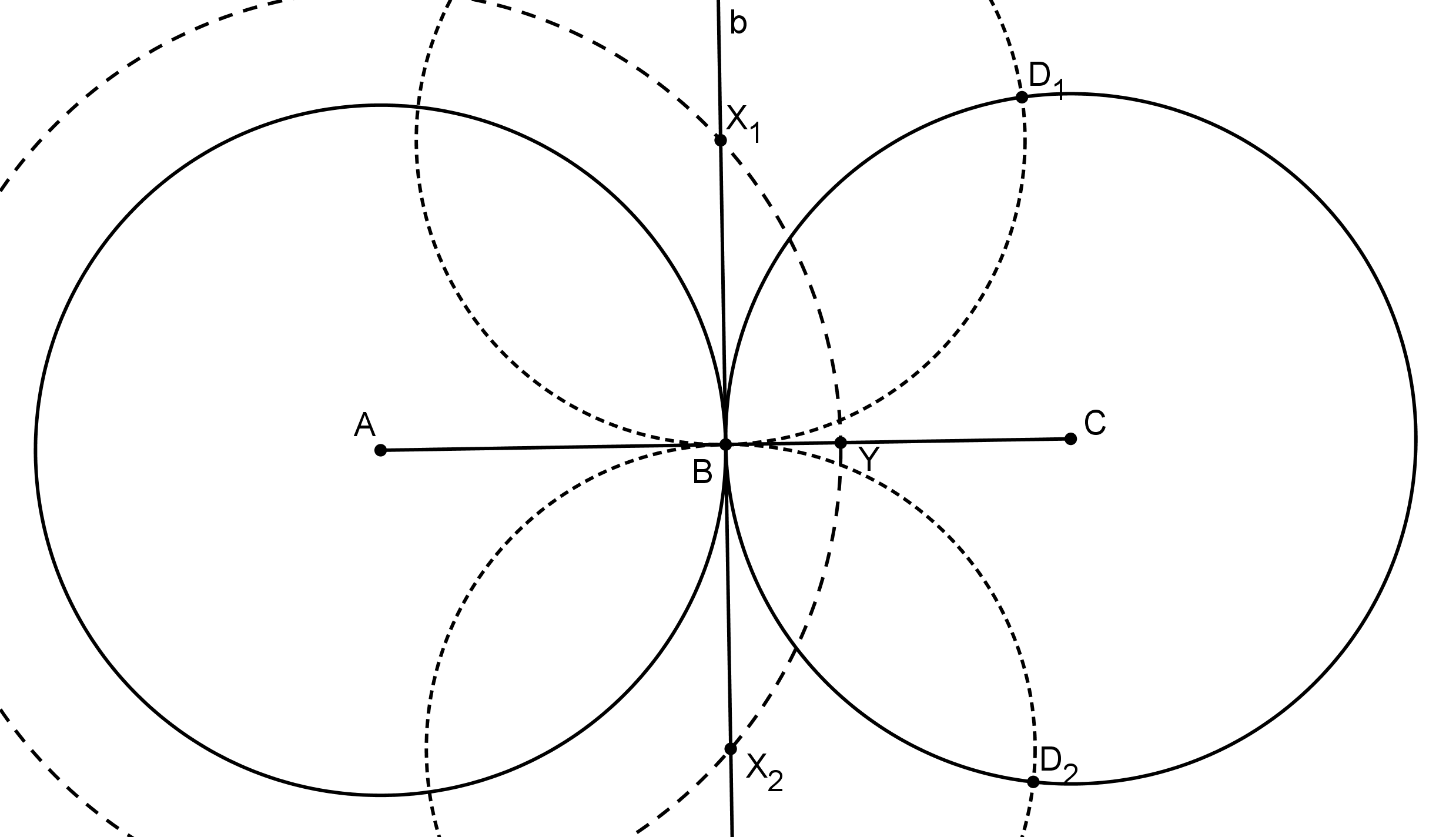
Teraz už vieme nájsť bod \(X\), a teda aj \(D\). Najprv zostrojíme priamku \(b\) – os úsečky \(AC\). Následne úsečku \(BC\) s dĺžkou \(r\) rozdelíme na tretiny¹, čím dostaneme nejaký bod \(Y\), pre ktorý \(|AY| = \frac{4}{3}r\). Kružnica so stredom v bode \(A\) a polomerom \(AY\) pretne \(b\) v dvoch bodoch, čo sú dve možnosti pre bod \(X\) – \(X_1\) a \(X_2\). Keďže \(|XB| = |XD|\), stačí nám spraviť kružnice so stredmi v \(X_1, X_2\) a polomermi \(X_1B, X_2B\) a dostaneme dve možné pozície bodu \(D\).