Zadanie
Krtko sa nachádzal v konzervatívnom poli, v ktorom sa prechádzal po svojich obľúbených chodníčkoch. Po chvíli zastal a uvedomil si, že práca, ktorú pole vykonalo, je nulová. Po bližšej analýze svojej trasy zistil, že je to preto, že išiel po obvode kosoštvorca.
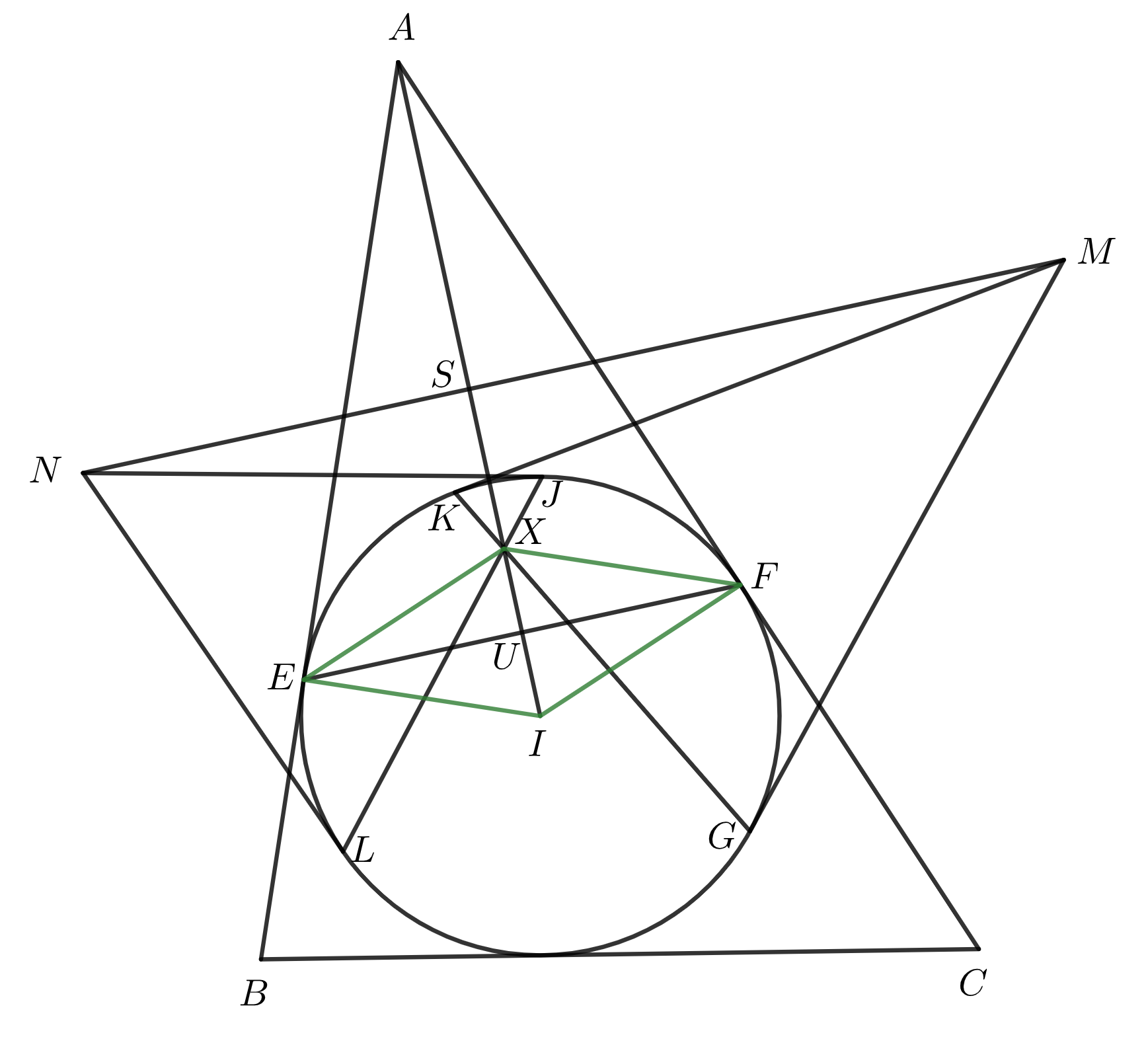
Majme trojuholník \(ABC\). Jeho vpísaná kružnica so stredom \(I\) sa dotýka strán \(AB\) a \(AC\) postupne v bodoch \(E\), \(F\). Označme \(M\) a \(N\) postupne ťažiská kružníc opísaných trojuholníkom \(AIC\) a \(AIB\). Veďme z bodu \(M\) dotyčnice ku kružnici vpísanej trojuholníka \(ABC\), ktoré sa jej dotýkajú v bodoch \(K\), \(G\). Analogicky veďme aj z bodu \(N\), ktoré sa dotýkajú zas v bodoch \(J\), \(L\). Priamky \(KG\) a \(JL\) sa pretínajú v bode \(X\). Dokážte, že \(EFXI\) je kosoštvorec.
Na začiatok si uvedomme, že \(I\) ako stred kružnice vpísanej trojuholníku \(ABC\) leží na osi úsečky \(EF\). Ak si jeho obraz v osovej súmernosti podľa \(EF\) označíme ako \(I'\), bude platiť, že \(II'\) a \(EF\) sú na seba kolmé a polia sa, teda tvoria kosoštvorec. Stačí teda dokázať, že body \(I\) a \(X\) sú osovo súmerné podľa priamky \(EF\).
Ďalej si všimneme, že priamka \(MN\) je z definície stredov opísaných kružníc osou úsečky \(AI\). Označme si teda stred \(AI\) ako \(S\). Následne označme \(U\) stred \(EF\). Nahliadneme, že body \(A\),\(S\),\(I'\), \(U\) a \(I\) ležia na priamke \(AI\). Následne je rovnako ľahko vidieť, že \(EAFI\) je tetivový deltoid.
Bystré oko geometra už tuší, že nám stačí len dokázať, že priamka \(MN\) je polárou1 bodu \(I'\) vzhľadom ku kružnici vpísanej, z čoho už z La Hire Theorem vyplýva, že body \(I'\) a \(X\) sú jeden a ten istý bod a tým vyhráme. To vyplýva z toho, že priamka, na ktorej ležia body dotyku dotyčníc vedených z jedného bodu, je polárou tohto bodu. Dá sa to nahliadnuť tým, že kolmý priemet bodu na túto priamku je práve jeho obraz v kružnicovej inverzii. To je presne prípad priamky \(KG\) a bodu \(M\) a \(LJ\) a \(N\).
Využijeme teraz fakt, že pre pól \(P\) a jeho priemet \(P'\) na jeho poláru platí, že \[|OP|\cdot|OP'|=r^2,\] kde \(O\) a \(r\) sú stred a polomer kružnice, vzhľadom ku ktorej je polára určená. V našom prípade \(P\), \(P'\) a \(O\) sú postupne \(I'\), \(S\) a \(I\). Teda chceme dokázať, že \[|I'I|\cdot|IS|=r^2=|IE|^2=|IF|^2.\] To sa podobá na nejakú mocnosť bodu \(I\) k vhodnej kružnici, pre ktorú platí, že jedna z priamok \(IE\) alebo \(IF\) je k nej dotyčnicou. Teraz už len nájsť takúto kružnicu. Ľahko si z tetivovosti \(AEIF\) vieme napísať nasledovnú rovnosť uhlov \[|\sphericalangle{UAE}|=|\sphericalangle{IAF}|=|\sphericalangle{IEF}|,\] čo znamená, že podľa vety o úsekovom uhle je priamka \(IE\) dotyčnicou ku kružnici opísanej trojuholníku \(AUE\). Mocnosť bodu \(I\) k tejto kružnici teda je \[|IE|^2=|IA|\cdot|IU|=\frac{1}{2}\cdot|II'|\cdot2\cdot|IS|=|I'I|\cdot|IS|,\] čo je presne to, čo sme chceli teda dokázať. Teda os \(AI\) je polárou bodu \(I'\), teda body \(X\) a \(I'\) sú ten istý bod a z toho vieme, že \(EXFI\) je kosoštvorec, čím je dôkaz hotový.
Ak si o polárach v živote nepočul, môžeš sa o nich dočítať napríklad v nasledovnom materiáli https://prase.cz/library/iKS-DvoupomeraPolaryPT/iKS-DvoupomeraPolaryPT.pdf↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.