Zadanie
Konštantín s Metodom na Veľkej Morave učili, učili, učili, až vyučili armádu učňov. Aby však mohli túto armádu použiť, museli ich nechať najprv vysvätiť. Vybrali sa teda do Ríma za pápežom Mikulášom I. Keď do Ríma dorazili, čakalo ich nepekné prekvapenie. Do cesty sa im postavili trojjazyčníci.
Trojjazyčník je hrozná potvora s troma jazykmi, ktoré sú označené \(H, G, L\)1 a tvoria trojuholník. Na strane \(HG\) sa nachádza bod \(S\)2, pričom platí, že kružnice vpísané trojuholníkom \(HLS\) a \(GLS\) sa dotýkajú úsečky \(LS\) v rovnakom bode. Dokážte, že bod \(S\) je bodom dotyku vpísanej kružnice trojuholníka \(HGL\) so stranou \(HG\).
Označme dotykové body kružníc s trojuholníkmi ako na obrázku nižšie.
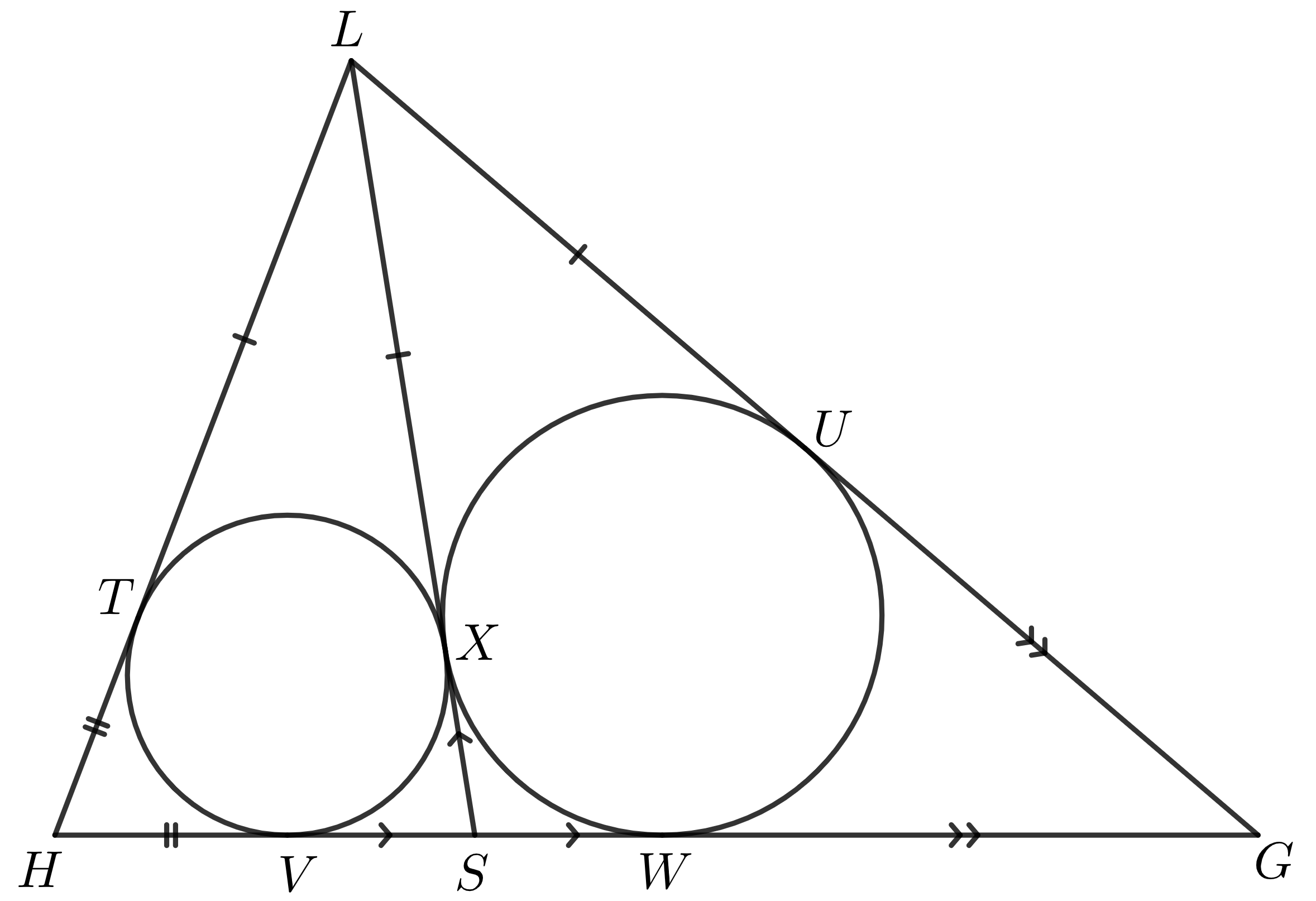
Pokiaľ z bodu vedieme dotyčnice ku kružnici, zo symetrie vyplýva, že vzdialenosť dotykových bodov od tohto bodu je rovnaká. Z toho máme, že \(|HT|=|HV|\), \(|LT|=|LX|\), \(|LU|=|LX|\), \(|GU|=|GW|\), \(|SV|=|SX|\) a \(|SW|=|SX|\).
Z predošlého odseku je zrejmé, že aby body \(A', B', C'\) ležiace postupne na stranách \(BC, CA, AB\) trojuholníka \(ABC\) mohli byť dotykovými bodmi kružnice vpísanej, musí platiť, že \(|AB'|=|AC'|\), \(|BA'|=|BC'|\) a \(|CA'|=|CB'|\). Ukážeme však, že táto podmienka nie je iba nutná, ale aj postačujúca.
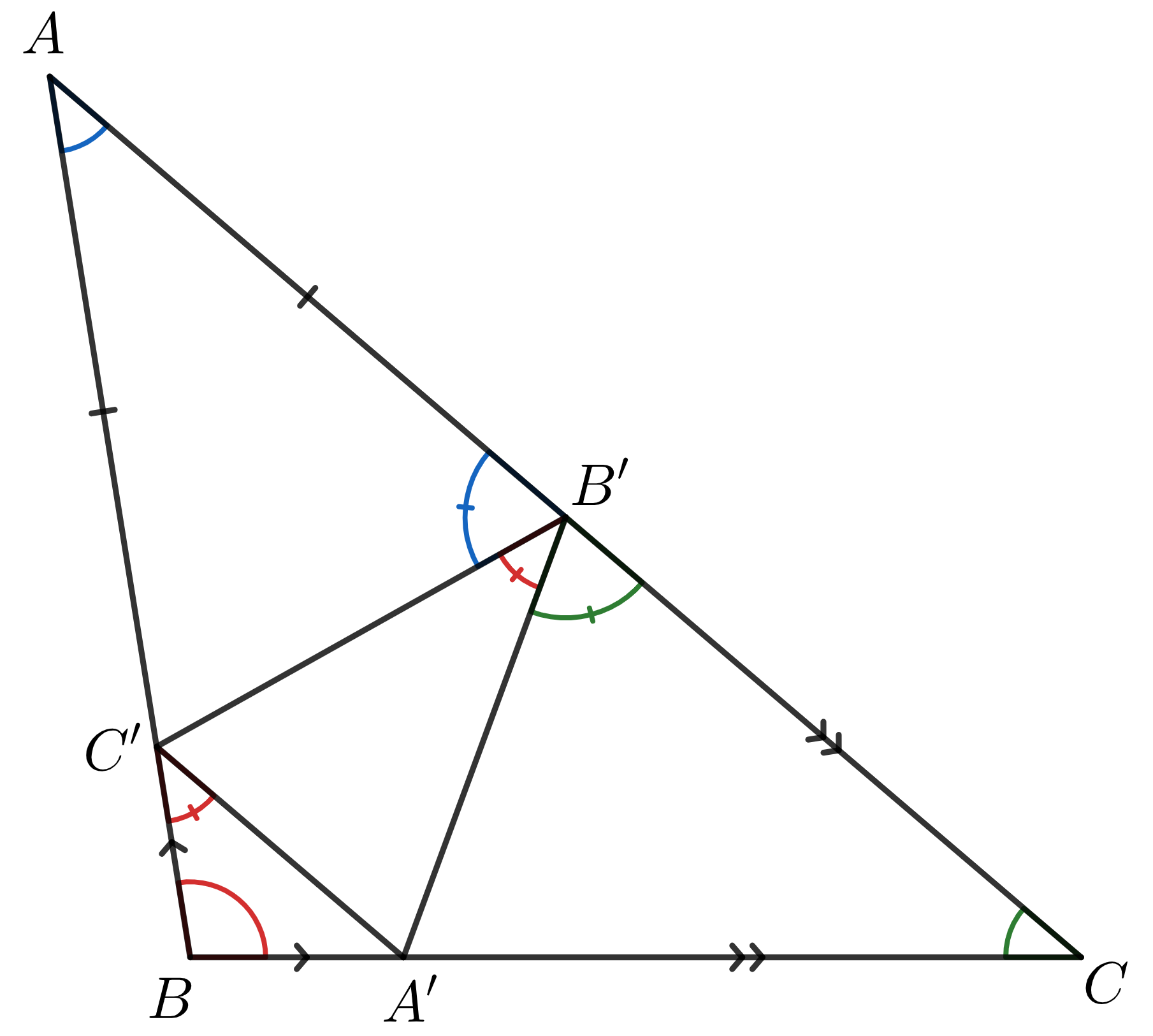
Uvažujme bežné označenie uhlov trojuholníka, čiže pri vrcholoch \(A, B, C\) sú postupne uhly \(\alpha, \beta, \gamma\). Zo súčtu uhlov v rovnoramennom trojuholníku \(AB'C'\) máme, že \(|\sphericalangle AB'C'|=90^\circ-\frac\alpha2\). Analogicky vieme dostať aj \(|\sphericalangle BC'A'|=90^\circ-\frac\beta2\) a \(|\sphericalangle CB'A'|=90^\circ-\frac\gamma2\). Nakoniec vieme vďaka \(\alpha+\beta+\gamma=180^\circ\) dopočítať veľkosť uhla \(\sphericalangle A'B'C'\) ako \[180^\circ-|\sphericalangle AB'C'|-|\sphericalangle CB'A'|=180^\circ-90^\circ+\frac\alpha2-90^\circ+\frac\gamma2=\frac{\alpha+\gamma}{2}=\frac{180^\circ-\beta}{2}=90^\circ-\frac\beta2.\] Z vety o obvodovom a úsekovom uhle preto vyplýva, že \(AB\) sa dotýka kružnici opísanej \(A'B'C'\). Toto vieme analogicky urobiť aj pre zvyšné strany, čím sa presvedčíme, že \(A', B', C'\) sú dotykové body kružnice vpísanej trojuholníku \(ABC\), keďže tá je jednoznačne určená.
Preto nám stačí zostrojiť na úsečkách \(HL, GL\) postupne body \(P, R\) také, že \(|HP|=|HS|\) a \(|GR|=|GS|\).
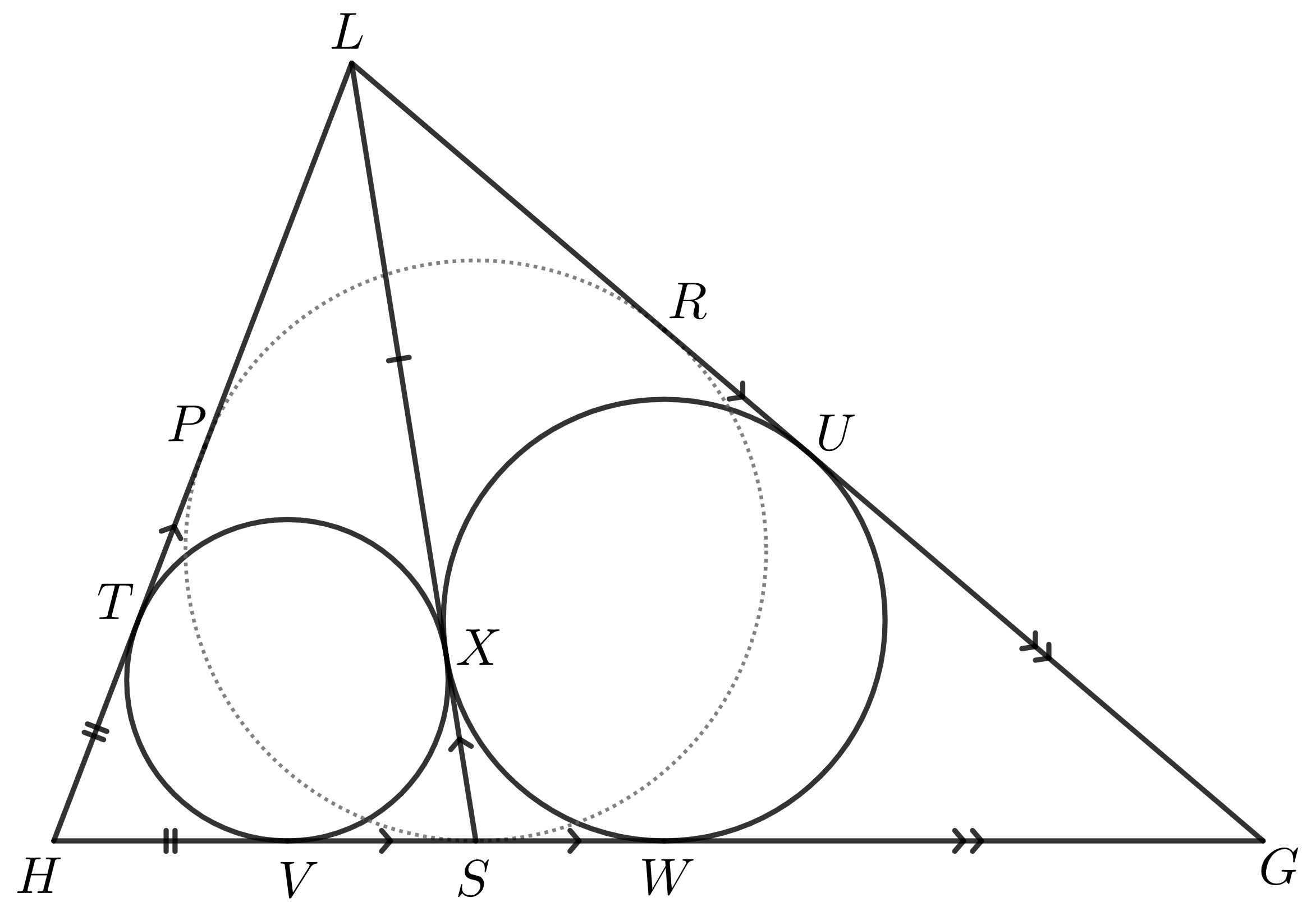
Ak pre ne platí aj \(|LP|=|LR|\), sme hotoví. A naozaj, \[\begin{align} |LP|&=|LT|+|HT|-|HP|=|LU|+|HV|-|HS|=|LU|-|VS|=\\ &=|LU|-|WS|=|LU|-|GS|+|GW|=|LU|+|GU|-|GR|=|LR|.\end{align}\] V skutočnosti však ešte treba overiť, že body \(P, R\) ležia vnútri úsečiek \(LH, LG\), a teda, že \(|HS|=|HP|<|HL|\). To však vyplýva z trojuholníkovej nerovnosti, ktorá hovorí, že \[\begin{align} |LH|+|LG|&>|HG|,\\ (|LT|+|TH|)+(|LU|+|UG|)&>|HV|+|VS|+|SW|+|WG|,\\ |LT|+|HV|+|LT|+|WG|&>|HV|+2|VS|+|WG|,\\ |LT|&>|VS|,\\ |LT|+|TH|&>|HV|+|VS|,\\ |HL|&>|HS|.\end{align}\]
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.