4. Kristínka Maľuje Štvorec vzorové riešenie

Chceme dokázať, že v každom takomto štvorci existuje dvojica bodov \(P,\,Q\) rovnakej farby, ktorých vzdialenosť je väčšia ako \(1,00778\, \mathrm{m}\). Môžeme to spraviť napríklad tak, že dokážeme, že štvorec, kde by všetky dvojice bodov rovnakej farby boli od seba vzdialené nanajvýš \(1,00778\, \mathrm{m}\) neexistuje (dôkaz sporom).

Prvá vec, ktorá hneď väčšinu z vás napadla bola, že keď máme tri farby a štyri vrcholy štvorca, aspoň dva vrcholy budú mať rovnakú farbu. Ak by malo existovať nejaké vyfarbenie štvorca, ktoré by odporovalo zadaniu, musia byť tieto dva vrcholy susedné. Keby totiž boli oproti sebe, teda spájala by ich uhlopriečka, boli by od seba vzdialené \(\sqrt{2}\), čo je viac ako \(1,00778\).

Tieto dva susedné vrcholy s rovnakou farbou si môžeme napríklad označiť \(A\) a \(B\), a povedzme, že ich farba je modrá. Keď chceme zistiť, kde všade ešte môžu byť modré body, nakreslíme si z bodov \(A\) aj \(B\) kružnice s polomerom \(1,00778\). Body mimo ich prieniku zjavne nemôžu byť modré, lebo by aspoň od jedného z bodov \(A\) alebo \(B\) boli ďalej ako \(1,00778\). Označme si prieniky týchto kružníc so stranami štvorca \(AD\) a \(BC\) postupne ako \(K\) a \(L\).

Teraz si vieme jednoducho vyrátať dĺžky úsečiek \(AK\) a \(BL\), keďže sú to odvesny pravouhlého trojuholníka s druhou odvesnou dĺžky \(1\) (strana \(AB\)) a preponou dĺžky \(1,00778\) (polomer naších kružníc). Z Pytagorovej vety bude \[|AK|=|BL|=\sqrt{{|BK|}^2 - {|AB|}^2}=\sqrt{1,00778^2 - 1^2} \approx 0,124982.\] Toto číslo nie je príliš pekné a zle by sa nám s ním počítalo ďalej. My ho však ani nepotrebujeme presné, môžeme si ho zaokrúhliť na \(0,125\), čo si vieme zapísať ešte krajšie ako \(\frac 1 8\). Dôležité je, že sme zaokrúhlili nahor, a teda bod ktorý bude ležať na \(AD\) a od bodu \(A\) bude vzdialený \(\frac 1 8\), bude ešte o kúsok ďalej aj od bodu \(B\).

Túto vzdialenosť budeme používať aj ďalej, na stranách \(AD\) a \(BC\) si vyznačíme body \(A_1,\, A_2,\, A_3,\, \dots,\, A_7\) a \(B_1,\, B_2,\, B_3,\, \dots,\, B_7\), tak, že sa nachádzajú v osminách oboch strán (teda \(AA_1 =\frac 1 8\), \(AA_2 = \frac 2 8,\, \dots,\, AA_7 = \frac 7 8\)). Len pre kontrolu, dĺžka úsečiek \(AB_1\) a \(BA_1\) bude \[|AB_1| = |BA_1| = \sqrt{1^2+{\frac 1 8}^2} = \frac 1 8 \sqrt{65} \approx 1,0077822185,\]

čiže o kúsok viac ako \(1,00778\).

Z toho jednoznačne vyplýva, že body \(A_1\) a \(B_1\) budú mať určite iné farby ako \(A,\,B\). Teraz máme dve možnosti.

1. Body \(A_1\) a \(B_1\) majú rovnakú farbu, povedzme, že červenú. Teraz sa môžeme pozrieť na body \(A_2\) a \(B_2\). \(A_2\) má znovu vzdialenosť od \(B_1\) rovnú \(\frac 1 8 \sqrt{65}\), čiže nemôže byť červený. Zároveň, vzdialenosť od \(B\) je ešte väčšia (je celkom zrejmé prečo), takže nemôže byť ani modrý. Bude teda zelený. Rovnakou úvahou, len symetricky otočenou, dôjdeme k tomu, že aj \(B_2\) musí byť zelený, lebo žiadna iná farba nám už nezostáva. Fajn, doteraz nám to sedelo, skúsme teda pokračovať. Bod \(A_3\) znova nemôže byť zelený kvôli bodu \(B_2\), červený kvôli \(B_1\) a modrý kvôli \(B\). Keďže máme k dispozícií len tri farby, \(A_3\) nemôže mať ani jednu z nich a každý bod musí byť ofarbený, prichádzame k sporu.

2. Body \(A_1\) a \(B_1\) majú rôzne farby, napríklad \(A_1\) je červený a \(B_1\) zelený. Teraz si pomôžeme bodom \(X\), ktorý umiestnime do stredu \(CD\). Vzdialenosť od oboch bodov k bodu \(X\) bude kvôli symetrií rovnaká a znovu ju vieme jednoducho vypočítať pomocou Pytagorovej vety: \[|A_1X| = |B_1X| = \sqrt{{|A_1D|}^2+{|DX|}^2} = \sqrt{{\frac 7 8}^2+{\frac 1 2}^2} = \frac 1 8 \sqrt{65}.\] Z toho nám vyplýva, že bod \(X\) nemôže byť ani červený ako \(A_1\), ani zelený ako \(B_1\) a nakoniec ani modrý ako \(A\) a \(B\). Týmto ho ale dostávame do rovnakej nepríjemnej pozície, v akej bol bod \(A_3\) v predchádzajúcom prípade, a nás dostávame k druhému sporu.

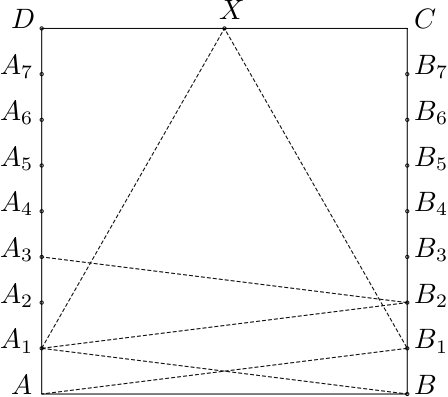
V oboch prípadoch sme narazili na spor, dokázali sme teda, že neexistuje také vyfarbenie štvorca, kde by žiadne dva body s rovnakou farbou neboli od seba ďalej ako \(1,00778\, \mathrm{m}\), čím sme vlastne dokázali tvrdenie zo zadania.