5. Koláč Mira Sýti (κ ≤ 7) vzorové riešenie

Zadanie. Betka upiekla pre Mr. Mira koláč, aby bol Mr. Miro spokojný. Koláč má tvar trojuholníka s dĺžkami strán \(19\), \(20\) a \(21\, \textrm{cm}\). Chce ho rozrezať pozdĺž jednej priamky na dva kusy a uložiť ich na kruhový tanier tak, aby sa neprekrývali ani nevyčnievali z taniera. Určte minimálny priemer taniera, pre ktorý sa to môže Betke podariť.

Máme pred sebou Mr. Mirov trojuholníkový koláč, ktorý sa chystáme rozrezať. Aby sme útvar, ktorý má najdlhšiu stranu \(a\) zmestili na tanier, zjavne potrebujeme tanier, ktorý má priemer aspoň \(a\), ináč by sa tam táto strana nevošla. Na úvod je podstatné uvedomiť si, že rez jednou úsečkou môže prejsť nanajvýš dvomi stranami trojuholníka (prechod cez vrchol nerátame). Jedna strana nám teda zostane neporušená. Táto strana bude dlhá aspoň \(19\ \text{cm}\), preto priemer Betkinho taniera bude mať najmenej \(19\ \text{cm}\).

Takto dostaneme štvoruholník s jednou stranou \(19\ \text{cm}\) a zostane nám ešte zvyšok koláča v podobe trojuholníka (viď obrázok).

Poďme skúsiť dokázať, že na tanier s priemerom \(19\ \text{cm}\) môžeme koláč uložiť. Budeme sa snažiť viesť rez čo najdlhšími stranami, „aby sme sa ich zbavili“ a koláč zmestili na čo najmenší tanier. O koláči budeme ďalej hovoriť ako o trojuholníku \(ABC\), v ktorom \(|AB| = 19\ \text{cm}\), \(|BC| = 20\ \text{cm}\), \(|CA| = 21\ \text{cm}\). Uložme teda trojuholník \(ABC\) na tanier tak, aby strana \(AB\) bola priemerom taniera. Body, v ktorých tanier (teda kružnica so stranou \(AB\) ako priemerom), pretína strany \(AC\) a \(BC\) (to sú tie s dĺžkami \(21\) a \(20\ \text{cm}\)) nazvime postupne \(P\), \(Q\). Náš koláč, trojuholník \(ABC\), rozrežeme pozdĺž priamky \(PQ\). Odrezali sme tak trojuholník \(PQC\), ktorý vyčnieval z taniera a ostal nám štvrouholník \(ABQP\), ktorý je celý uložený na tanieri. Potrebujeme už len ukázať, že sa k nemu na tanier zmestí aj trojuholník \(PQC\).

Keďže je štvoruholník \(ABPQ\) tetivový, budú uhly pri protiľahlých vrcholoch dávať súčet \(180\si{\degree}\). To, že \(|\sphericalangle BQP| = 180\si{\degree} - \alpha\) sa dá ukázať aj z toho, že oba sú obvobové uhly k tetive \(PB\), jeden s vrcholom na dlhšej časti oblúka \(PB\), druhý na jeho kratšej časti. Pre uhly \(\beta\) a \(180\si{\degree}-\beta\) analogicky. Preto \(|\sphericalangle QPC| = \beta\) a \(|\sphericalangle PQC| = \alpha\). Z toho dostávame, že trojuholníky \(ABC\) a \(QPC\) sú podobné.

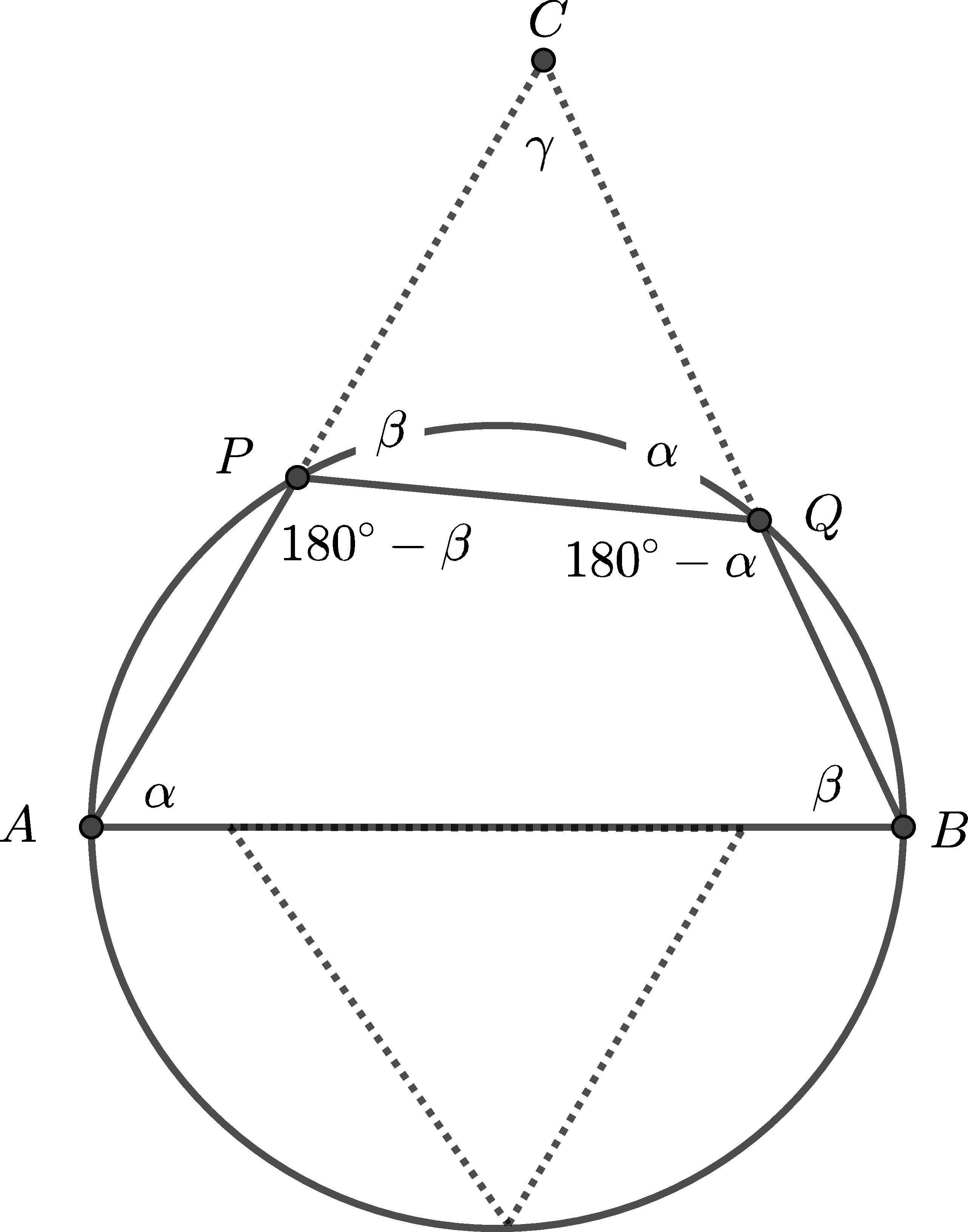
Máme teraz k dispozícii strany pôvodného trojuholníka, všetky uhly a podobnosť trojuholníkov. Ale ako na to? Ak si všimneme, polovica taniera je zatiaľ prázdna. Trojuholník \(PQC\) zmestíme na tanier, ak bude jeho najmenšia výška nanajvýš \(9,5\ \text{cm}\) (polomer taniera). Najmenšiu výšku má najdlhšia strana (to vieme zo vzťahu pre výpočet obsahu trojuholníka). To je tá, ktorá je oproti najmenšiemu uhlu. Tým je uhol \(\beta\), keďže je najmenší aj v trojuholníku \(ABC\). Potrebujeme teda zistiť výšku na stranu \(AP\) v pôvodnom trojuholníku a potom pomocou podobnosti zistiť hodnotu výšky na stranu \(QC\) v odkrojenom trojuholníku \(PQC\).

Na zistenie výšky použijeme trik. Porovnáme obsah, ktorý dostaneme pomocou Herónovho vzorca s obsahom, ktorý by sme dostali ako polovicu súčinu základne a výšky. Vieme, že obsah trojuholníka je \(S = b\cdot v_b/2\), resp. \(S^2 = b^2 \cdot v_b^2/4\). Ale podľa Herónovho vzorca platí aj \(S^2 =s(s-a)(s-b)(s-c)\), kde \(s\) je polovičný obvod, v našom prípade \(\frac{1}{2}(19+20+21) = 30\ (\text{cm})\). Odtiaľ dostávame \(S^2 = 29700\ \text{cm}^2\).

Teda \(S ^2 = 29700 = 441 v_b^2/4 = b ^2 v_b ^2/4\), z čoho vyplýva, že \[v_b = \sqrt{\frac{4\cdot29700}{441}} = \frac{20\sqrt{33}}{7} \doteq 16,41\ (\text{cm}).\]

Ďalším krokom bude zistenie koeficientu podobnosti trojuholníkov \(ABC\) a \(QPC\). Ten zistíme takto: Vezmeme si trojuholník \(APB\). V ňom poznáme \(|AB| = 19\), \(|\sphericalangle APB| = 90\si{\degree}\) (podľa Tálesovej kružnice) a dĺžku \(|PB| = v_b = 20\sqrt{33}/7\ \text{cm}\). To je dostatok na to, aby sme vyrátali \(|AP|\). Použitím Pytagorovej vety dostávame \[|AP| = \sqrt{19^2 - \left( \frac{20\sqrt{33}}{7}\right)^2} = \dfrac{67}{7}\ (\text{cm}).\] Potom \(|PC| = 21 - 67/7 = 80/7\ (\text{cm})\) . Keď dáme do pomeru strany oproti uhlu \(\alpha\), dostaneme koeficient podobnosti \[k = \dfrac{\frac{80}{7}}{20} = \dfrac{4}{7}.\]

Hurá, máme náš koeficient. Teraz prichádza prvá chvíľa napätia, či bude výška \(v_{CQ}\) na stranu \(CQ\) dlhá nanajvýš \(9,5\ \text{cm}\). Poďme na to. \(v_{CQ}:v_b = 4:7\), teda \[v_{CQ} = \frac{4}{7}v_b = \frac{4}{7}\cdot\frac{20\sqrt{33}}{7} = \frac{80\sqrt{33}}{49} \doteq 9,38 < 9,5\ (\text{cm}).\]

Výška by teda sedela. Aby sme však boli úplne spokojní, treba ukázať nielen to, že nebude prečnievať vrchol \(C\), ale že nebudú prečnievať ani ostatné vrcholy. Teda treba ukázať, že od päty kolmice na úcečku \(CQ\) (volajme ju \(Z\), na obrázku z dôvodu prehľadnosti nie je) po bod \(C\) aj \(Q\) je vzdialenosť nanajvýš \(9,5\ \text{cm}\). Z obrázka to síce vidno, ale obrázkový dôkaz nie je dôkaz. Teda chceme ukázať, že \(|ZQ| \leq 9,5\ \text{cm}\) aj \(|ZC| \leq 9,5\ \text{cm}\). Vec si ešte trocha zjednodušíme – ukážeme, že väčší z úsekov \(ZC\), \(ZQ\) bude stále menší ako \(9,5\ \text{cm}\). Pretože \(|PC| > |PQ|\), bude aj \(|ZC| > |ZQ|\) (dlhšej strane prislúcha väčšia časť úseku základne).

V pravouhlom trojuholníku \(ZCP\) platí: \[|ZC|^2 = |CP|^2-|ZP|^2= \left(\frac{4}{7}\cdot20\right)^2 - v_ {CQ}^2= \frac{102400}{2401}\ (\text{cm}),\] takže \(|ZC| = \sqrt{102400/2401}= 320/49\doteq 6,53 < 9,5\ (\text{cm})\). Keďže \(|ZQ| < |ZC|\), bude aj \(|ZC|<9,5\ \text{cm}\).

Teda rozrezaný koláč – štvoruholník aj trojuholníkový odrezok – sa zmestia na tanier s priemerom \(19\ \text{cm}\) a Betka nemusí behať do Ikey po väčší.