7. Kružnice Medziľudských Súvislostí (vzorové riešenie) - Korešpondenčný matematický seminár

Zadanie

Mr. Miro sa vo voľnom čase zaoberá medziľudskými pomermi. Pomery v geometrii sú však preňho easy, tie prenecháva vám.

Majme trojuholník $ABC$ s opísanou kružnicou $k$. Dotyčnice ku kružnici $k$ v bodoch $A$ a $B$ sa pretínajú v bode $T$. Kružnica opísaná trojuholníku $ABT$ pretína priamky $BC$ a $AC$ postupne v bodoch $D$ a $E$ ($D \ne B$ a $E \ne A$). Priamky $CT$ a $BE$ sa pretínajú v bode $F$. Predpokladajme, že bod $D$ je stredom úsečky $BC$. Určte pomer $|BF|:|BE|$.

Chceme zistiť pomer dĺžok dvoch úsečiek. Zatiaľ o nich nič nevieme, asi len toľko, že $|BE| > |BF|$, pretože bod $F$ je súčasť úsečky $BE$. V zadaní máme nejaké podmienky pre bod $D$, tak sa pozrime najprv naň, nakoľko sa všetko odvíja od jeho polohy. Označme $|\sphericalangle ACB|$ ako $\gamma$. K nemu sú $\sphericalangle BAT$ a $\sphericalangle ABT$ úsekové a teda ich veľkosť je tiež $\gamma$. Keďže súčet uhlov v trojuholníku je $180\si{\degree}$, vieme dopočítať $| \sphericalangle ATB|=180\si{\degree}-2\gamma$. Bod $D$ je tiež na kružnici opísanej trojuholníku $ATB$, tým pádom štvoruholník $ATBD$ je tetivový.

Súčet protiľahlých uhlov v tetivovom štvoruholníku je $180\si{\degree}$, preto $| \sphericalangle ADB|=2\gamma$. Uhol $CDA$ je k nemu susedný a má veľkosť $180\si{\degree} - 2\gamma$. Teraz sa pozrime na trojuholník $CDA$. Poznáme uhly pri vrcholoch $C$ a $D$. Dopočítaním veľkosti uhla pri vrchole $A$ dostaneme, že $|\sphericalangle CAD|=\gamma$. Tento trojuholník je rovnoramenný so základňou $AC$. Musí preto platiť, že $|AD|=|CD|$ a zo zadania vieme, že $|BD|=|CD|$, tieto tri dĺžky sú teda zhodné. Inak povedané vzdialenosť bodu $D$ od bodov $A$, $B$ a $C$ je rovnaká. Jediný bod, ktorý túto vlastnosť má, je stred kružnice opísanej trojuholníku $ABC$. Zjavne platí, že $BC$ je priemerom tejto kružnice. Z toho vyplýva, že kružnica opísaná trojuholníku $ABC$ je Tálesova kružnica a $|\sphericalangle CAB|=90\si{\degree}$.

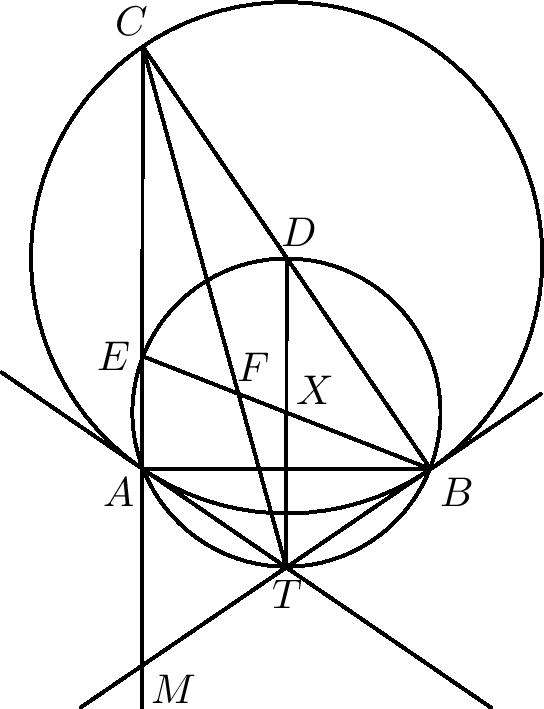
Označme prienik priamok $AC$ a $BT$ ako $M$. O uhle $CBM$ vieme, že má veľkosť $90\si{\degree}$ (pretože je to aj uhol $DBT$ a $BT$ je dotyčnica kolmá na $DB$). Štvoruholník $DBTE$ je tetivový, a tak aj $|\sphericalangle DET|=90\si{\degree}$. Úsečky $DE$ a $BT$ sú kolmé na $BD$ a sú rovnobežkami. Nakoľko je bod $D$ stred strany $BC$ a úsečka $DE$ je rovnobežná s $BT$, respektíve s $BM$, tak úsečka $DE$ je stredná priečka v trojuholníku $MBC$ a bod $E$ je stred strany $MC$.

Označme stred kružnice opísanej trojuholníku $ATB$ ako $X$. Vieme, že $|XE|=|XT|=|XD|=|XB|$. Uhly $BXD$ a $EXT$ sú vrcholové, čo znamená, že sú zhodné. Preto aj trojuholníky $BXD$ a $EXT$ sú zhodné. Z toho vyplýva, že úsečky $ET$ a $BD$ sú rovnobežné a aj $ET$ je stredná priečka. V trojuholníku $MCB$ sú úsečky $BE$ a $CT$ ťažnice. Pretínajú sa v bode $F$. Ťažnice sa navzájom delia v pomere $1:2$, pričom dĺhší úsek je ten pri vrchole. Hľadaný pomer je preto $|BF|:|BE|=2:3$.

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.

7. Kružnice Medziľudských Súvislostí vzorové riešenie

Zadanie

Diskusia