Zadanie
Kapitán sa zapozeral do lodného radaru, aby si pozrel, kde pristáť. Radar ohraničuje kružnica \(r\), na ktorej ležia body \(A\), \(B\), \(C\), \(D\) tak, že úsečky \(AC\) a \(BD\) sú na seba kolmé. Kapitán si zobral priamku \(AC\) a jej obraz v osovej súmernosti podľa osi uhla \(BAD\) označil \(g\). Dokážte, že priamka \(g\) prechádza stredom kružnice \(r\).
Keďže sa jedná o geometrickú úlohu, skúsme začať tým, že si nakreslíme obrázok. Ten náš by mohol vyzerať napríklad nejak takto:
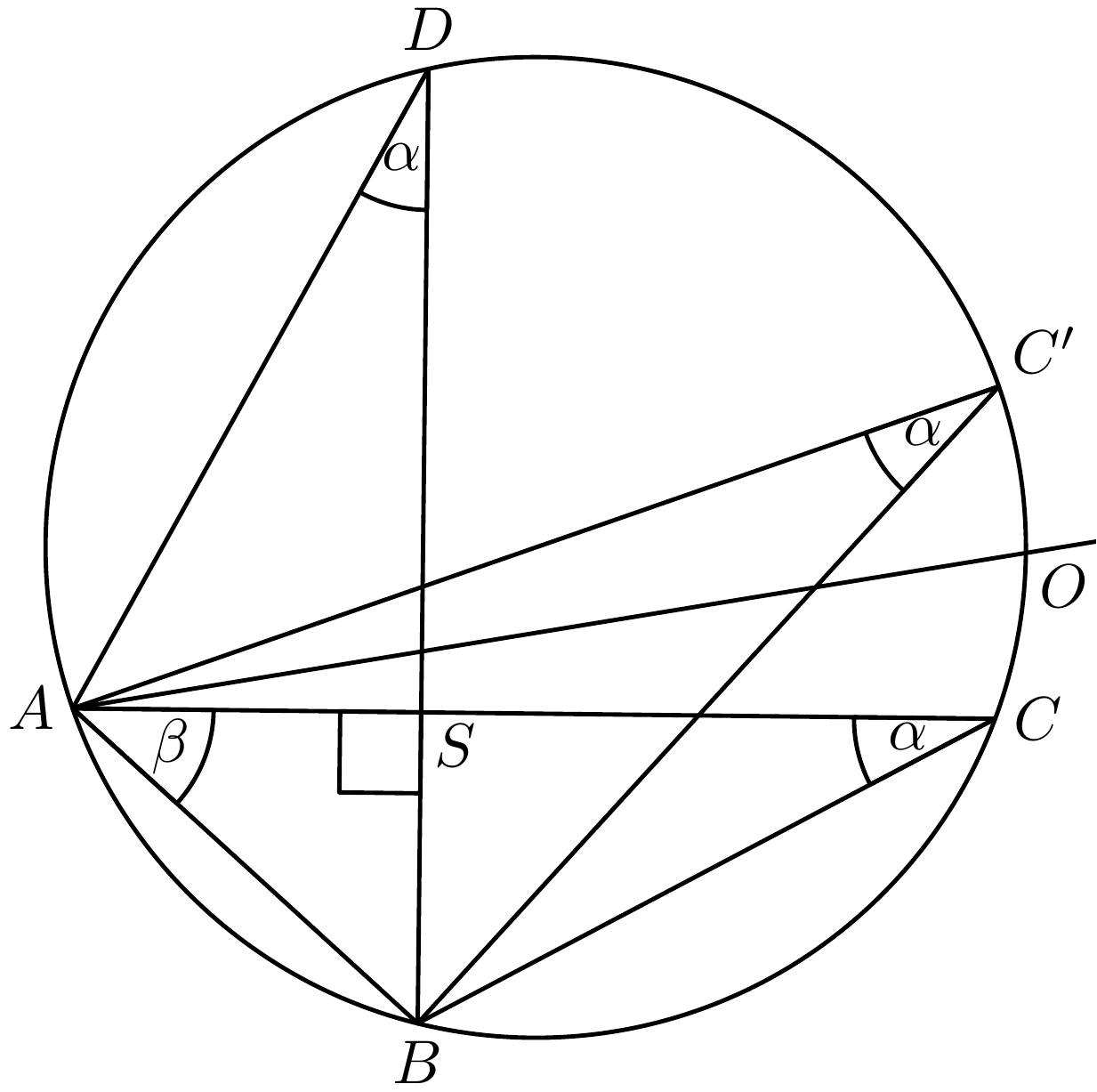
Vidíme, že niektoré uhly sme si už doplnili. V prvom rade nás budú zaujímať uhly \(\alpha\), ktoré sme doplnili pri bodoch \(C\), \(C'\) a \(D\). O tom, že tieto uhly majú rovnakú veľkosť sa presvedčíme veľmi jednoducho a síce tak, že všetky sú obvodovými uhlami k úsečke \(AB\). Pomocou nich si vieme ľahko dopočítať z pravouhlých trojuholníkov, že \(|\sphericalangle SAD|=90^\circ - \alpha = |\sphericalangle CBS|\). Na obrázku ešte vidíme, že uhol \(\sphericalangle BAC\) sme si označili \(\beta\), pretože ho budeme často používať a zjednoduší nám to prácu.
Ďalej vidíme, že vcelku zaujímavú rolu bude zohrávať os uhla \(BAD\). Skúsme si tento uhol preto vyjadriť. Hneď vidíme, aká bude veľkosť tohoto uhla a síce \(|\sphericalangle BAD|=90^\circ - \alpha + \beta\). Keďže ho os delí na polovicu, bude platiť: \[|\sphericalangle BAO|=\frac {90^\circ - \alpha + \beta}{2}.\]
Uvedomíme si, že \(|\sphericalangle CAO|=|\sphericalangle C'AO|\) (zo zadania z osovej symetrie). Tento uhol vieme teraz jednoducho zistiť ako: \(|\sphericalangle CAO|=|\sphericalangle BAO|-|\sphericalangle BAC|\), teda: \[|\sphericalangle CAO|=\frac {90^\circ - \alpha + \beta}{2} - \beta = \frac {90^\circ - \alpha - \beta}{2}.\] Môžete sa skúsiť zamyslieť, ako by to vyzeralo v prípade, že by sa bod \(C\) nachádzal nad osou súmernosti \(AO\) (tento podobný prípad ako aj jeho pokračovanie nechávame na čitateľa). Vďaka tomuto všetkému si už vieme ľahko dopočítať aj veľkosť uhla \(BAC'\) ako: \[ \begin{aligned} |\sphericalangle BAC'|&=|\sphericalangle BAC|+|\sphericalangle CAO|+|\sphericalangle OAC'|,\\ |\sphericalangle BAC'|&=\beta + 2\cdot \frac {90^\circ - \alpha - \beta} {2}=90^\circ - \alpha. \end{aligned} \] Teraz už vieme veľkosti dvoch uhlov v \(\triangle BAC'\) a ľahko si dopočítame, že veľkosť posledného uhla je: \[|\sphericalangle ABC'|=90^\circ.\] V tomto momente je nám už všetko jasné. Keďže nám vyšiel uhol \(ABC'\) pravý, znamená to, že kružnica \(r\) je v skutočnosti Tálesovou kružnicou nad úsečkou \(AC'\) a teda úsečka \(AC'\) musí prechádzať stredom kružnice \(r\), čo sme presne chceli dokázať.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.