Zadanie
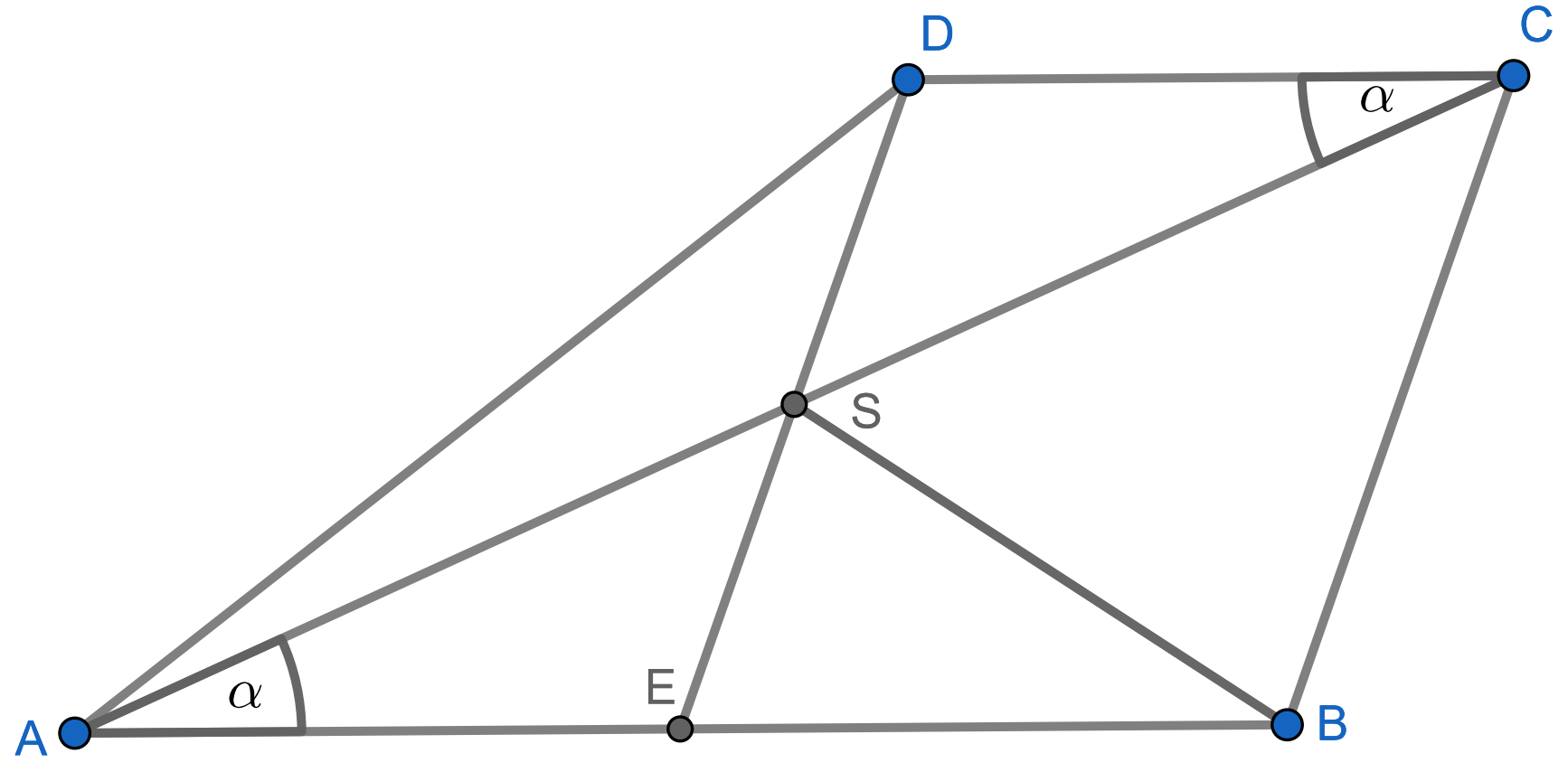
Na svojom tanieri našiel Jožo nakreslený štvoruholník \(ABCD\), ktorý mal strany \(AB\) a \(CD\) rovnobežné. Na uhlopriečke \(AC\) bol v strede vyznačený bod \(S\). Jožo si všimol, že trojuholníky \(ABS\) a \(ACD\) majú rovnaký obsah a hneď vyhlásil, že priamka \(DS\) je preto rovnobežná s priamkou \(BC\). Mal Jožo pravdu? Ak áno, ako na to prišiel? Ak nie, prečo?
Potrebujeme nejakým spôsobom využiť znalosť že trojuholníky ABS a ACD majú rovnaký obsah. Obsah trojuholníka \(XYZ\) vieme vypočítať podľa vzorca \(S = \frac{1}{2}|XY||XZ| \sin{|\sphericalangle YXZ|}\). Všimnime si že uhly \(CAB\) a \(ACD\) sú striedavé a teda \(|\angle SAB| = |\angle ACD|=\alpha\).
Podľa zadania \[\begin{aligned} \frac{1}{2}|AB||AS| \sin{\alpha} = S_{\triangle ABS} = S_{\triangle ACD} = \frac{1}{2}|CA||CD| \sin{\alpha}.\end{aligned}\] Sínusy v \((1)\) sú rovnaké, preto sa vykrátia. 1
Zo zadania vieme \(2|AS| = |CA|\). Po dosadení poslednej rovnosti do \((1)\) dostaneme \[|AB| = 2|CD|.\]
Označme priesečník priamky \(AB\) a \(DS\) ako bod \(E\).
Z toho že uhly \(ASE\) a \(CSD\) sú vrcholové a teda rovnako veľké, vyplýva, že trojuholníky \(ASE\) a \(CSD\) majú rovnaké 2 uhly (teda všetky 3) a pretože \(|AS| = |CS|\), sú zhodné. Potom \(|AE| = |CD| = \frac{1}{2}|AB|\), takže \(|BE| = |AB|-|AE| = |CD|\). Ďalej vieme, že uhly \(CDB\) a \(EBD\) sú navzájom striedavé, a teda rovnako veľké. Trojuholníky \(EBD\) a \(CBD\) sú zhodné podľa vety \(sus\), pretože majú rovnaké veľkosti strán \(EB\) a \(CD\), majú spoločnú stranu, a platí \(|\sphericalangle EBD| = |\sphericalangle BDC|\).
Z toho vyplýva \(|DE| = |BC|\). Teda \(EBCD\) je rovnobežník, a priamka \(DE\) je totožná s priamkou \(DS\), teda \(DS\) a \(BC\) sú rovnobežné.
Zrejme sínus toho uhla nemôže byť \(0\), lebo ten uhol by musel mať hodnotu \(0^{\circ}\) alebo \(180{\circ}\) a to v trojuholníku nie je možné↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.