1. Kružnicové Máriine Šaty vzorové riešenie

Polomer \(r\) kružnice vpísanej trojuholníku \(KEL\) vieme vyjadriť pomocou obsahov trojuholníkov. Označme si stred tejto kružnice ako \(S\). Z náčrtu vidíme vzťah pre obsah trojuholníka \(EKL\) a obsahy trojuholníkov \(EKS\), \(KLS\) a \(LES\): \[\tag{1} S_{EKL}=S_{EKS}+S_{KLS}+S_{LES}.\]

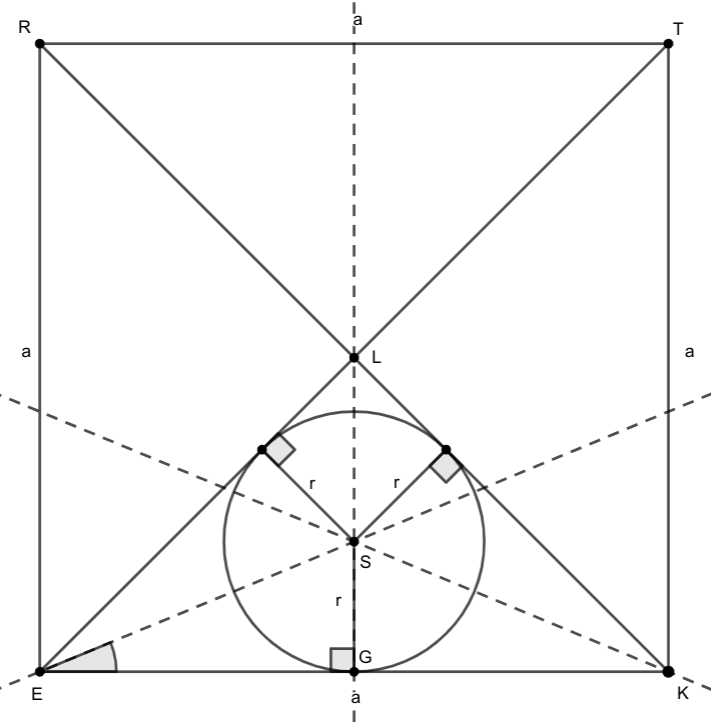
Vieme, že uhlopriečky štvorca rozdeľujú štvorec na štyri zhodné trojuholníky. Tým pádom vieme určiť obsah trojuholníka \(EKL\) ako štvrtinu obsahu štvorca \(REKT\): \[S_{EKL}=\frac{1}{4}S_{REKT}=\frac{1}{4}a^2.\] Obsah trojuholníka \(EKS\) vieme vyjadriť ľahko, nakoľko poznáme dĺžku jeho strany a aj dĺžku výšky na túto stranu: \[S_{EKS}=\frac{1}{2}r|EK|=\frac{ar}{2}.\] Pri trojuholníkoch \(KLS\) a \(LES\) musíme spraviť o krok navyše, nakoľko nepoznáme dĺžku ich strany. Tú však vieme zistiť pomocou Pytagorovej vety z trojuholníka \(EKT\) alebo \(EKL\) alebo môžeme využiť relatívne známy poznatok, že pomer uhlopriečky štvorca a jeho strany je \(\sqrt{2}\), čiže \(|EL|=\frac{\sqrt{2}}{2}a\), pomocou čoho vieme ľahko vyjadriť obsahy \[S_{KLS}=S_{LES}=\frac{1}{2}\frac{a\sqrt{2}}{2}r=\frac{ar\sqrt{2}}{4}.\] Doplnením všetkých týchto obsahov do (1) dostávame vzťah pre stranu štvorca \(a\) a polomer vpísanej kružnice \(r\): \[\begin{align} \frac{1}{4}a^2&=\frac{ar}{2}+\frac{ar\sqrt{2}}{4}+\frac{ar\sqrt{2}}{4},\\ \frac{1}{4}a^2&=\frac{ar}{2}+\frac{ar\sqrt{2}}{2},\\ \frac{1}{2}a^2&=ar\left(1+\sqrt{2}\right),\\ \frac{1}{2\left(1+\sqrt{2}\right)}a&=r,\\ r&=\frac{\sqrt2-1}{2\left(\sqrt2+1\right)\left(\sqrt2-1\right)}a=\frac{\sqrt2-1}{2\left(2-1\right)}a=\frac{\sqrt{2}-1}{2}a.\end{align}\] V poslednom kroku sme urobili tzv. usmernenie zlomku. Pomocou vzorca \((A-B)(A+B)=A^2-B^2\) sme sa zbavili odmocniny v menovateli.

Iné riešenie.

Alternatívne sme mohli na získanie tohto vzťahu využiť trigonometriu v trojuholníku \(EGS\), kde \(G\) je stred strany \(EK\). Vieme vyjadriť tangens uhla \(GES\) ako \[\tan(|\sphericalangle GES|)=\frac{|GS|}{|EG|}=\frac{r}{\frac{1}{2}a}.\] Z tohoto vzťahu vieme vyjadriť polomer kružnice: \[r=\frac{1}{2}a\tan(|\sphericalangle EGS|).\] Veľkosť uhla \(GES\) vieme ľahko zistiť na základe toho, že stred \(S\) vpísanej kružnice leží na priesečníku osí uhlov trojuholníka \(EKL\). Uhol \(KEL\) má \(45^\circ\), tým pádom musí mať uhol \(GES\) \(22,5^\circ\). Hodnota \(\tan(22,5^\circ)\) nie je úplne bežne známa, no dá sa zistiť napríklad použitím vzorca pre polovičný uhol tangensu, ktorý je \[\tan\frac x2 = \frac{1-\cos x}{\sin x}.\] Z toho však vieme prísť na to, že \(\tan(22,5^\circ)=\sqrt{2}-1\), vďaka čomu dostaneme vzťah pre polomer kružnice \[r=\frac{1}{2}a(\sqrt{2}-1).\]