10. Kapitola Medzipriestorového Štvoruholníka vzorové riešenie

Predtým, než začneme úlohu riešiť, zamyslime sa najprv nad dvomi predprípravnými vecami – po prvé, ako vôbec takýto komplikovaný obrázok s dvomi predpokladmi nakresliť a po druhé (čo súvisí s kreslením), aké má táto konfigurácia stupne voľnosti. Voľne povedané, počet stupňov voľnosti je v podstate počet objektov, ktoré môžeme postupne zakresliť do roviny tak, že pri kreslení každého z nich máme stále nejakú voľnosť vo výbere jeho polohy a zároveň stále dodržiavame predpoklady zo zadania. Napríklad, rovnostranný trojuholník žiadne stupne voľnosti nemá, ak si odmyslíme štandardné zhodné a podobné zobrazenia v rovine. Ak fixneme veľkosť, polohu a rotáciu trojuholníka, nemáme už nič, čím by sme mohli voľne hýbať, pretože vzájomná poloha jeho vrcholov je fixne daná.

Správnych spôsobov, ako úlohu nakresliť, môže byť niekoľko. My odprezentujeme ten, ktorý sa zdá nám najvhodnejší. Silno odporúčame čitateľovi zobrať papier a pero a kresliť s nami, aby videl, aké je to v tomto poradí jednoduché. Najmä, ak mal problémy so svojím vlastným náčrtom. Začneme kružnicou \(k\). Toto rozhodnutie je jasné každému, kto sa kedy snažil nakresliť dotyčnicový štvoruholník tak, že najprv nakreslil jeho strany. Fixneme si jej polohu a veľkosť, aby sme sa zbavili zbytočnej voľnosti v podobe posunutí a rovnoľahlosti. Môže to znieť neintuitívne, ale ako druhý objekt nakreslíme priamku, na ktorej budú ležať vrcholy \(C, D\). Onedlho uvidíme, prečo. Túto priamku nakreslíme tak, aby bola „vodorovne“ a hore. Priesečník tejto priamky s kružnicou \(k\) označme \(H\). Teraz zvoľme vrchol \(D\) kdekoľvek na tejto priamke naľavo od \(H\).

Tak a sme hotoví. Akokoľvek neuveriteľne to bude znieť, práve sme vyčerpali všetky stupne voľnosti, ktoré sme mali. Celý zvyšok konfigurácie je daný tým, čo sme zrovna nakreslili. Zároveň je ľahké si rozmyslieť, že kresliac veci v tomto poradí sme nestratili žiadnu „skrytú konfiguráciu“ a vieme takto nakresliť všetky. Prečo je teda celý zvyšok obrázku daný?

Poloha bodu \(F\) (a teda aj priamky, na ktorej ležia body \(D, A\)) je daná dokreslením druhej dotyčnice z \(D\) na \(k\). Nazvime si kružnicu opísanú trojuholníku \(DFX\) ako \(l\). Všimnime si, že poloha tejto kružnice je teraz jasne daná aj bez bodu \(X\), lebo zo zadania vieme, že sa dotýka priamky \(DC\). Teda stačí pretnúť kolmicu na priamku \(DC\) prechádzajúcu bodom \(D\) s osou úsečky \(FD\) a máme jednoznačne určený stred, označme ho \(T\). Toto je zároveň dobrý spôsob, ako kružnicu nakresliť. Teraz môžeme jednoducho označiť druhý priesečník kružníc \(k, l\) ako \(X\). Ďalej vieme skonštruovať priamku \(DX\). Jej druhý priesečník s kružnicou \(k\) musí byť bod \(E\). V tomto bode teraz máme určenú dotyčnicu ku kružnici \(k\), ktorá je priamkou, na ktorej musia ležať body \(B, C\). Bod \(C\) je už jednoznačne určený ako priesečník tejto priamky a priamky \(DH\), teda ho označíme. Aby sa kružnica \(l\) mohla dotýkať priamky \(AB\), musí byť táto priamka druhou spoločnou dotyčnicou kružníc \(k, l\), lebo vieme, že \(AB\) sa zo zadania dotýka aj kružnice \(k\). Teda poloha priamky \(AB\) je jednoznačne určená a tým aj body \(A, B\) ako priesečníky tejto dotyčnice postupne s priamkami \(DF\) a \(CE\). Ako vidíme, vskutku sme práve nakreslili celý obrázok pričom každý jeden krok bol veľmi jednoduchý na reálne nakreslenie. Popri kreslení sme už stihli získať slušnú intuíciu o konfigurácií a jej vnútorných väzbách.

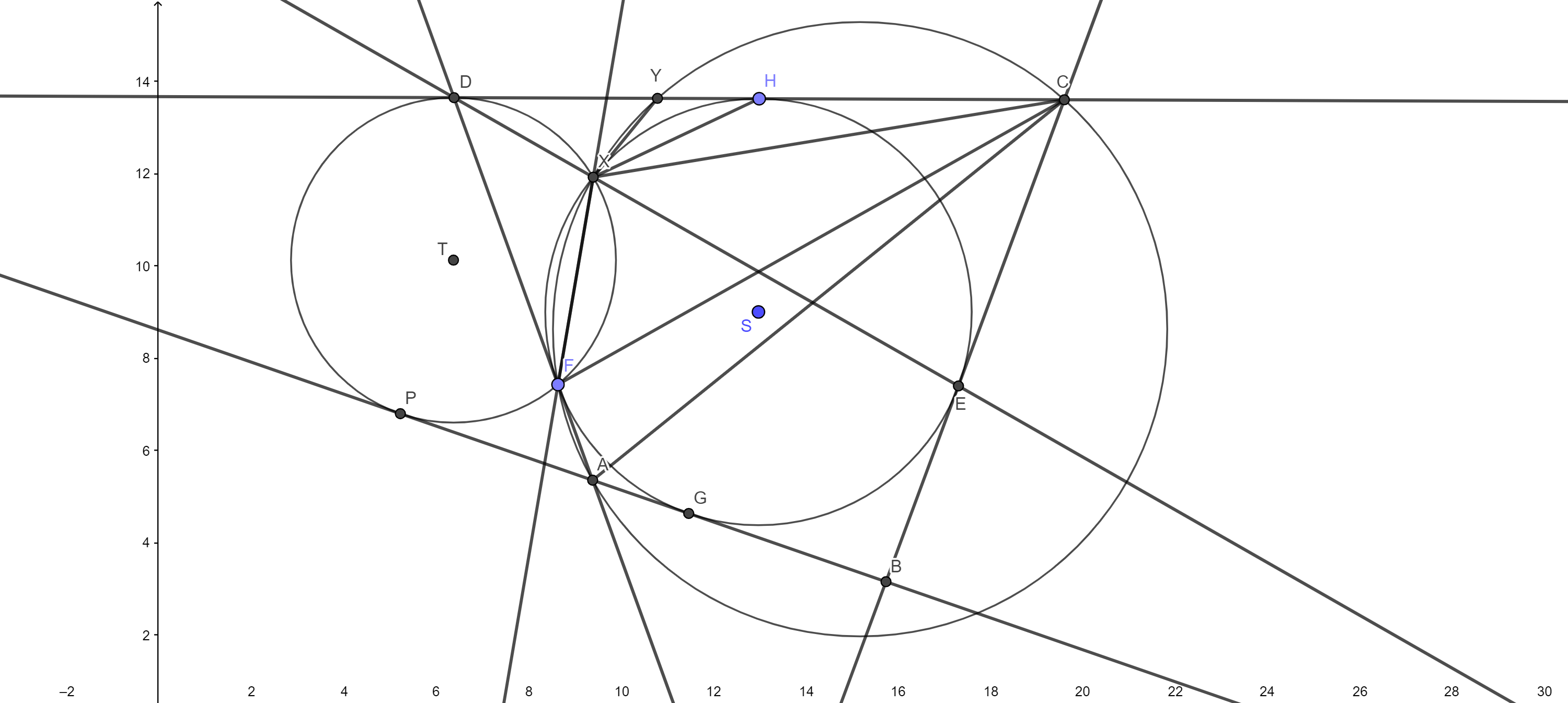
Tak a teraz prejdime na samotné riešenie. Stačí už len ukázať, že kružnica opísaná trojuholníku \(XFC\) (nazvime ju \(m\)) prechádza bodom \(A\). Na to označíme bod \(A'\) ako priesečník kružnice \(m\) s priamkou \(AB\) a ukážeme, že \(A'\) a \(A\) sú vlastne na tom istom mieste.¹ Plán je nasledovný: stačí nám vlastne dokázať, že priamka \(A'F\) je dotyčnicou ku kružnici \(k\). Potom to musí byť tá istá dotyčnica, ktorá z bodu \(D\) vedie cez \(F\) do bodu \(A\). Ako ukážeme, že \(A'F\) je dotyčnicou? Začneme tým, že sa namiesto tejto časti obrázka budeme sústrediť na symetrickú časť obrázka s bodmi \(X\), \(H\) a a priesečníkom kružnice \(m\) s priamkou \(DC\) (ktorý nazveme \(Y\)). To preto, lebo v tej časti obrázka máme trochu viac informácií a trochu jednoduchšie uhlenie. Ukážeme, že priamka \(YX\) je dotyčnicou kružnice \(k\).

Poďme sa pustiť do uhlenia. Označme stred kružnice \(k\) ako \(S\), priesečník kružnice \(m\) s priamkou \(DC\) ako \(Y\) a priesečník \(AB\) s kružnicou \(k\) ako \(G\). Nech \(|\angle FDH| = 2\alpha\) a \(|\angle XDH| = \omega\). Hoci \(\omega\) je daná priamo z \(\alpha\), ich vzájomný vzťah nie je priamočiary a jednoduchý, preto sa oplatí označiť aj \(\omega\), ktorý budeme masívne používať. Keďže \(DH\) je dotyčnicou ku kružnici \(l\), z vety o úsekovom uhle nám je jasné, že \(|\angle DFX| = \omega\). Keďže priamka \(DF\) je dotyčnicou ku kružnici \(k\), z vety o úsekovom uhle nám je jasné, že \(|\angle FEX| = \omega\). To ale znamená, že priamky \(DC\) a \(EF\) sú rovnobežné (vďaka striedavým uhlom)! Ľahko sa dá rozmyslieť, že v takejto situácií to musí znamenať, že štvoruholník \(DCEF\) je nie len lichobežník, ale aj rovnoramenný lichobežník (napríklad tak, že si predstavíme konfiguráciu, v ktorej naozaj tento štvoruholník bude rovnoramenný lichobežník (a teda \(H\) bude stredom úsečky \(DC\)) a uvedomíme si, že posunom bodu \(C\) v ktoromkoľvek smere sa monotónne bude meniť aj poloha bodu \(E\), čo pri fixnej polohe bodu \(F\) zamedzuje rovnobežnosti daných dvoch priamok). Teda \(|\angle CFD| = |\angle CED| = 180-\omega-2\alpha\) (čo vidíme dopočítaním uhlov do \(180\) stupňov v trojuholníku \(DEC\)). Teda uhol \(XFC\) musí mať veľkosť \(180-2\omega-2\alpha\), po odpočítaní uhla \(DFX\). Keďže body \(FXYC\) ležia na kružnici, využitím, že súčet protiľahlých uhlov tetivového štvoruholníka je 180 stupňov, vidíme, že \(|\angle XYH| = 2\omega+2\alpha\).

Ďalej, \(|\angle HSF|=180-2\alpha\) ako jasne vidno z tetivového štvoruholníka \(DFSH\). Zároveň, \(|\angle XSF|=2\omega\) keďže uhol \(XSF\) je stredový k uhlu \(XEF\). Teda jednoduchým odpočítaním uhlov dostávame \(|\angle HSX|=180-2\alpha-2\omega\). Ak teraz označíme \(Y'\) ako priesečník dotyčnice ku kružnici \(k\) prechádzajúcej bodom \(X\) a priamky \(DC\) a dopočítame z tetivovosti štvoruholníka \(XSHY'\) uhol pri \(Y'\), vidíme, že je to ten istý uhol ako uhol pri \(Y\) v trojuholníku \(XYH\). Teda \(Y\) a \(Y'\) splývajú. Z toho vyplýva, že druhá dotyčnica z bodu \(Y\) na kružnicu \(k\) je vlastne \(YX\).

Záverom, všimnime si, že všetky tri kružnice a tiež body \(X, F, H, G, A', Y\) sú súmerné vzhľadom na osovú súmernosť s osou \(TS\), teda osou tvorenou stredmi kružníc \(k, l\) (a \(m\)). Teda páry bodov \(X, F\) a \(Y, A'\) a \(H, G\) majú symetrické pozície a role vzhľadom na os \(ST\). To ale znamená, že druhá dotyčnica na kružnicu \(k\) z bodu \(A'\) nie je nič iné, ako \(A'F\), symetricky k vzťahu bodov \(Y\) a \(X\). Nakoľko dotyčnica v bode \(F\) ku kružnici \(k\) je len jedna, musí to byť tá istá dotyčnica, na ktorej ležia body \(F, A\). Teda vskutku, \(A\) a \(A'\) ležia na tom istom mieste, čo bolo našim cieľom dokázať.

Poznámka na rozlúčku: Bod \(Y\) v tomto riešení nebol nevyhnutný. Celá vec sa dala spraviť počítaním uhlov pri \(A\) a \(A'\), s využitím iba o trošičku náročnejšieho uhlenia. Teda táto úloha sa dala vyriešiť vskutku minimalisticky, s využitím najzákladnejších geometrických tvrdení a bez dokresľovania bodov a priamok. Bod \(Y\) sme dokreslili, iba aby sme demonštrovali, že nie je potrebné sa báť robiť také veci, ak máme dôvod veriť, že nám to pomôže.