3. Krabice Máme Skryté $\left(\kappa \le 3\right)$ vzorové riešenie

Zadanie

Krab chcel zbaliť krabicu, no už nemal žiadnu voľnú…

Štvorce \(BCDE\) a \(FGHI\) sú v trojuholníku \(ABJ\) tak ako na obrázku 1, pričom bod \(E\) je stred strany \(AB\), \(C\) je stred strany \(FG\), body \(D\) a \(I\) ležia na strane \(AJ\), bod \(G\) leží na strane \(BJ\) a bod \(F\) leží na strane \(CD\). Akú časť trojuholníka \(ABJ\) tvorí štvorec \(BCDE\)?

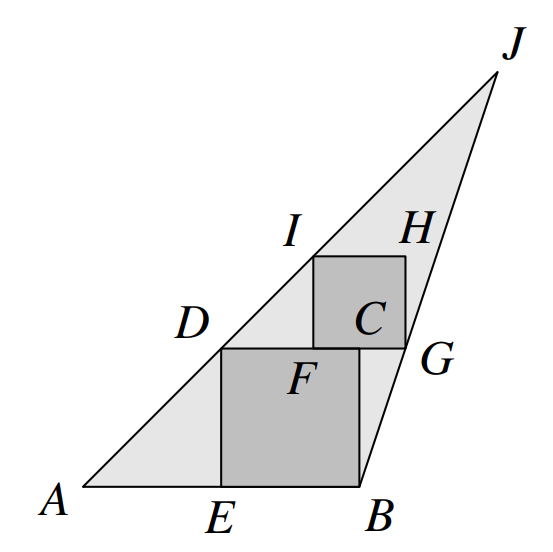
Keďže bod \(E\) je stredom strany \(AB\) a \(BCDE\) je štvorec, musí byť trojuholník \(DAE\) rovnoramenný. Nakoľko je uhol pri bode \(E\) pravý, musia mať ostatné uhly v trojuholníku \(DAE\) \(45^\circ\). Vďaka rovnobežnosti \(EB\) a \(DC\) taktiež vieme povedať, že aj trojuholník \(IDF\) musí mať uhly pri základni veľkosti \(45^\circ\), a teda je taktiež rovnoramenný.

Teraz by nás mohlo zaujímať, aká dlhá je strana štvorca \(FGHI\) v porovnaní s \(BCDE\). Keďže bod \(C\) je stredom strany \(FG\), úsečka \(FC\) je polovicou zo strany štvorca \(FGHI\). Avšak z rovnostrannosti \(IDF\) vyplýva, že \(|DF| = |FI|\), a teda \(|DC| = |IF| + |CF|\), čiže strana veľkého štvorca je rovnako dlhá ako \(\frac32\) strany malého štvorca (alebo naopak, strana malého štvorca je \(\frac23\) z veľkého).

Všimnime si, že trojuholníky \(ABJ\) a \(DGJ\) sú si podobné, nakoľko majú rovnaké uhly. Vieme, že strana \(AB\) je dvakrát tak dlhá ako úsečka \(EB\) a zistili sme, že strana \(DG\) je \(\frac43\) z dĺžky \(EB\). Tým pádom vieme aj určiť koeficient podobnosti týchto dvoch trojuholníkov, a to je \(\frac{4/3}{2} = \frac23\). Na tento koeficient sme mohli prísť aj uvedomením, že musí byť rovnaký s koeficientom podobnosti štvorcov \(BCDE\) a \(FGHI\), nakoľko bod \(F\) je takisto stredom strany \(DG\), rovnako ako bod \(E\) na strane \(AB\), a body \(I\) a \(G\) sa taktiež dotýkajú strán trojuholníka.

Pri koeficientoch podobnosti platí, že obsah podobných útvarov sa zväčšuje/zmenšuje s druhou mocninou koeficientu. Pre trojuholník si to vieme dokázať pomocou vzorca pre výpočet obsahu \(S=a\cdot v_a\). Ak máme dva trojuholníky s koeficientom podobnosti \(k\), potom musí byť strana a výška druhého trojuholníka rovná \(ka\), resp. \(kv_a\), a jeho obsah je \(ka\cdot kv_a = k^2av_a\), čo je práve \(k^2\) krát obsah prvého trojuholníka. Tento vzťah platí aj vo všeobecnosti pre všetky útvary, a analogicky sa taktiež pri priestorových telesách objem škáluje s treťou mocninou koeficientu podobnosti. My vieme tento fakt využiť na výpočet obsahu \(DGJ\), ktorý tým pádom tvorí \(\left(\frac23\right)^2 = \frac49\) z obsahu \(ABJ\).

Nakoniec si musíme dopočítať obsah trojuholníkov \(DAE\) a \(BGC\). Vďaka rovnostrannosti \(DAE\) vieme, že musí mať polovicu z obsahu \(BCDE\), a keďže \(CG\) je \(\frac13\) z \(EB\), musí mať \(BGC\) obsah \(\frac16\) z \(BCDE\).

Zostáva nám už len všetky tieto obsahy sčítať a vyjadriť si z nich obsah \(BCDE\) relatívne k \(ABJ\).

\[\begin{align} S_{\triangle ABJ} &= S_{\triangle AED} + S_{\square BCDE} + S_{\triangle BGC} + S_{\triangle DGJ},\\ S_{\triangle ABJ} &= \left(\frac12 + 1 + \frac16\right)\ S_{\square BCDE} + \frac49\ S_{\triangle ABJ},\\ \frac59\ S_{\triangle ABJ} &= \frac53\ S_{\square BCDE},\\ \frac13\ S_{\triangle ABJ} &= S_{\square BCDE}.\end{align}\]

Štvorec \(BCDE\) tvorí tretinu z obsahu trojuholníka \(ABJ\).